Math 104 Fall 2015

Math 104 (Calculus I) Home Page for Section 002

Instructor: Dennis DeTurck

WWW tip: Click on the "Reload" button to make sure you are seeing the most up to date version of this (or any) page!

ANNOUNCEMENTS:

As of about 1:30pm on Thursday I've uploaded your course grades into the system so you can view them on Penn in Touch. Taking advantage of extra credit opportunities definitely helped in a few cases.
Gus, Cole, Jack and I have really enjoyed teaching you this semester. We wish you safe travels, fun holidays and a terrific winter break. See you next year!
Here is the scale on the final exam (agreed upon by all the Math 104 instructors):
- A/A- : 121-150
- B+/B/B- : 91-120
- C+/C/C- : 51-90
We had no "scores of particular concern". As a group, you did well enough that I was able to adjust the scales on the midterms; see below under "Exam info" for the updated scales for those. I'll be getting to work on the course grades this evening, once I've got all of the other grades (homework, extra credit, etc) together.
You guys pretty much rocked the final exam! I'll be posting the final exam scores on Canvas later this morning, but fully 44% of you scored above the A/B cutoff. That has enabled me to adjust the scoring on the midterms, as indicated below.
What a good-looking class!!

Info pages for undergraduate math:

General Information for my section:

Class meetings are Tuesdays and Thursdays from 10:30-12:00 in DRL A1

Recitation sections:
- Mr. Beane's sections:
  - Section 211 - Mondays 8:00-9:00 a.m. in DRL 2C4
  - Section 212 - Mondays 9:00-10:00 a.m. in DRL 2C4
  - Section 213 - Wednesdays 8:00-9:00 a.m. in DRL 4C4
  - Section 214 - Wednesdays 9:00-10:00 a.m. in LRSM 112B
- Mr. Horwitz's sections:
  - Section 215 - Mondays 8:00-9:00 a.m. in DRL 2C2
  - Section 216 - Mondays 9:00-10:00 a.m. in DRL 2C2
  - Section 217 - Wednesdays 8:00-9:00 a.m. in DRL 2C6
  - Section 218 - Wednesdays 9:00-10:00 a.m. in DRL 2C6
- Mr. Gindi's sections:
  - Section 219 - Mondays 6:00-7:00 p.m. in DRL A5
  - Section 220 - Mondays 7:00-8:00 p.m. in DRL A5
Since I am the Dean of the College of Arts and Sciences, I have two offices. I spend most of my time in my "Dean's office", 120 Claudia Cohen Hall (tel. 8-7867). I also have a Math Department office, DRL 3E5D, tel. 3-9036, but I will never be there because the office is being used this semester by a visitor to the department. I'm also faculty director of Riepe College House in the Quad, where I reside in Magee 209. My email address is deturck@sas.upenn.edu.
I will have "regular" office hours on Tuesdays from 6-7:30 pm, at my place in the Quad, since that's a pretty central location. "Regular" means that during those times, I'm there for my Math 104 students, and I'm not allowed to tell you I'm busy (unless it's with another student). There will be other times that I will announce either in class or by email (and they'll always be posted on this website). You are welcome to stop by at other times (during the day usually in Cohen Hall or in the evening or on weekends in Riepe), but at those times I reserve the right to ask you to come back later if I'm involved with other stuff.
The teaching assistants for the course are Gus (Angus) Beane, Cole Hurwitz, and Jack Gindi.
Gus will have office hours on Tuesdays from 3-4pm and Wednesdays from 6-7pm in DRL 4C9. Cole's office hours will be Mondays and Wednesdays from 7-8pm in DRL 3W8. We'll announce Jack's office hours soon.

Basic Ground Rules:

Final grade based on six equal parts: Final exam (equals two parts), three midterm exams, everything else. Everything else includes regular homework, computer homework, the occasional quiz in recitation, lecture points, etc..

Homework will be assigned before each Thursday, and will be due at Thursday's lecture the following week. You will sometimes need to use a computer to do some of your homework. The course will also have a MyMathLab site that you will need to use to turn in some of your homework (after the first one. To get started using MyMathLab with the licence you got with your textbook, download this link to get started.

Homework will contain instructions for reading. Make sure you do the reading before the class for which it is assigned. I will assume you have done so.

Grading notes: At the end of the semester, everyone who has not withdrawn from the class will get a grade. Incompletes will not be given to avoid F's.

LATE WORK will NEVER be accepted.

Exams:

First midterm: Tuesday, September 27 (Review and Chapter 6)
- Practice problems for the first midterm, including last year's midterm, the 2014 midterm and forty (or so) more problems.
- And here are the answers.
- Here is the adjusted scale for the first midterm:
  - A/A- : ~~86-100~~ 83-100
  - B+/B/B- : ~~72-85~~ 65-82
  - C+/C/C- : ~~54-71~~ 45-64
  Scores of 45 30 or below are of particular concern.
Second midterm: Thurssday, October 27 (Chapter 8, Chapter 9 (and section 7.2))
- Here are (lots of) practice problems for the second exam. And the answers.
- As promised, The 80 extra integrals
- Answers to: 1-10, 11-20, 21-30 31-40 41-50 51-62 63-67 68-75 76-80.
- Here is the adjusted scale for the second midterm:
  - A/A- : ~~75-100~~ 72-100
  - B+/B/B- : ~~59-74~~ 56-71
  - C+/C/C- : ~~45-58~~ 35-55
  Scores of 40 30 or below are of particular concern.
Third midterm: Tuesday, December 6 (Chapter 10)
- Here are some practice problems for the third midterm // and the answers.
- Additional review: Rimmer's Fall 15 Midterm 4. (answers)
- Here is the adjusted scale for the third midterm:
  - A/A- : 108-120 this didn't change because you did so well on the third exam
  - B+/B/B- : ~~96-107~~ 93-107
  - C+/C/C- : ~~75-95~~ 70-92
  Scores of 65 60 or below are of particular concern.
Final exam: Monday, December 19, 9-11 am in CHEM 102.
- Here is the final exam from Fall 2015 (which is missing from the collection of old finals on the main Math 104 page). I think the answers are EDC[DCDC]D | FACFE | BCADB.
- Several of you have asked about the answers to the Fall 13 exam. I think they are CBCBA | AAECE | FCJCD (but I worked them very quickly)
- Additionally, here are some practice problems for the final exam (actually, a lot of problems).
- And here are hints and answers to some of the practice problems.
- More material for review: All the midterms from the other sections:
  - Rimmer: Midterm 1 (answers) Midterm 2 (answers) Midterm 3 (answers)
  - Stovall: Midterm 1 (answers) Midterm 2 (answers) Midterm 3 (answers)
  - Palvannan: Midterm 1 (answers) Midterm 2 (answers) Midterm 3 (answers)
  - Gressman: Midterm 1 (answers) Midterm 2 (answers) Midterm 3 (answers)
  - And here are all of the midterms from our class (answers at the end).
- Problems that are particularly good for review (I'm not exactly saying that you can ignore all the other ones, but...)
  - Stovall
    - MT1: 2, 4
    - MT2: 2, 3, 4, 5, 7, 8
    - MT3: 1, 2, 3, 4, 5, 6, 7
  - Rimmer:
    - MT1: 2, 3
    - MT2: 1, 2, 4, 6, 7
    - MT3: 3, 4, 5, 6
  - Gressman
    - MT1: 2, 5, 6, 7, 8, 9, 10, 11
    - MT2: 3, 7, 8, 12
    - MT3: 1, 2, 4, 5, 6, 7, 10, 11
  - Palvannan
    - MT1: 1, 2, 3, 4
    - MT2: 2, 5
    - MT3: 2, 3, 4
  - DeTurck
    - MT1: 3, 4, 8, 9
    - MT2: 1, 2, 3, 4, 5, 7, 10
    - MT3: 1, 2, 3, 5, 6, 9, 10
  - Fall 15 final: 1, 2, 3, 4, 6, 7, 8, 12, 13, 14, 15
  - Fall 14 final: 2, 3, 4, 5, 7, 8, 9, 10, 11, 14
  - Fall 13 final: 1, 3, 4, 5, 6, 7, 10, 11, 13
  - Fall 12 final: 3, 5, 6, 7, 8, 9, 10, 11, 12, 15
  - Practice problems for final: 2, 3, 5, 8, 9, 12, 13, 14, 15, 16, 18(abc)
  - PPs for Exam 3: 1, 2, 3, 4, 8, 9, 13, 17, 19, 21, 22, 23, 25, 27, 29, 30, 31, 33, 34, 35, 36, 37, 39, 41, 43, 44, 46, 1, 2, 3, 4, 6, 8, 9, 2, 3, 6, 8, 9, 1, 3, 4, 6, 9, 10
  - PPs for Exam 2: 2, 3, 6, 7, 11, 12, 13, 14, 15, 17, 18, 20, 22, 25, 28, 1, 2, 3, 6, 7, 9, 10, 2, 3, 5, 6, 7, 9
  - PPs for Exam 1: 3, 4, 8, 9, 10, 3, 4, 8, 1, 4, 6, 12, 14, 17, 21, 23, 25, 28, 29, 32, 35, 36, 38

Ways to get help:

Math Centers
The Tutoring Center - check out their (free!) "Satellite Centers", and
Math 104 Start-Up Workshops

Class notes:

August 30 -- Review of limits and derivatives
September 6 -- Integrals, areas and volumes (typos fixed, 9/8)
Some additional notes on integration:
- Substitution in integrals
- Acceleration/velocity/position problems
- Notes on surfaces of revolution with better (moving) pictures than on the powerpoint slides.
September 29 -- Methods of integration (typos we found on Tuesday morning have been corrected)
October 11 -- Improper integrals
In case it is useful: a table of values for the (standard) normal distribution.
Solution to the October 11 worksheet
October 13 - Differential Equations
November 1 - Sequences and series
Cole's flowchart and some good practice problems on convergence/divergence.
November 10 - Power series / Taylor series

Homework and class notes:

To get or use your MyMathLab licence for homework starting next week, download this link to get started.
August 30 (with assignment 1 and bonus problem 1)
- A couple of you asked about these: Answers to the Fall 03 exam:
  1. A; 2. D; 3. C,F; 4. C; 5. F; 6. E; 7. A; 8. C; 9. E; 10. B; 11. C; 12. 14 (which is not one of the answers); 13. E; 14. B; 15. B
September 6 (Assignment 2 and Bonus problem 2)
September 15 (Assignment 3 and Bonus problem 3)
September 27 (Assignment 4 and Bonus problem 4)
Here are 80 extra integrals to practice on. And answers to 1-10, 11-20, 21-30, 31-40 41-50, 51-62, 63-67
October 11 (Assignment 5 and Bonus problem 5)
October 18 (Assignment 6 and Bonus problem 6)
November 1 (Assignment 7 and Bonus problem 7)
Extra credit project (due Tuesday November 8).
November 8 (Assignment 8 and Bonus problem 8)
November 17 (Assignment 9 and Bonus problem 9) --- Last one!

Bonus problems and solutions:

Bonus problem #1: Suppose that three points on the parabola y = x² have the property that their normal lines intersect at a common point. Show that the sum of their x-coordinates is 0. Is this if and only if?
Solution to Bonus Problem 1 (based on solutions by Sharon Christner and Christopher Lee).
Bonus problem #2: Let ABC be a right-angled triangle with angle ABC = 90 degrees (so the right angle is at vertex B), and let D be the point on side AB such that AD = 2DB. What is the maximum possible value of angle ACD? (Hint: This is a max-min problem, and the first hard thing is to figure out what the variables are!)
- Solution to Bonus Problem 2 (based on the elegant solutions by Michal Kolakowski and Christeen Samuel).
Bonus problem #3: Consider a square with side length L. Let R be the region inside the square consisiting of all points that are closer to the center of the square than to any side of the square. What is the area of R ?
This is an interesting problem -- the hard part is to draw a good picture of the region and get equations for its (curved) sides. (Can you do it with Maple or other software?)
- Solution to Bonus Problem 3 (based on solutions by Eric Teichner, Christeen Samuel and Nina-Simone Lobban).
Bonus problem #4: A cylindrical glass of radius r and height L is filled with water and then tilted until the water remaining in the glass exactly covers its base.
- (a) Determine a way to "slice" the water into parallel rectangular cross sections and then set up a definite integral for the volume of the water in the glass.
- (b) Determine a way to "slice" the water into parallel cross-sections that are trapezoids and then set up a definite integral for the volume of the water.
- (c) Find the volume of water in the glass by evaluating one of the integrals in part (a) or part (b).
- (d) Find the volume of water in the glass from purely geometric considerations.
- (e) Suppose the glass is tilted until the water covers half the base. In what direction can you "slice" the water into triangular cross sections? Rectangular cross-sections? Cross-sections that are segments of circles? Find the volume of water in the glass.
- Here are two pictures that may help:
Bonus problem #5:
- Solution to Bonus Problem 5 (based on solutions by Eric Teichner and Nina-Simone Lobban).
Bonus problem #6:
Prove that (explain why) log₃(11) is an irrational number.
- Here is a solution based on the solutions of Namita Saraf and Andrej Patoski:
  Suppose log₃(11) = r
  where r = a/b, and a and b are both (nonzero) integers (this would define r as a rational number.) Then
  log₃(11) = a/b
  b log₃(11) = a
  log₃(11^b) = a
  3^a = 11^b
  So, for log₃(11) to be a rational number, there must exist nonzero integers a and an integer b for which the above statement is true. Because the prime factorization of any number is different from that of any other number, and 3^a and 11^b are examples of numbers that have been simplified to their prime factors, there cannot be positive integers a and b for which 3^a = 11^b, and so log₃(11) cannot be a rational number.
  Therefore, log₃(11) is an irrational number.
Bonus problem #7:
Find the sum of the series:
1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + 1/16 + 1/18 + ...
where the terms are the reciprocals of the positive integers whose only prime factors are 2s and 3s.
Bonus problem #8:
Consider the series whose terms are the reciprocals of the positive integers that can be written (in ordinary base 10 notation) without using the digit 0. Show that this seris is convergent and that its sum is less than 90.
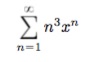Bonus problem #9: Find the interval of convergence of and find its sum.
Bonus problem #10: Does the series for arcsin (derived in the last set of notes) converge or diverge when x = 1 ?