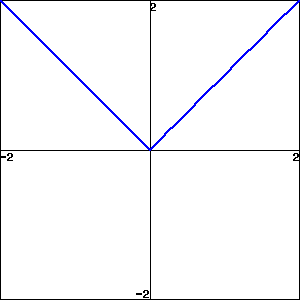
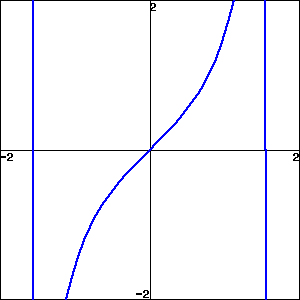
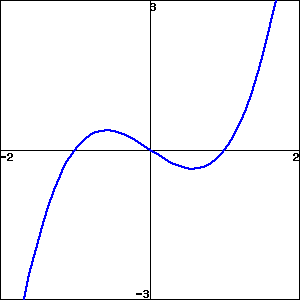
What does the hiker’s landscape look like if \(f'\) is negative to the left of the value \(x=a\) and positive to the right?
Unit 3.3 First and second derivatives, and sketching
Knowledge of the derivative can help you sketch a function more accurately. The very first practice problem asked you to incorporate slope information into a sketch. Sketching is as much an art as a science, but there are methodical ways to use information about the function and its derivatives.
To begin with, knowing where the derivative is positive and negative determines whether it is sloping up or down as you move right. In other words, the sign of the derivative indicates whether the function is increasing or decreasing. Where the sign of the derivative changes from positive to negative as you move right, the function changes from increasing to decreasing. That means someone hiking on the graph of the function from left to right has been walking upwards and now begins to walk downward; see Figure 3.7.
Checkpoint 69.
Because transitions in the sign of \(f'\) correspond to hilltops and valley floors, finding values of \(x\) that are maxima and minima for \(f(x)\) involves finding values of \(x\) for which \(f'(x) = 0\text{.}\) We discuss this at greater length in Chapter 7. For the purposes of sketching, the moral of the story is: know where \(f'\) is positive and where it is negative, and use this to depict a function that is increasing and decreasing in the right places.
Checkpoint 70.
Sketch the graph of a function \(f\) such that \(f'\) is positive when \(x \lt 1\text{,}\) dips to zero at \(x=1\text{,}\) is positive again until \(x=3\text{,}\) is zero at \(x=3\text{,}\) and is negative to the right of \(x=3\text{.}\) See if you can also make \(f\) have a unique zero at \(x = -2\text{.}\)
The second derivative.
A Japanese proverb says, "The other side also has another side." The function \(f\) has a derivative. \(f'\) is also a function. Therefore, The derivative also has a derivative. Not quite so poetic, but very useful for sketching functions. The derivative of the derivative is called the second derivative, denoted \(f''\text{,}\) or \(\frac{d^2 \, f}{dx^2}\text{.}\) The sign of the derivative says where a function is increasing or decreasing, therefore the sign of \(f''\) indicates where the slope \(f'\) is increasing or decreasing. We use italics here as a visual reminder that there are a number of levels (original function, first derivative, second derivative) and attributes (positive/negative, increasing/decreasing) and it’s easy to get mixed up what corresponds to what. We hope Table 3.8 helps clarify whose positivity says what about whom.
| \(f''\) is | \(f'\) is | \(f\) is | graph of \(f\) |
| positive | increasing | of increasing slope | concave upward |
| negative | decreasing | of decreasing slope | concave downward |
| positive | increasing | upward | |
| negative | decreasing | downward | |
| positive | above the horizontal axis | ||
| negative | below the horizontal axis |
Remark 3.9.
The placement of the 2 in the numerator of \(\frac{d^2 \, f}{dx^2}\) may seem strange, but it reflects something important: \((d/dx)\) is a differential operator, and \((d^2 / dx^2)\) is the result of applying this operator twice. This becomes important in later courses such as MATH 1410.
Of course, not every function is differentiable, and not every derivative is itself differentiable, so \(f''\) may not exist even if \(f'\) exists.
We have talked informally about functions that are concave up or down. It is time to give a definition. In fact we give two definitions, one algebraic and one pictorial. The pictorial one is in fact more general because it works when \(f'\) does not exist. When \(f'\) exists on \((a,b)\text{,}\) then the two definitions agree.
Definition 3.10. concavity.
Definition 3.11. concavity (pictorial definition).
If \((a,b)\) is an open interval in the domain of \(f\) and if for every pair of numbers \(x,y \in (a,b)\)the graph of \(f\)on \((a,b)\) lies below the line segment connecting \((x,f(x))\)to \((y,f(y))\text{,}\) we say that \(f\) is concave upward on \((a,b)\text{.}\)
Checkpoint 72.
To summarize, if \(f''\) exists on \((a,b)\) then the sign of \(f''\) determines the concavity of \(f\text{.}\) If \(f''\) doesn’t exist or you can’t compute it, use Definition 3.10.
Points of inflection.
We never formally defined a tangent line. One definition would be "A line that touches a graph of a function at precisely one point and stays on one side of the graph other than this."
Checkpoint 73.
Here are four ways this definition may fail to capture what some people think a tangent line should be. For each example, please say whether you think the given line ought to count as a “tangent line.”
-
Graph of \(y = |x|\text{;}\) any line with absolute slope less than 1.
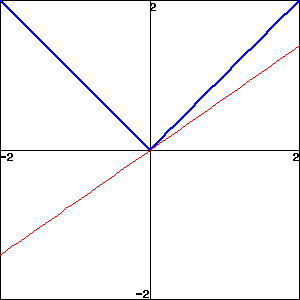
-
Graph of \(y = \tan x\text{;}\) line of slope 1 through the origin.
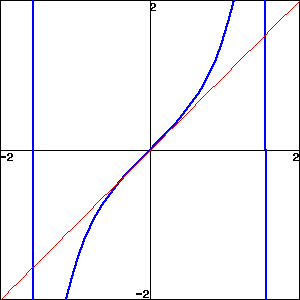
-
Graph of a cubic with a tangent line that intersects the cubic elsewhere.
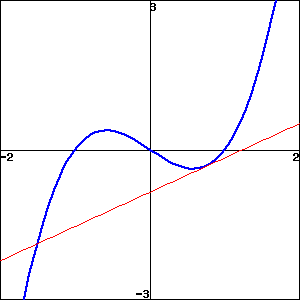
-
Graph with a vertical cusp.
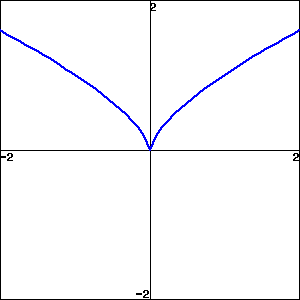
As you can see, the intuitive definition of tangent line is subject to unanticipated judgment calls. This motivates a more formal definition.
Definition 3.12. tangent line.
If \(f\) is differentiable at \(a\text{,}\) the tangent line to \(f\) at \(a\) is defined to be the line \((y-f(a)) = m (x-a)\) where \(m = f'(a)\text{.}\)
Checkpoint 74.
One confusing case is when the second derivative is zero. What happens to the concavity at such a point? Often it switches from up to down or vice versa. Wherever concavity switches is called a point of inflection. The geometric concept of an inflection point does not require calculus, though the notion seems not to have been discussed much before the advent of calculus.
Checkpoint 75.
Checkpoint 76.
-
Sketch a graph of the sine function.
-
Mark the intervals where sine increases and those where it decreases.
-
On the same graph sketch the cosine function.
-
The derivative of \(\sin\) is \(\cos\text{;}\) what does this imply about the values of cosine on the marked intervals?
-
Where are the points of inflection for sine and what happens to the cosine at those arguments?