Example 8.1.
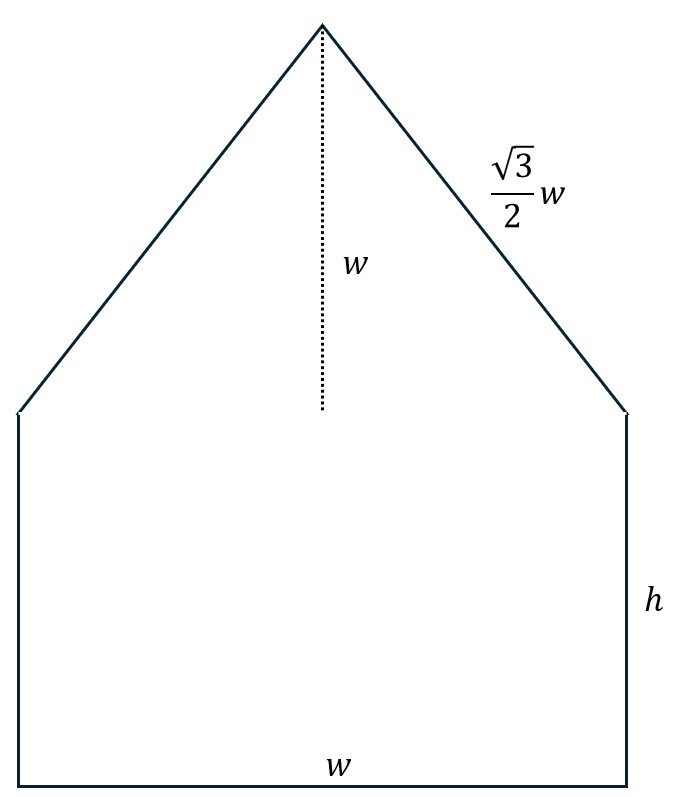
We’re going to build a window in the shape of a rectangle topped by an isosceles triangle whose height is the same as the width of the rectangular portion. We want to make a window which lets in the most light -- that is, with the greatest possible area. In order to build the window, we have to use wood trim. We have 16 feet of wood trim to build the window with.
Such a window has two dimensions: the width \(w\) and the height \(h\) of the rectangle. The rectangular portion has area \(wh\) and the triangular portion has area \(\frac{1}{2}w^2\text{.}\) So the total area is
\begin{equation*}
A(w,h)=wh+\frac{1}{2}w^2\ .
\end{equation*}
We also need to record the fact that our supplies are limited. A little geometry shows that to build the window requires two pieces of trim with length \(h\text{,}\) two of length \(w\text{,}\) and two of length \(\frac{\sqrt{3}}{2}w\text{.}\)
Technically we don’t have to use all the trim, but if we had some left over, we could have used it to build a bigger window. So let’s assume we use all 16 feet; that is, we assume
\begin{equation*}
16=2h+2\left(1+\frac{\sqrt{3}}{2}\right)w\ .
\end{equation*}
We can solve this equation for either \(w\) or \(h\text{.}\) Let’s solve for \(h\text{:}\)
\begin{equation*}
h=8-\left(1+\frac{\sqrt{3}}{2}\right)w
\end{equation*}
and substitute that into the formula for area:
\begin{equation*}
A(w,h(w))=w\left(8-\left(1+\frac{\sqrt{3}}{2}\right)w\right)+\frac{1}{2}w^2
\end{equation*}
Now we’ve got a function which we can optimize. We want to have a sensible result, so we know that \(w\) can’t be less than 0, and can be at most \(\frac{8}{1+\frac{\sqrt{3}}{2}}\text{.}\) So we want to optimize on the interval \(\left[0,\frac{8}{1+\frac{\sqrt{3}}{2}}\right]\text{.}\)
Differentiating, we get \(\frac{dA}{dw}=8-\left(1+\sqrt{3}\right)w\text{.}\) So there is a single critical point at \(w=\frac{8}{1+\sqrt{3}}\text{.}\) We have
\begin{gather*}
A(0,h(0))=0\\
A\left(\frac{8}{1+\frac{\sqrt{3}}{2}},h\left(\frac{8}{1+\frac{\sqrt{3}}{2}}\right)\right)=A\left(\frac{8}{1+\frac{\sqrt{3}}{2}},0\right)=\frac{1}{2}\left(\frac{8}{1+\frac{\sqrt{3}}{2}}\right)^2=\frac{128}{\left(2+\sqrt{3}\right)^2}\\
A\left(\frac{8}{1+\sqrt{3}},h\left(8+\sqrt{3}\right)\right)=\frac{32}{1+\sqrt{3}}
\end{gather*}
Since \(\frac{32}{1+\sqrt{3}}\approx 11.71\) is greater than either 0 or \(\frac{128}{\left(2+\sqrt{3}\right)^2}\approx 9.12\text{,}\) we see that the maximal area occurs when we choose \(w=\frac{8}{1+\sqrt{3}}\) and \(h=h(\frac{8}{1+\sqrt{3}})=\frac{8}{1+\sqrt{3}}\frac{\sqrt{3}}{2}\text{.}\)