Unit 2 Bounding
To get an upper bound on \(f(x)\) means to find a quantity \(U(x)\) that you understand better than \(f (x)\) and for which you can prove that \(U(x) \geq f(x)\text{.}\) A lower bound is a quantity \(L(x)\) that you understand better than \(f(x)\) and that you can prove to satisfy \(L(x) \leq f(x)\text{.}\) If you have both a lower and upper bound, then \(f(x)\) is stuck for certain in the interval \([L(x),U(x)]\text{.}\)
Checkpoint 3.
Aside
While estimating produces statements that are not mathematically well defined, bounding produces inequalities with precise mathematical meaning. Two ways we typically find bounds are as follows.
First, if \(f\) is monotone increasing then an easy upper bound for \(f(x)\) is \(f(u)\) for any \(u \geq x\) for which we can compute \(f(u)\text{.}\) Similarly an easy lower bound is \(f(v)\) for any \(v \leq x\) for which we can compute \(f(v)\text{.}\) If \(f\) is monotone decreasing, you can swap the roles of \(u\) and \(v\) in finding upper and lower bounds. There are even stupider bounds that are still useful, such as \(f(x) \leq C\) if \(f\) is a function that never gets above \(C\text{.}\)
Example 2.6.
Suppose we wanted to estimate \(\sin (1)\text{.}\) The easiest upper and lower bounds are \(1\) and \(-1\) respectively because \(\sin\) never goes above \(1\) or below \(-1\text{.}\) A better lower bound is \(0\) because \(\sin (x)\) remains positive until \(x=\pi/2\) and obviously \(1 \lt \pi/2\text{.}\) You might in fact recall that one radian is just a bit under \(60^\circ\text{,}\) meaning that \(\sin (60^\circ) = \sqrt{3}/2
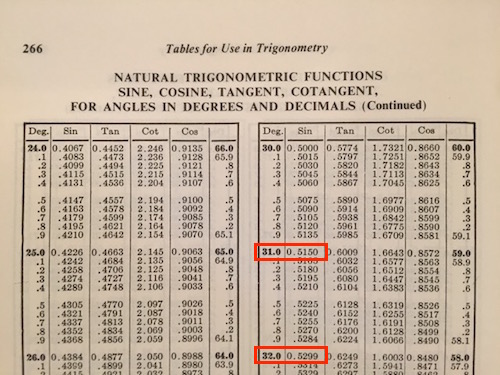
\approx 0.0866\ldots\) is an upper bound for \(\sin (1)\text{.}\) Computing more carefully, we find that a radian is also less than \(58^\circ\text{.}\) Is \(\sin (58^\circ)\) a better upper bound? Probably not: we don’t know how to calculate it, so it’s not a quantity we understand better. Of course if we had an old-fashioned table of sines,
and all we can remember about one radian is that it is between \(57^\circ\) and \(58^\circ\text{,}\) then \(\sin (58^\circ)\) is not only an upper bound but the best one we have.
Aside