The sum rule, in an applied setting, says something like this. Suppose Dick’s net worth at time \(t\text{,}\) call it \(f(t)\text{,}\) is increasing at a certain rate, and Jane’s, call it \(g(t)\text{,}\) is increasing at another rate. Then their joint fortune (they are married) is increasing at a rate that is the sum of the two individual rates. Stated in these terms, is the sum rule obvious or does it require proof?
Unit 4.2 Arguments and proofs
Proofs are for convincing others, as well as for deciding whether you know something for sure, in all cases. The next two exercises ask for opinions on whether or not a proof is needed. There’s no right answer, but we expect you to give a good sense of why or why not.
Checkpoint 86. the sum rule: obvious or not?
Checkpoint 87. the chain rule: obvious or not?
In applied terms, suppose \(f(t)\) is the length in meters of a turtle that is \(t\) days old and \(g(t) = 3.3 f(t)\) is the length in feet. Then \(g'(t)\text{,}\) the rate of increase of length in feet per day, should be 3.3 times \(f'(t)\text{,}\) the rate of increase in meters per day. Obvious or not?
In case some of you answered that it was not obvious, here is a mathematical proof. In most of the upcoming proofs, we need to use the definition of the derivative as a limit of difference quotients. We don’t need to use the \(\varepsilon\)-\(\delta\) definition of limit, just known facts about limits.
Let \(h = f+g\text{.}\) By definition
\begin{equation*}
h'(a) = \lim_{x \to a} \frac{h(x) - h(a)}{x-a}
= \lim_{x \to a} \frac{(f(x) + g(x)) - (f(a) + g(a))}{x-a} \,
\end{equation*}
The difference quotient on the right-hand side simplifies to \(\frac{f(x) - f(a)}{x-a} + \frac{g(x) - g(a)}{x-a} \, .\) This is a sum of two things. The limit of the sum is the sum of limits, therefore
\begin{equation*}
h'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x-a}
+ \lim_{x \to a} \frac{g(x) - g(a)}{x-a} = f'(a) + g'(a) \,
\end{equation*}
As you can see, the logic broke this down into small steps, justified by facts we have accumulated. The proof didn’t add a whole lot to our understanding, although it does help to nail down the fact that this holds whenever \(f'(a)\) and \(g'(a)\) exist, without exceptions for when one of them is zero, or undefined for values other than \(a\text{,}\) or anything like that.
We’ll ask you to do one of these on your own, then not bother you with proofs of things that are borderline obvious.
Checkpoint 88.
Prove Proposition 4.3. It’s pretty similar to the proof for the sum rule but a little easier.
A close up look at the product rule.
We mentioned earlier what units a derivative has, but never discussed why. Now is a good time. Taking the limit of an expression gives something with the same units. The derivative is the limit of a difference quotient \((f(x+h) - f(x)) / h\text{.}\) The numerator is the difference between two things with the same units, namely the units of the value of \(f\text{.}\) The denominator has units of the argument of \(f\text{.}\) So the difference quotient has units of the value of \(f\) divided by the argument of \(f\text{.}\) For example, if \(f(t)\) is distance traveled in the time \(t\text{,}\) then \(f'\) has units of distance per time (such as MPH).
Why is \((fg)'\) not equal to \(f' g'\text{?}\) There are many reasons, one of which is the units. In an application, the values of \(f\) and \(g\) might have different units, but if both are being differentiated with respect to \(x\) then they must have the same input units. The units of \((fg)'\) are, as we have just seen, units of \(f\) times units of \(g\) divided by units of \(x\text{,}\) the argument. Unfortunately \(f' g'\) has the units of \(f/x\) times the units of \(g/x\text{,}\) so one too many units of \(x\) in the denominator.
We now present three arguments for the product rule. When we’re done, we’ll take a poll of which is most convincing.
If \(f\) is a constant, so all the change in the product \(fg\) comes from changes in \(g\text{,}\) then we have seen \((fg)' = f \cdot g'\text{.}\) If \(g\) is a constant, then similarly, \((fg)' = g f'\text{.}\) In reality, both are changing, so the rate of change of the area is the sum of these two individual rates.
Suppose \(f(t)\) is the length in meters of a growing rectangular blob at time \(t\) seconds, and \(g(t)\) is its width. How fast is the area growing at time \(t\text{?}\)

Figure 4.10 shows the classical pictorial argument. When time increases by a small quantity \(\Delta t\text{,}\) both \(f\) and \(g\) increase by small quantities, which we respectively call \(\Delta f\) and \(\Delta g\text{,}\) and the area increases by \(f \Delta g\) plus \(g \Delta f\) plus \((\Delta f) (\Delta g)\text{.}\) We know that \(\Delta f\) is approximately \(f'(t) \Delta t\text{,}\) because in the limit as \(\Delta t \to 0\text{,}\) the ratio \(\Delta f / \Delta t\) converges to \(f'(t)\text{.}\) Similarly, \(\Delta g \approx g'(t) \Delta t\text{.}\) From the picture, you can see that \(\Delta (fg) = f \Delta g + g \Delta f
+ (\Delta g) (\Delta f)\text{.}\) So
\begin{equation*}
\frac{\Delta fg}{\Delta t} = f \frac{\Delta g}{\Delta t}
+ g \frac{\Delta f}{\Delta t}
+ \frac{(\Delta f) (\Delta g)}{\Delta t} \,
\end{equation*}
Taking limits on the right hand side as \(\Delta t \to 0\) gives \(f' g + g' f + \lim_{\Delta t \to 0} (\Delta f)(\Delta g) / \Delta t\text{.}\) This last limit should be zero. Why? Say \(f'(t) = a\) and \(g'(t) = b\text{.}\) Then \(\Delta f \approx a \Delta t\) and \(\Delta g \approx b \Delta t\text{,}\) so
\begin{equation*}
\displaystyle\lim_{\Delta t \to 0} \frac{(\Delta f)(\Delta g)}{\Delta t}
\approx
\lim_{\Delta t \to 0} \frac{f'(t) (\Delta t) g'(t) (\Delta t)}{\Delta t}
= \lim_{\Delta t \to 0} f'(t) g'(t) (\Delta t)
\end{equation*}
which is zero.
Aside
The simplest algebraic proof of the product rule is a bit more out of the blue because it relies on this trick:
\begin{equation*}
f(x+h) g(x+h) - f(x) g(x) = f(x+h) g(x+h) - f(x+h) g(x)
+ f(x+h) g(x) - f(x) g(x)
\end{equation*}
and hence
\begin{equation*}
\frac{f(x+h) g(x+h) - f(x) g(x)}{h} = f(x+h) \frac{g(x+h) - g(x)}{h}
+ g(x) \frac{f(x+h) - f(x)}{h} \,
\end{equation*}
The trick was, we added and subtracted \(f(x+h) g(x)\) in order to be able to separate the original difference quotient into two pieces, each of which looks like a function times a simpler difference quotient. Taking limits and using the fact that limits of sums are sums of limits, and the same for products, gives
\begin{align*}
(fg)'(x) & = \lim_{h \to 0} \frac{f(x+h) g(x+h) - f(x) g(x)}{h} \\
& = \lim_{h \to 0} f(x+h) \frac{g(x+h) - g(x)}{h}
+ \lim_{h \to 0} g(x) \frac{f(x+h) - f(x)}{h} \\
& = \lim_{h \to 0} f(x+h) \lim_{h \to 0} \frac{g(x+h) - g(x)}{h}
+ \lim_{h \to 0} g(x) \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \\
& = f(x) g'(x) + g(x) f'(x)
\end{align*}
Checkpoint 89.
Because \(f\) and \(g\) are differentiable, they are continuous (see Checkpoint 52 and Checkpoint 104). The formal proof above uses that fact that one of the two is continuous at \(x\) but does not use continuity of the other. Which continuity fact is needed?
-
We use the fact that \(f\) is continuous.
-
We use that \(g\) is continuous.
-
We use that both are continuous.
-
We don’t need to use continuity of either function.
Where is this continuity fact used?
-
To handle \(\lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \text{.}\)
-
To handle \(\lim_{h\rightarrow 0}\frac{g(x+h) - g(x)}{h}\text{.}\)
-
To handle \(\lim_{h\rightarrow 0}f(x+h)\text{.}\)
-
To handle \(\lim_{h \to 0} g(x)\text{.}\)
A physics proof of the derivative of the sine function.
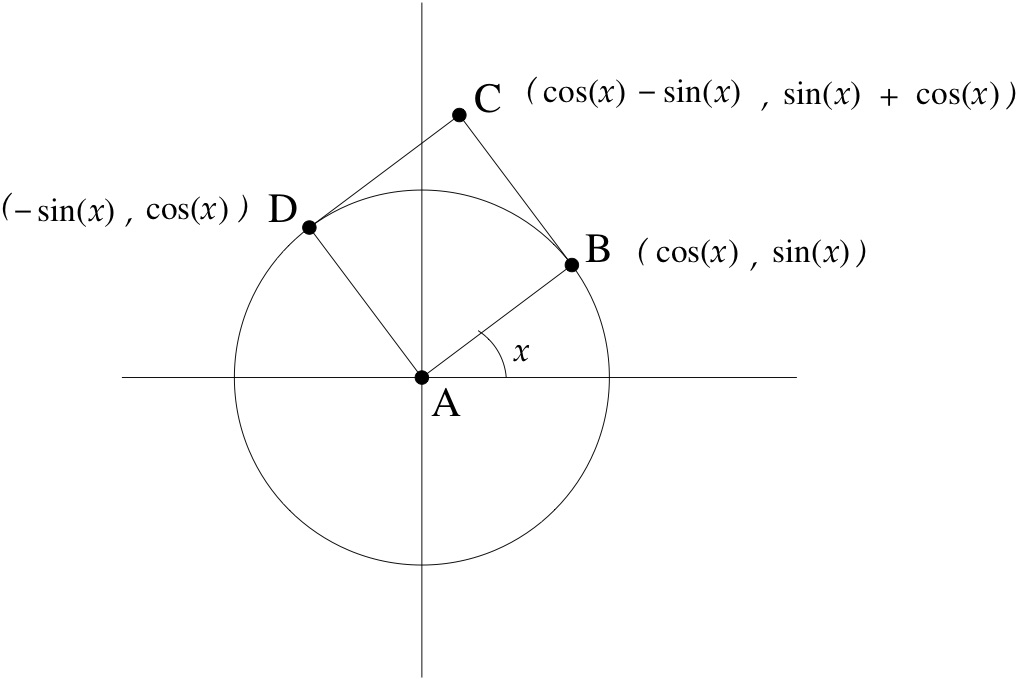
Suppose a toy car is moving around a circular track of radius one meter, so that its speed is constant 1 meter per second; the coordinates of the point are \(x = \cos t, y = \sin t\text{.}\) By definition of radian, its angle with respect to the horizontal increases at a rate of one radian per second. The northward (\(y\)-direction) speed is the derivative of \(\sin t\text{.}\) Suppose at time \(x\) a gate opens up and the car stops turning to stay on the track and coasts straight onward at its present speed of 1. Its northward speed during the time \([x,x+1]\) is the derivative of the sine function at time \(x\text{.}\) To evaluate this, we just have to check how far northward the car went from time \(x\) to \(x+1\text{.}\) This is just analytic geometry. The car goes one unit tangent to the circle during this time interval from the point \((\cos x , \sin x)\) (B in Figure 4.11) to the point \((\cos t - \sin t, \sin t + \cos t)\) (A in the figure). Therefore the derivative of \(\sin\) is \(\cos\text{.}\) For free, we also get (by looking at the \(x\) coordinate) that the derivative of \(\cos\) is \(-\sin\text{.}\)
The chain rule.
The easiest way to make sense of the chain rule is in terms of related rates. Think of \(x, u\) and \(y\) as physical quantities related by rules. If you change \(x\text{,}\) it changes \(u\text{.}\) The specific rule is \(u = g(x)\text{.}\) If you change \(u\) it changes \(y\text{.}\) The specific rule is \(y = f(u)\text{.}\)

Aside
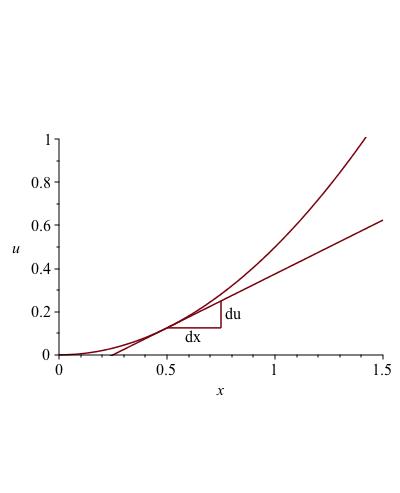
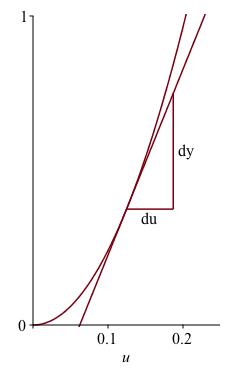
What does this mean quantitatively? The rate of change of \(u\) with respect to \(x\) is \(g'(x)\text{.}\) This is illustrated on the left side of Figure 4.13, where the infinitesimal changes \(dx\) and \(du\) are depicted. The slope of the hypotenuse of the small triangle is \(g'(x)\text{,}\) where in the diagram, the value of \(x\) is roughly \(1/2\text{.}\) On the right side of the figure, we see that this small change in \(u\) leads to a proportionate small change in \(y\text{.}\) The ratio, \(dy/du\) is equal to \(f'(u)\text{.}\) One question remains: at what value of \(u\) is this ratio evaluated? In the figure, it appears \(u \approx 1/8\text{.}\) More precisely, if we originally took \(x\) to be \(1/2\text{,}\) the \(u\) value will be \(f(1/2)\text{.}\) In other words, the value from the \(u\)-axis (vertical in the first graph) is copied to the second graph (where the \(u\)-axis is now the horizontal axis). In other words, \(f'\) is evaluated at \(u\text{,}\) which is \(g(x)\text{.}\) Thus \(dy/dx = du/dx \cdot dy/du |_{u = g(x)}\text{.}\)
If we want to make this into a formal proof, we might start by writing
\begin{equation*}
(f \circ g)' (a) = \lim_{h \to 0} \frac{f(g(a+h)) - f(g(a))}{h} \,
\end{equation*}
If \(g(a+h)\) could be replaced by the tangent line approximation \(g(a) + h g'(a)\) then the proof would finish easily: letting \(\varepsilon :=
h g'(a)\text{,}\)
\begin{equation*}
\displaystyle\lim_{h \to 0} \frac{f(g(a) + h g'(a)) - f(g(a))}{h}
= \lim_{\varepsilon \to 0} \frac{f(g(a) + \varepsilon) - f(g(a))}{(\varepsilon / g'(a))}
= g'(a) f'(g(a)) \,
\end{equation*}
It is indeed true that the tangent line approximation is close enough to \(g\) itself to make this work, but proving that takes a trickier argument than we want to go into here.
