Unit 13 Integrals over the whole real line
Subsection 13.1 Definitions
The situation when integrating out to infinity is similar to the situation with infinite sums. Because there is no already assigned situation with infinite sums. Because there is no already assigned meaning for summing infinitely many things, we defined this as a limit, which in each case needs to be evaluated:
It is the same when one tries to integrate over the whole real line. We define such integrals by integrating over a bigger and bigger piece and taking the limit. In fact the definition is even pickier than that. We only let one of the limits of integration go to zero at a time. Consider first an integral over a half-line \([a,\infty)\text{.}\)
Definition 13.1. one-sided integral to infinity.
Let \(a\) be a real number and let \(f\) be a continuous function on the infinite interval \([a,\infty)\text{.}\) We defineCheckpoint 158.
Write down the defining limit for \(\displaystyle \int_{-\infty}^3 e^x \, dx\) and evaluate the limit.
\(\text{}\)
If we want both limits to be infinite then we require the two parts to be defined separately.
Definition 13.2. two-sided integral to infinity.
Let \(a\) be a real number and Let \(f\) be a continuous function on the whole real line. Pick a real number \(c\) and defineExample 13.3.
What is \(\displaystyle \int_{-\infty}^\infty \frac{x}{x^2 + 1}\text{?}\) Choosing \(c=0\text{,}\) we see it is the sum of two one-sided infinite integrals \(\int_0^\infty x/(x^2+1) \, dx + \int_{-\infty}^0 x/(x^2+1) \, dx\text{.}\) Going back to the definition replaces each one-sided infinite integral by a limit:At this point you should be bothered by three questions.
- What is \(c\text{?}\) Does it matter? How do you pick it?
The answer to the first question is, pick \(c\) to be anything, you'll always get the same answer. This is important because otherwise, what we wrote isn't really a definition. The reason the integral does not depend on \(c\) is that if one changes \(c\) from, say, 3 to 4, then the first of the two integrals loses a piece: \(\int_3^4 f(x) \, dx\text{.}\) But the second integral gains this same piece, so the sum is unchanged. This is true even if one or both pieces is infinite. Adding or subtracting the finite quantity \(\int_3^4 f(x) \, dx\) won't change that.
- If we get \(-\infty + \infty\text{,}\) shouldn't that possibly be something other than "undefined"?
The answer to the second question is yes, sometimes you can be more specific. The one-sided integral to infinity is a limit. Cases where a finite limit does not exist can be resolved into limits of \(\infty\) or \(-\infty\text{,}\) along with the remaining cases where no limit exists even allowing for infinite limits. Because integrals over the whole real line are sums of one-sided (possibly infinite) limits, the rules for infinity from Sections~\ref{ss:variations} and~\ref{ss:LH} can be applied. In other words, integrals over the whole real line are the sum of two one-sided limits; we can add real numbers and \(\pm \infty\) according to the rules in Definition 7.1: \(\infty + \infty = \infty\) (and analogously with \(-\infty\)), \(\infty + a = \infty\) when \(a\) is real (and analogously with \(-\infty\)), \(\infty - \infty = UND\text{,}\) \(UND + {\rm anything } = UND\text{,}\) and so on.
- Why do we have to split it up in the first place?
-
The third question is also a matter of definition. The reason we make the choice to do it this way is illustrated by the integral of the sign function
\begin{equation*} f(x) = {\rm sign} (x) = \left \{ \begin{array}{lr} 1 & x \geq 0 \\ 0 & x=0 \\ -1 & x \lt 0 \end{array} \right. \end{equation*}On one hand, \(\int_{-M}^M f(x) \, dx\) is always zero, because the postive and negative parts exactly cancel. On the other hand, \(\int_M^\infty f(x) \, dx\) and \(\int_{-\infty}^M f(x) \, dx\) are always undefined. Do we want the answer for the whole integral \(\int_{-\infty}^\infty f(x) \, dx\) to be undefined or zero? There is no intrinsically correct choice here but it is a lot safer to have it undefined. If it has a value, one could make a case for values other than zero by centering the integral somewhere else, as in the following exercise.
Checkpoint 159.
Example 13.4.
The function \(\sin(x) / x\) is not defined at \(x=0\) but you might recall it does have a limit at 0, namely \(\lim_{x \to 0} \sin(x) / x = 1\text{.}\) Therefore the function
is a continuous function on the whole real line. Its graph is shown in Figure 13.5.
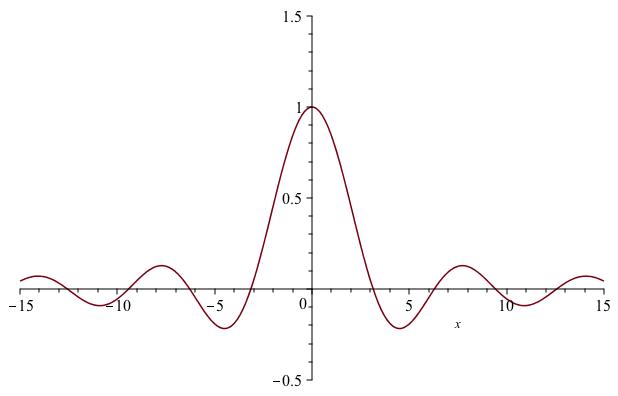
To write down a limit that defines this integral, we first choose any \(c\text{.}\) Choosing \(c=0\) makes things symmetric. The integral is then defined as the sum of two integrals, \(\int_{-\infty}^0 \operatorname{sinc}(x) \, dx + \int_0^{\infty} \operatorname{sinc}(x) \, dx\text{.}\) Going back to the definition of one-sided integrals as limits, this sum of integrals is equal to
It is not obvious whether these limits exist. One thing is easy to discern: because \(\operatorname{sinc}\) is an even function, the two limits have the same value (whether finite or not). We can safely say:
Checkpoint 160.
Subsection 13.2 Convergence
The central question of this section is: how do we tell whether a limit such as \(\int_b^\infty f(x) \, dx\) exists? If the limit exists, we would like to evaluate it if possible, or estimate it otherwise. When discussing convergence you should realize that \(\int_a^\infty f(x) \, dx\) either diverges for all values of \(a\) or converges for all values of \(a\) as long as \(f\) is defined and continuous on \([a,\infty)\text{.}\) For this reason, we use the notation \(\int^\infty f(x) \, dx\) or, to be really blunt, \(\displaystyle \int_{\rm who cares}^\infty f(x) \, dx\text{.}\)
Checkpoint 161.
Case 1: you know how to compute the definite integral.
Suppose \(\int_b^M f(x) \, dx\) is something for which you know how to compute an explicit formula. The formula will have \(M\) in it. You have to evaluate the limit as \(M \to \infty\text{.}\) How do you do that? There is no one way, but that's why we studied limits before. Apply what you know. What about \(b\text{,}\) do you have to take a limit in \(b\) as well? I hope you already knew the answer to that. In this definition, \(b\) is any fixed number. You don't take a limit.
These special cases will become theorems once you have worked them out.
| Name of test | Type of integral | Condition for convergence |
| \(\displaystyle \int_b^\infty e^{kx} \, dx\) | ||
| power test | \(\displaystyle \int_b^\infty x^p \, dx\) | |
| \(\displaystyle \int_b^\infty \frac{(\ln x)^q}{x} \, dx\) |
You will work out these cases in class: write each as a limit, evaluate the limit, state whether it converges, which will depend on the value of the parameter, \(k, p\) or \(q\text{.}\) Go ahead and pencil them in once you've done this. The second of these especially, is worth remembering because it is not obvious until you do the computation where the break should be between convergence and not.
Checkpoint 162.
Work out the first special case: for what real \(k\) does the integral converge?
all \(k\)
\(\displaystyle k\gt 0)\)
\(\displaystyle k\lt 0\)
\(\displaystyle k\gt 1\)
\(\displaystyle k\lt 1\)
something else
\(\text{Choice 3}\)
Case 2: you don't know how to compute the integral.
In this case you can't even get to the point of having a difficult limit to evaluate. So probably you can't evaluate the improper integral. But you can and should still try to answer whether the integral has a finite value versus being undefined. This is where comparison tests come in. You build up a library of cases where you do know the answer and then, for the rest of functions, you try to compare them to functions in your library.
Sometimes a comparison is informative, sometimes it isn't. Suppose that \(f\) and \(g\) are positive functions and \(f (x) \leq g(x)\) for all \(x\text{.}\) Consider several pieces of information you might have about these functions.
| what you know | conclusion | |
| (a) | \(\int_b^\infty f(x) \, dx\) converges to a finite value \(L\text{.}\) | |
| (b) | \(\int_b^\infty f(x) \, dx\) does not converge. | |
| (c) | \(\int_b^\infty g(x) \, dx\) converges to a finite value \(L\text{.}\) | |
| (d) | \(\int_b^\infty g(x) \, dx\) does not converge. |
In which cases can you conclude something about the other function? We are doing this in class. Once you have the answer, either by working it out yourself or from the class discussion, please pencil it in here so you'll have it for later reference.
Checkpoint 163.
Suppose you want to show that \(\displaystyle \int_1^\infty \frac{3 + sin(x)}{x^2} \, dx\) converges. Which pair of facts allows you to do this?
\(\frac{3 + \sin x}{x^2} \geq \frac{2}{x^2}\) and \(\int^\infty \frac{2}{x^2} \, dx\) converges
\(\frac{3 + \sin x}{x^2} \leq \frac{4}{x^2}\) and \(\int^\infty \frac{4}{x^2} \, dx\) does not converge
\(\frac{3 + \sin x}{x^2} \leq \frac{4}{x^2}\) and \(\int^\infty \frac{4}{x^2} \, dx\) converges
\(\frac{3 + \sin x}{x^2} \leq \frac{4}{x^2}\) and \(\int^\infty \frac{2}{x^2} \, dx\) does not converge
\(\text{Choice 3}\)
Asymptotic comparison tests.
Here are two key ideas that help your comparison tests work more of the time, based on the fact that the question "convergent or not?" is not sensitive to certain differences between integrands.
Multiplying by a constant does not change whether an integral converges. That's because if \(\displaystyle \lim_{M \to \infty} \int_b^M f(x) \, dx\) converges to the finite constant \(L\) then \(\displaystyle \lim_{M \to \infty} \int_b^M K f(x) \, dx\) converges to the finite constant \(KL\text{.}\)
Checkpoint 164.
Does \(\displaystyle \int_1^\infty \frac{10}{x} \, dx\) converge or not?
yes, this integral converges.
no, this integral diverges.
If the integral does not converge, is the value \(\infty\) or \(-\infty\) or is it truly undefined?
the integral converges.
the integral diverges to \(-\infty\text{.}\)
the integral diverges to \(\infty\text{.}\)
the integral is 'truly undefined'.
It doesn't matter if \(f(x) \leq g(x)\) for every single \(x\) as long as the inequality is true for sufficiently large \(x\text{.}\) If \(f(x) \leq g(x)\) once \(x \geq 100\text{,}\) then you can apply the comparison test to compare \(\int_b^\infty f(x) \, dx\) to \(\int_b^\infty g(x) \, dx\) as long as \(b \geq 100\text{.}\) But even if not, once you compare \(\int_{100}^\infty f(x) \, dx\) to \(\int_{100}^\infty g(x) \, dx\text{,}\) then adding the finite quantity \(\int_b^{100} f(x) \, dx\) or \(\int_b^{100} g(s) \, dx\) will not change whether either of these converges.
Putting these two ideas together leads to the conclusion that if \(f(x) \leq K g(x)\) from some point onward and \(\int_b^\infty g(x) \, dx\) converges, then so does \(\int_b^\infty f(x) \, dx\text{.}\) The theorem we just proved is:
Theorem 13.8. asymptotic comparison.
If \(f\) and \(g\) are positive functions on some interval \((b,\infty)\) and if there are some constants \(M\) and \(K\) such thatIn particular, if \(f(x) \ll g(x)\) as \(x \to \infty\) then \mathbb{E}qref{eq:O} holds, hence convergence of the integral \(\int_b^\infty g(x) \, dx\) implies convergence of the integral \(\int_b^\infty f(x) \, dx\text{.}\)
Checkpoint 165.
Let \(f(x) := 3x^3 / (x - 17)\) and \(g(x) := x^2\text{.}\) Is it true that \(f(x) \leq K g(x)\) from some point onward?
Yes, if we pick \(K\) large enough, then at some point \(f(x)\) starts being less than \(Kg(x)\) and stays that way.
No. No matter how large we pick \(K\text{,}\) we'll be able to find large \(x\) so that \(f(x)\gt Kg(x)\text{.}\)
\(\text{Choice 1}\)
Example 13.9. power times negative exponential.
Does \(\displaystyle \int_1^\infty x^8 e^{-x} \, dx\) converge? One way to do this is by computing the integral exactly. This takes eight integrations by parts, and is probably too messy unless you figured out how to do "tabular" integration (optional when you learned integration by parts). In any case, there's an easier way if you only want to know whether it converges, but not to what.
We claim that \(x^8 e^{-x} \ll e^{- (1/2) x}\) (you could use \(e^{-\beta x}\) in this argument for any \(\beta \in (0,1)\)). It follows from the asymptotic comparison test that convergence of \(\int_1^\infty e^{-(1/2) x}\) implies convergence of \(\int x^8 e^{-x} \, dx\text{.}\) We check the claim by evaluating
because we know the power \(x^8\) is much less than the exponential \(e^{(1/2) x }\text{.}\)
Checkpoint 166.
A particular case of Theorem 13.8 is when \(f(x) \sim g(x)\text{.}\) When two functions are asymptotically equivalent, then each can be upper bounded by a constant multiple of the other, hence we have the following proposition.
Proposition 13.10.
If \(f\) and \(g\) are positive functions and \(f \sim g\) then \(\int^\infty f(x) \, dx\) converges if and only if \(\int^\infty g(x) \, dx\) converges.Example 13.11.
- Does \(\displaystyle \int_1^\infty \frac{dx}{x^2 + 3x}\) converge?
We can use comparison test (c) here: \(\displaystyle \frac{1}{x_2 + 3x} \leq \frac{1}{x^2}\) and we know \(\displaystyle \int_1^\infty \frac{dx}{x^2}\) converges, hence so does \(\displaystyle \int_1^\infty \frac{dx}{x^2 + 3x}\text{.}\)
- Does \(\displaystyle \int_4^\infty \frac{dx}{x^2 - 3x}\) converge?
Now the inequatlity goes the other way, so we are in case (c) of the comparison test and we cannot conclude anything from direct comparison. However, we also know \(\displaystyle \frac{1}{x^2 - 3x} \sim \frac{1}{x^2}\) as \(x \to \infty\text{,}\) therefore we can conclude convergence again by Proposition 13.10.
Did you wonder about the lower limit of 4 in the second part? That wasn't just randomly added so you'd be more flexible about the lower limits of integrals to infinity. It was put there to ensure that \(f\) was continuous; note the discontinuity at \(x=3\text{.}\)