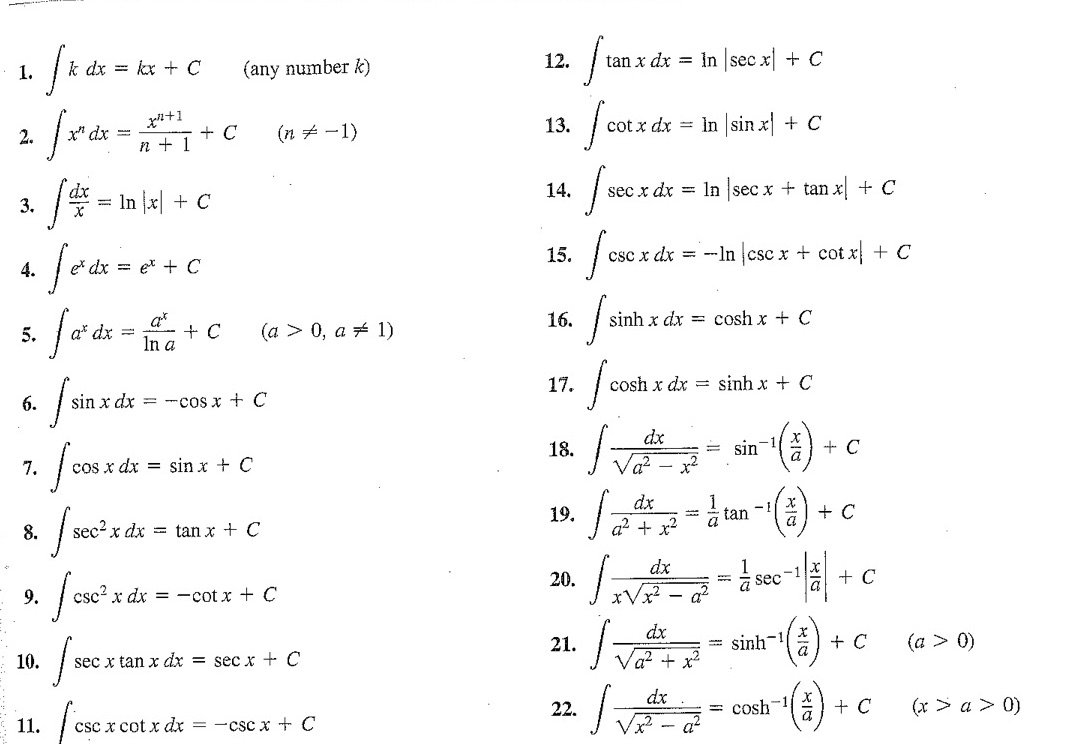Computing integrals

Unit 12 Computing integrals

All continuous functions have anti-derivatives, but not all of the anti-derivatives have names. For example, the definite integral \(\displaystyle\int_3^8 \frac{1}{\ln x} \, dx\) is a well defined quantity; indeed \(\displaystyle\int_a^b \frac{1}{\ln x} \, dx\) is well defined for any \(b > a > 1\text{,}\) but the function \(b \mapsto \displaystyle\int_a^b (1 / \ln x) \, dx\) is not equal to any combination of named functions such as powers, logs, exponentials and trig functions. The same is true of the normal (bell curve) density function \(e^{-x^2}\text{,}\) or \(\sqrt{\sin x}\) or \(\sqrt{1-4x^2} / \sqrt{1-x^2}\text{.}\) The prevalence of functions like this is the reason we need good numeric approximations to integrals. In the remainder of this section we concentrate on anti-derivatives for which reasonably nice exact expressions exist.

Subsection 12.1 Remembering and guessing

Computing derivatives, as you saw in Unit 6, rests on combination rules and working out some basic cases. For anti-derivatives the same is true, with" working out" replaced by "remembering". In other words, if you remember what the derivative of \(f\) is, then you know how to compute an anti-derivative of \(f'\text{.}\) This is how we computed anti-derivatives for polynomials, for example. The strategy is then: (1) list the derivatives we already know, organized in a way that allows us to query what function goes with a given derivative; and (2) give combining rules for anti-derivatives. This gives the following proposition. Note that in each case, remembering allows us to identify just one of the antiderivatives; we trust you can compute the others from that.

we use an integral sign without upper and lower limits to denote the antiderivative: e.g., \(\displaystyle\int (3x^2 + 1) \, dx\) is equal to \(x^3 + x\text{,}\) plus any constant. We usually write this as \(x^3 + x + C\text{.}\) By custom, we don't change the variable. In previous sections, for example, we were careful to write \(\displaystyle\int_0^b (3x^2 + 1) \, dx\) as a function of \(b\text{,}\) namely \(b^3 + b\text{.}\) But when writing the indefinite integral we tend to write \(\displaystyle\int (3x^2 + 1) \, dx = x^3 + x + C\text{,}\) not \(b^3 + b + C\text{.}\) This is because it's shorthand for

The indefinite integral of the function \(x \mapsto 3x^2 + 1\) is any function \(x \mapsto x^3 + x + C\text{.}\)

The variable \(x\) is bound, so the choice of letter does not affect the meaning.

Proposition 12.1.

The following basic anti-derivatives are computed by reversing Proposition 6.8.

\(\displaystyle\int x^m = \frac{1}{m} x^{m-1} + C\) as long as \(m \neq 0\text{.}\)
\(\displaystyle \displaystyle\int \frac{1}{x} \, dx = \ln x + C\)
\(\displaystyle \displaystyle\int \cos x \, dx = \sin x + C\)
\(\displaystyle \displaystyle\int \sin x \, dx = - \cos x + C\)
\(\displaystyle \displaystyle\int \sec^2 x = \tan x + C\)
\(\displaystyle \displaystyle\int e^x \, dx = e^x + C\)
\(\displaystyle \displaystyle\int \frac{1}{\sqrt{1-x^2}} \, dx = \arcsin x + C\)
\(\displaystyle \displaystyle\int \frac{1}{1+x^2} \, dx = \arctan x + C\)

Checkpoint 150.

Use Proposition 12.1 to compute this definite integral: \(\displaystyle\int_0^1 \frac{1}{1+x^2} \, dx\text{.}\) You will also need Proposition 11.24, which you should get used to using without even thinking of it as an extra step. Give an exact answer (not a decimal approximation).

Answer.

\(\frac{\pi }{4}\)

The derivative of a sum or difference is the sum or difference of the derivatives. The derivative of \(c \cdot f\) is \(c\) times the derivative of \(f\) for any real constant \(c\text{.}\) This leads immediately to the following proposition.

Proposition 12.2. linearity of the anti-derivative.

\begin{align*} \displaystyle\int [f(x) + g(x)] \, dx & =\displaystyle\int f(x) \, dx + \displaystyle\int g(x) \, dx \, ;\\ \displaystyle\int c \cdot f(x) \, dx & = c \cdot \displaystyle\int f(x) \, dx \, . \end{align*}

Proof of the first statement.

Let \(F\) be an anti-derivative of \(f\) and \(G\) be an anti-derivative of \(G\text{.}\) Thens \((F+G)' = F' + G' = f + g\) therefore \((F+G)\) is an antiderivative of \(f+g\text{.}\)

Checkpoint 151.

The proof of the second statement of Proposition 12.2 is even shorter. See if you can write it down.

The word "anti-derivative" is a mouthful and so is the verb form "anti-differntiate". Because computing integrals comes down to anti-differentiation, common practice is to use the verb integrate in place of "anti-differentiate". We also call an anti-derivative an "integral". Proposition 12.1 and Proposition 12.2 allow us to compute some more integrals.

Example 12.3.

Let's compute the integral of \(\frac{a \cos x + b / \cos x}{\cos x}\text{.}\) Simplifying,

\begin{equation*} \frac{a \cos x + b / \cos x}{\cos x} = a + b \sec^2 x \, . \end{equation*}

Therefore

\begin{align*} \displaystyle\int \frac{a \cos x + b / \cos x}{\cos x} \, & dx \\ & = \displaystyle\int [a + b \sec^2 x] \, dx \\ & = \displaystyle\int a \, dx + b \displaystyle\int \sec^2 (x) \, dx \\ & = ax + \tan x + C \, \end{align*}

Checkpoint 152.

One of your classmates argues that Example 12.3 is wrong: \(\displaystyle\int a \, dx = ax + C\) and \(\displaystyle\int \sec^2 (x) \, dx = \tan x + C\text{,}\) therefore the answer should be \(ax + \tan x + 2C\text{.}\) What is going on?

The text's answer is correct.
Your classmate's answer is correct.
Both answers are correct.

Answer.

\(\text{Choice 3}\)

Example 12.3 should worry you. Does it seem a bit contrived? The expression \(\frac{a \cos x + b / \cos x}{\cos x}\) just happens to simplify into two expressions covered by the list of cases in Proposition 12.1. If that seems like a piece of luck, it is. With only Proposition 12.1 and Proposition 12.2 you won't get very far. The next two sections give two rules for combining integrands that will greatly increase your ability to integrate. Keep in mind though, that in some sense you are still lucky whenever you can compute an analytic expression for an anti-derivative: many anti-derivatives have no nice formula.

Subsection 12.2 Integration by parts

The sum rule for derivatives is simple enough that it leads directly to the first statement of Proposition 12.2, which is an identical rule for anti-derivatives. There is also a product rule, but it does not lead directly to an identical rule for anti-derivatives. That's because the product rule for derivatives is not symmetric. The derivative of \(fg\) is not \(f' g'\) but rather \(f'g + g'f\text{.}\) When we run the product rule backwards, we get

\begin{equation} \displaystyle\int \left[f'(x) g(x) + g' (x) f(x)\right] \, dx = f(x) g(x) + C \, .\label{eq-anti-product}\tag{12.1} \end{equation}

The problem is, this doesn't tell us how to integrate a product such as \(f' g'\text{!}\) (12.1) is great if someone asks us to compute the anti-derivative of \(f'g + g'f\text{,}\) but this is rare, harder to spot, and does not answer the question as to the anti-derivative of a product.

The best we can do is to exploit (12.1) as much as we can. This leads to the following proposition.

Proposition 12.4. integration by parts.

Let \(u\) and \(v\) be differentiable functions. Suppose \(u' v\) is known to have anti-derivative \(G\text{.}\) Then \(v' u\) has anti-derivative \(u v - G\text{.}\) In a single equation,

\begin{equation} \displaystyle\int v' u \, dx = uv - \displaystyle\int u' v \, dx \, .\label{eq-parts}\tag{12.2} \end{equation}

Proof.

This is just the product rule for derivatives run in reverse: \((uv) ' = u'v + v'u\text{,}\) therefore

\begin{equation*} (uv - G)' = u'v + v'u - G' = v' u \, . \end{equation*}

The way this works in practice is that when integrating an expression, you try to identify the expression as \(v' u\) for some functions \(u\) and \(v\text{.}\) Then you check whether you already know the anti-derivative to \(u' v\text{.}\) If so, you subtract this from \(uv\) and you are done. Sometimes there are several possible ways to do this, in which case you may have to try them all until you find one that works.

Example 12.5.

Use integration by parts to integrate \(x e^x\text{.}\) Oviously this decomposes as a product of \(x\) and \(e^x\text{.}\) One of these should be \(v'\) and the other should be \(u\text{.}\) Let's try setting

\begin{align*} v' & = x \, ;\\ u & = e^x \, \end{align*}

At first this goes smoothly: the expression we chose for \(v\) has a known anti-derivative and the one we chose for \(u\) has a known derivative, therefore we can find \(v\) and \(u'\text{:}\)

\begin{align*} v & = \frac{x^2}{2} + C \, ;\\ u' & = e^x \, \end{align*}

Unfortunately the next step doesn't work: \(u' v = e^x (x^2/2 + C)\text{,}\) which is not something whose anti-derivative we recognize no matter what choice we make for the constant \(C\text{.}\)

Back to the drawing board. Let's try the other possible assignment of roles:

\begin{align*} v' & = e^x \, ;\\ u & = x \, \end{align*}

Again it goes smoothly at first: the expression we chose for \(v\) has a known integral \(e^x\) and the one we chose for \(u\) has a known derivative \(1\text{,}\) therefore

\begin{align*} v & = e^x + C \, ;\\ u' & = 1 \, \end{align*}

Now we're in better shape. Choose \(C=0\) (usually this works if anything does). Then \(u'v = e^x\text{,}\) for which an integral is known, namely \(e^x\text{.}\) Therefore,

\begin{equation*} \displaystyle\int x e^x \, dx = \displaystyle\int u v' \, dx = uv - \displaystyle\int u' v \, dx = x e^x - \displaystyle\int e^x \, dx = x e^x - e^x + C \, . \end{equation*}

We did a long-winded example to show you the process of trial and error and to show how each step works. What would have happened if we chose a different value of \(C\text{?}\) It turns out it always works exactly as well.

Checkpoint 153.

Complete the computation in the previous example, choosing \(C=7\) instead of \(C=0\text{.}\) What happens?

It usually takes several worked examples and a lot of practice before integration by parts feels natural. Because "a lot of practice" means different things to different people, we include only a few mandatory self-check and howework problems, putting a greater number online for those who want to practice.

Example 12.6.

Compute the definite integral \(\displaystyle\int_0^{2\pi} x \sin (x) \, dx\text{.}\) We start with the indefinite integral, which we compute by parts. Based on what happened with \(x e^x\text{,}\) let's decide to start with the choice \(u = x, v' = \sin x\text{.}\) Then \(v = - \cos x\) and \(u' = 1\text{,}\) which yields

\begin{equation*} \displaystyle\int x \sin(x) \, dx = - x \cos x - \displaystyle\int (- \cos x) \, dx = - x \cos x - (- \sin x) = \sin x - x \cos x + C \, . \end{equation*}

Evaluating the definite integral (notice we chose \(C=0\)),

\begin{align*} \displaystyle\int_0^{2\pi} x \sin (x) \, dx & = \left [ \sin x - x \cos (x) \right ]_{x=2\pi} - \left [ \sin x - x \cos (x) \right ]_{x=0} \\ & = [\sin (2\pi) - 2 \pi \cos(2 \pi)] - [\sin(0) - 0 \cdot \cos(0)] \\ & = - 2 \pi \, \end{align*}

Checkpoint 154.

Evaluate \(\displaystyle\int_0^\pi x \cos (x) \, dx\text{.}\)

Answer.

\(-2\)

Here are a few more tips to help you use integration by parts. Also, you should see a notational variation that is common in textbooks and on the web. Instead of \(\displaystyle\int v' u \, dx = uv - \displaystyle\int u' v \, dx\text{,}\) people sometimes write

\begin{equation*} \displaystyle\int u \, dv = uv - \displaystyle\int v \, du \, . \end{equation*}

Because \(u\) and \(v\) are functions of \(x\text{,}\) you can think of \(du := u'(x) \, dx\) and \(dv := v' (x) \, dx\text{,}\) whereby this form of the identity comes out to exactly the same thing as (12.2)

Repeated integration by parts.

Sometimes integration by parts doesn't quite get you to an expression \(u'v\) that you know how to evaluate, but it gets you closer, so that repeating the integration by parts solves the problem.

Example 12.7.

We'll compute \(\displaystyle\int x^2 e^x\text{.}\) Letting \(v' = e^x\) and \(u = x^2\) gives

\begin{equation*} \displaystyle\int x^2 e^x \, dx = x^2 e^x - \displaystyle\int 2 x e^x \, dx \, . \end{equation*}

That last expression isn't covered by Proposition 12.1 but we just saw (take out the constant factor 2) that it can be done by parts and integrates to \(2 (x e^x - e^x) = 2 (x-1) e^x\text{.}\) Therefore,

\begin{equation*} \displaystyle\int x^2 e^x \, dx = x^2 e^x - 2 (x-1) e^x = (x^2 - 2x + 2) e^x \, . \end{equation*}

It should be apparent you can integrate \(p(x) e^x\) this way for any polynomial \(p\text{.}\) Some textbooks have a separate algorithm for this called tabular integration. We won't be teaching that, but you can google it if you ever need the anti-derivative of \(p(x) e^x\) where \(p(x)\) has degree more than, say, 3 (doing it by hand gets longer and more complicated as the degree of \(p\) grows). To see how this will go, try the following exercise, which is about as much as we would ever ask you to do by hand.

Checkpoint 155.

Compute \(\displaystyle\int x^3 e^x\text{.}\)

Double check afterward by differentiating your answer.

Answer.

\(e^{x}\!\left(x^{3}-3x^{2}+6x-6\right)+C\)

Don't forget \(v'\) could be 1.

You can always decompose any expression as itself times 1. In the langauge of \(v \, du\) and \(u \, dv\text{,}\) that says \(\displaystyle\int f (x) \, dx\) can always be thought of as \(u \, dv\) where \(u(x) = f(x)\) and \(dv = dx\text{,}\) that is, \(v' = 1\text{.}\) This only sometimes works but it's good to know.

Example 12.8.

Compute \(\displaystyle\int \ln (x) \, dx\text{.}\) There's only one term to decompose so we pretty much have to use the \(dv = dx\) trick. Setting \(u(x) = \ln x\) and \(dv = dx\text{,}\) gives (recalling that the derivatve of \(\ln x\) is \(1/x\)),

\begin{equation*} \displaystyle\int \ln (x) \, dx = (\ln x) (x) - \displaystyle\int x \cdot \frac{1}{x} \, dx = x \ln x - \displaystyle\int 1 \cdot dx = x \ln x - x + C \, . \end{equation*}

This is a good one to memorize - it's very useful to recall quickly how to integrate the natural log.

Subsection 12.3 Substitution

Integration by parts is what you get from reversing the product rule. Reversing the chain rule is called substitution. You can probably guess what it says. The chain rule says \((d/dx) f(g(x)) = f'(g(x)) g'(x)\text{.}\) Therefore, we need a rule to tell us that \(\displaystyle\int f'(g(x)) g'(x) \, dx = f(g(x))\text{.}\) This gives the simplest form of the substitution method.

Theorem 12.9.

Suppose \(g\) is differentiable on an interval \((a,b)\) and let \(I\) (which will also be a closed interval) be the range of \(g\text{.}\) Suppose \(h\) is differentiable on \(I\text{.}\) Then

\begin{equation*} \displaystyle\int h'(g(x)) g'(x) \, dx = h(g(x)) + C \, . \end{equation*}

Writing \(f\) for \(h'\text{,}\) this becomes

\begin{equation} \displaystyle\int f(g(x)) g'(x) \, dx = \left ( \displaystyle\int f \right ) \circ g\label{eq-subs}\tag{12.3} \end{equation}

where the identity \(f = h'\) allows us to write the indefinite integral \(\displaystyle\int f\) in place of \(h\) on the right. This second form is sometimes clearer because we often arrive at the form \(f(g(x)) g'(x)\) before we have identified the antiderivative of \(f\text{,}\) hence it makes sense for the right-hand side to leave \(\displaystyle\int f\) unevaluated.

Example 12.10.

We compute the integral of \(\frac{(\ln x)^2}{x}\text{.}\) The numerator \((\ln x)^2\) looks like a composition \(f(g(x))\) where \(f(x) = x^2\) and \(g(x) = \ln x\text{.}\) We are in luck because \(g'(x) = 1/x\) so there is alread a \(g'\) sitting there. The expression to be integrated looks like \(f(g(x)) g'(x)\text{,}\) so applying (12.3),

\begin{equation*} \displaystyle\int \frac{(\ln x)^2}{x} \, dx = \left ( \displaystyle\int x^2 \right ) \circ \ln \, . \end{equation*}

The indefinite integral of \(x^2\) is \(x^3 / 3\text{,}\) so the final answer is that the indefinite integral of \((\ln x)^2 / x\) is \((\ln x)^3 / 3 + C\text{.}\)

Checkpoint 156.

Use the substitution method to evaluate \(\displaystyle\int (2x) e^{x^2} \, dx\text{.}\)

Answer.

\(e^{x^{2}}+C\)

The substitution rule is very often stated in the language of science, with a variable \(u\text{,}\) thought of as a physical quantity related to the variable \(x\) via \(u = g(x)\text{.}\)

Instead of a theorem, this version is usually described as a procedure.

Change variables from \(x\) to \(u\) (hence the common name "\(u\)-substitution")
Keep track of the relation between \(dx\) and \(du\)
If you chose correctly you can now do the \(u\)-integral
When you're done, substitute back for \(x\)

Again, we let \(g\) be the function relating \(u\) to \(x\) via \(u = g(x)\text{,}\) and again you need hypotheses, namely the ones stated in Theorem 12.9). Then \(du = g'(x) \, dx\text{.}\) Usually you don't do this kind of substitution unless there will be an \(g' (x) \, dx\) term waiting which you can then turn into \(du\text{.}\) Also, you don't do this unless the rest of the occurences of \(x\) can also be turned into \(u\text{.}\) If \(g\) has an inverse function, you can do this by substituting \(g^{-1} (u)\) for \(x\) everywhere. Now when you reach the fourth step, it's easier because you can just plug in \(u = g(x)\) to get things back in terms of \(x\text{.}\)

This notation gives a particularly nice simplification when \(u = x + c\) for some constant \(c\text{.}\) Replacing \(x\) by \(x+c\) is called a translation. In the first unit of the course, we discussed what this does to the graph. It is a very natural change of variables, corresponding to a different starting point for a parametrization.

Example 12.11. translation.

Compute the indefinite integral of \(\sqrt{x+6}\text{.}\) Let \(u = x+6\text{.}\) Then \(du = dx\text{.}\) Integrating the \(1/2\) power (one of the basic facts in Proposition 12.1),

\begin{equation*} \displaystyle\int \sqrt{x+6} \, dx = \displaystyle\int \sqrt{u} \, du = \frac{2}{3} u^{3/2} = \frac{2}{3} (x+1)^{3/2} + C \, . \end{equation*}

The moral of this story is that you can "read off" integrals of translations. For example, knowing \(\displaystyle\int \cos x \, dx = \sin x+C\) allows you to read off \(\displaystyle\int \cos (x-\pi/4) \, dx = \sin (x - \pi/4)+C\text{.}\) Don't let this example fool you into thinking it works this way for functions other than translations. Thinking that \(\displaystyle\int \cos (\sqrt{x}) \, dx = \sin (\sqrt{x}) + C\) is wrong; it is the calculus equivalent of the algebra mistake \((a+b)^2 = a^2 + b^2\text{.}\)

Here's an example of \(u\)-substitution with something other than a translation.

Example 12.12.

Let's compute \(\displaystyle\int \sin^n x \, \cos x \, dx\text{.}\)

Solution: substitute \(u = \sin x\) and \(du = \cos x \, dx\text{.}\) This turns the integral into \(\displaystyle\int u^n \, du\) which is easily valuated as \(u^{n+1} / (n+1) + C\text{.}\) Now plug back in \(u = \sin x\) and you get the answer

\begin{equation*} \frac{\sin^{n+1} x}{n+1} + C \, . \end{equation*}

You might think to worry whether the substitution had the right domain and range, was one to one, etc., but you don't need to. When computing an indefinite integral you are computing an anti-derivative and the proof of correctness is whether the derivative is what you started with. You can easily check that the derivative of \(\sin^{n+1} x / (n+1)\) is \(\sin^n x \cos x\text{.}\)

After a translation, the next simplest substitution is a dilation, where \(u(x) = c x\) for some nonzero real number \(c\text{.}\) This is the other case in which substitution always succeeds: if you can integrate \(f(x)\) you can always integrate \(f(cx)\text{.}\) We leave it to you to work this out, first in an example, then in the general case.

Checkpoint 157.

Use substitution to integrate \(\cos (5x)\text{.}\)

Suppose you know the anti-derivative for \(f\text{;}\) say \(f = h'\text{.}\) Use subsitution to work out the general formula for \(\displaystyle\int f(cx) \, dx\text{.}\)

Answer. 1

\(\frac{1}{5}\sin\!\left(5x\right)+C\)

Answer. 2

\(\frac{1}{c}hcx+C\)

When evaluating a definite integral you can compute the indefinite integral as above and then evaluate. A second option is to change variables, including the limits of integration, and then never change back.

Example 12.13.

Let's compute \(\displaystyle\int_1^2 \frac{x}{x^2+1} \, dx\text{.}\)

If we let \(u = x^2+1\) then \(du = 2x \, dx\text{,}\) so the integrand becomes \((1/2) \, du / u\text{.}\) If \(x\) goes from 1 to 2 then \(u\) goes from 2 to 5, thus the integral becomes

\begin{equation*} \displaystyle\int_2^5 \frac{1}{2} \frac{du}{u} = \frac{1}{2} (\ln 5 - \ln 2) \, . \end{equation*}

Of course you can get the same answer in the usual way: the indefinite integral is \((1/2) \ln u\text{;}\) we substitute back and get \((1/2) \ln (x^2 + 1)\text{.}\) Now we evaluate at 2 and 1 instead of 5 and 2, but the result is the same: \((1/2) (\ln 5 - \ln 2).\)

Backwards substitution.

There are times when the best substitution is of the form \(x = g(u)\) rather than \(u = g(x)\text{.}\) No matter what \(f\) and \(g\) are, the substitution \(x = g(u), \; dx = g'(u) \, du\) always leads to a new integral, it's just hard to choose \(g\) in a way that makes the new integral simpler than the old one. It turns out there are some integrals, not apparently involving trig functions, where substituting \(x = g(u)\) for some trig function \(g\) will magically unlock a dead end. Knowing tricks for dealing with a wide class of anti-derivative extractions is not the aim of this course, therefore we will not be featuring this method in the text. If you're interested in seeing one of these, try googling "integrate sqrt(1-x^2)".

Looking it up.

Math is about understanding relations of a precise nature, about abstraction, and about making models of physical phenomena. It is also about building a library of computational tricks, but that's only a small part of math, and it's somewhat time-consuming. We have taught you what we think it is reasonable for you to know and remember -- to have in your quick-access library. For all the other integrals currently known to mankind, there are lookup tables. The following integral table is stolen from a popular calculus book. Use it as a reference as needed.