Unit 8 Optimization
In this section, we'll apply the tool of differentiation to a broad sort of problem called optimization. The idea is, given a mathematical model, to come up with the largest, smallest, cheapest, most profitable, lowest-risk, fastest, safest, or whatever -est word applies to the situation.
Many of you have seen max-min problems before. If not, pay attention! Finding the maximum or minimum of a function is one of the crowning achievements of calculus, with applications in literally any field where mathematical modeling is done.
Subsection 8.1 Definitions of Minima and Maxima, and their existence
The following definitions give precise meaning to notions you have probably already seen. Some vocabulary may be new but none of it is rocket science.
Definition 8.1.
- minimum
- A point \(x \in [a,b]\) such that \(f(x) \leq f(y)\) for all \(y \in [a,b]\) is where \(f\) achieves its minimum (plural: minima). The value \(f(x)\) is the minimum. This is also called a global or absolute minimum on \([a,b]\text{.}\)
- maximum
- A point \(x \in [a,b]\) such that \(f(x) \geq f(y)\) for all \(y \in [a,b]\) is where \(f\) achieves its maximum (plural: maxima). This is also called a global or absolute maximum on \([a,b]\text{.}\) The value \(f(x)\) is the maximum.
- extremum
- The word for a something that is a minimum or maximum is extremum (plural: extrema) or extreme value.
- local minimum
- A value \(x\) such that \(f(x) \leq f(y)\) for all \(y\) in some open interval \(I\) containing \(x\text{,}\) which could be a lot smaller than the whole interval \((a,b)\text{,}\) is where \(f\) achieves its local minimum. The terms local maximum and local extremum are defined analogously.
- critical point
- a point where \(f'\) is zero or undefined.
Note 8.2.
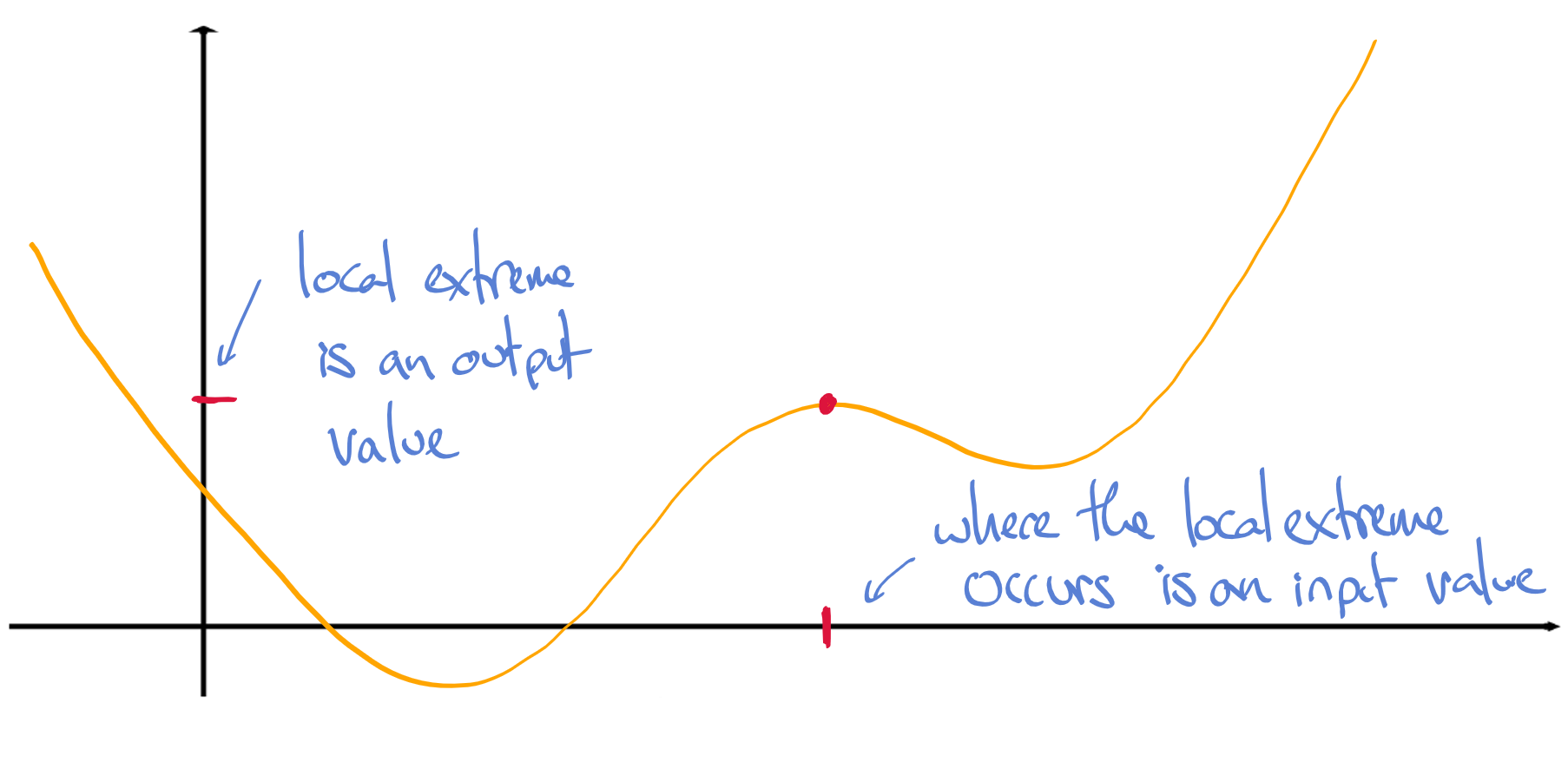
A somewhat subtle but important note about the language here: the input value \(x\) is where the extremum is achieved; the extremum itself is always an output value.
In applications, we sometimes want to know just what the maximum is (an output); sometimes just where the maximum occurs (an input); and sometimes both. By way of example:
- If I want to build a building to house my flying squirrels, I need to know what the maximum height they're capable of flying is, but I don't really care when they get to that height.
- If I need to build a window which admits the most possible light, what I care about is how to set the dimensions (an input), but the amount of light actually let in (in lumens, say) isn't really needed.
- If I'm running a widget factory and I want to know what production level will maximize my profit, the input where the maximum occurs (a number of widgets per hour) is important, but for fiscal planning I also need to know what that maximum (a number of dollars) actually is.
As you may have noticed, we'll reserve the word what to refer to the extremum itself (the output value), and talk about when, where, or how that extremum occurs.
Before we start looking for extrema, it might occur to you to question whether they exist. Better not to go on a wild goose chase.
Checkpoint 100.
- Find a discontinuous function defined on the interval \([-2 , 1]\) with no absolute maximum nor minimum on that interval.
- Find a continuous function on \((-2 , 1)\) with no absolute maximum nor minimum on that interval.
Now that you have seen some scenarios where functions have no absolute extrema on an interval, here is a theorem guaranteeing the opposite.
Theorem 8.4.
Let \(f\) be a continuous function on the closed interval \([a,b]\text{.}\) Then \(f\) has at least one absolute minimum on \([a,b]\) and at least one absolute maximum on \([a,b]\text{.}\)
Checkpoint 101.
What assumption of Theorem 8.4 is violated in each part of your answer to Checkpoint 8.1?
Subsection 8.2 The first derivative and extrema
Theorem 8.5. Fermat's Theorem.
Suppose a function \(f\) has a minimum at a point \(c\) in some open interval \(I\text{.}\) If \(f\) is differentiable at \(c\) then \(f'(c) = 0\text{.}\)
The proof of this theorem is accessible and conceptually relevant. This result should seem very credible an intuitive level. If \(f'(c) > 0\) then moving to the left from \(c\) to \(c - \varepsilon\) should produce a greater value of \(f\text{.}\) Likewise, if \(f' (c) < 0\) then moving to the right should produce a greater value. This is the most intuitive justification we could write down, though not exactly airtight.
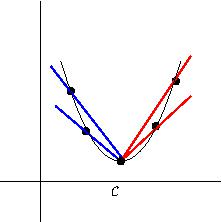
Here is a more airtight argument. Because \(f\) is differentiable at \(c\text{,}\) the one-sided derivatives exist and are equal. The derivative from the right is \(\lim_{x \to c^+} \frac{f(x) - f(c)}{x-c}\text{;}\) because \(c\) is a minimum, both top and bottom of this fraction are positive (the numerator could be zero). The limit of nonnegative numbers is nonnegative, hence \(f'(c_+) \geq 0\text{;}\) see Figure 8.6. Similarly, \(f'(c_-)\) is a limit in which each term is nonpositive, thus \(f' (c_-) \leq 0\text{.}\) For these to be equal, both must equal zero. This finishes the proof.
Checkpoint 102.
Suppose \(f\) is differentiable on \([a,b]\) (derivatives at the endpoints are one-sided). If the minimum of \(f\) on this interval occurs at the left endpoint, can you conclude that the one-sided derivative there is zero?
yes, we can conclude that
no, we cannot conclude that
Explain.
\(\text{no, we cannot conclude that}\)
Let's get the logic straight. It is of the form {\tt minimum \(\Rightarrow\) \(f' = 0\)}. The converse is not necessarily true: {\tt \(f' = 0\) \(\Rightarrow\) minimum}. Nevertheless, everyone's favorite procedure for finding minima is to set \(f'\) equal to zero. Why does this work, or rather, when does this work?
Let \(a < b\) be real numbers. First of all, does \(f\) even have a minimum on \([a,b]\text{?}\) In fact there are counterexamples in Figure 8.7.
From Theorem 8.4, if \(f\) is defined and continuous on a closed interval \([a,b]\text{,}\) then indeed \(f\) has to have a minimum somewhere on \([a,b]\text{.}\) We can find it by using Theorem 8.5 to rule out where it's not: if \(a < c < b\) and \(f'(c) \neq 0\text{,}\) then definitely the minimum does not occur at \(c\text{.}\) Where can it be then? What's left is the point \(a\text{,}\) the point \(b\text{,}\) every point where \(f'\) is zero, and every point where \(f'\) does not exist. An identical argument shows the same is true for the maximum. Summing up:
Theorem 8.8.
Suppose \(f\) is continuous on \([a,b]\) and differentiable everywhere on \((a,b)\) except for a finite number of points \(c_1, \ldots, c_k\text{.}\) Then the minimum value of \(f\) on \([a,b]\) occurs at one or more of the points \(\{ a, b, c_1, \ldots , c_k , \mbox{ anywhere } f' = 0 \}\text{,}\) and nowhere else. The maximum also occurs at one or more of these points and nowhere else.
Checkpoint 103.
Let \(f(x) := \lvert x\rvert\) and let \([a,b]\) be the interval \([-2,2]\text{.}\) Does the theorem say \(f\) must have a minimum on this interval?
Yes, f must have a minimum.
No, the Theorem is silent about this.
No, the Theorem says f does not have a minimum.
If so, what does the theorem say about where the minimum must be?
Now answer the same question for the maximum of \(f\) on a general interval \([a,b]\text{.}\)
Remark 8.9.
Being differentiable except for a number of points (call them \(c_0,\ldots,c_k\)) is sometimes called being piecewise differentiable, because the function is differentiable in pieces, the pieces being the intervals \((c_0, c_1) , (c_2, c_2), \ldots , (c_{k-1} , c_k)\text{.}\)
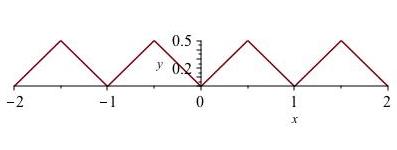
Checkpoint 104.
Let \(f\) be the “sawtooth” function shown in Figure 8.10, defined by letting \(f(x)\) be the distance from \(x\) to the nearest integer, either \(\lfloor x \rfloor\) or \(\lceil x \rceil\text{.}\)
Is \(f\) piecewise differentiable on \([-2,2]\text{?}\)
yes
no
\(\text{no}\)
You can write Theorem 8.8 as a procedure if you want. Even if you're looking only for the minimum or only for the maximum, the procedure is the same so it will find both.
- Make sure \(f\) is continuous on \([a,b]\text{;}\) if not, abort procedure.
- Write down all \(x \in (a,b)\) where \(f'(x) = 0\text{.}\)
- Add to the list all \(x \in [a,b]\) where \(f'(x)\) DNE.
- Add to the list the points \(a\) and \(b\text{.}\)
- For every point \(x\) on the list, compute \(f(x)\text{;}\) the greatest value on this second list (the output list) will be the maximum; the least will be the minimum.
- Using the two lists side by side, we can determine where the extrema occurred.
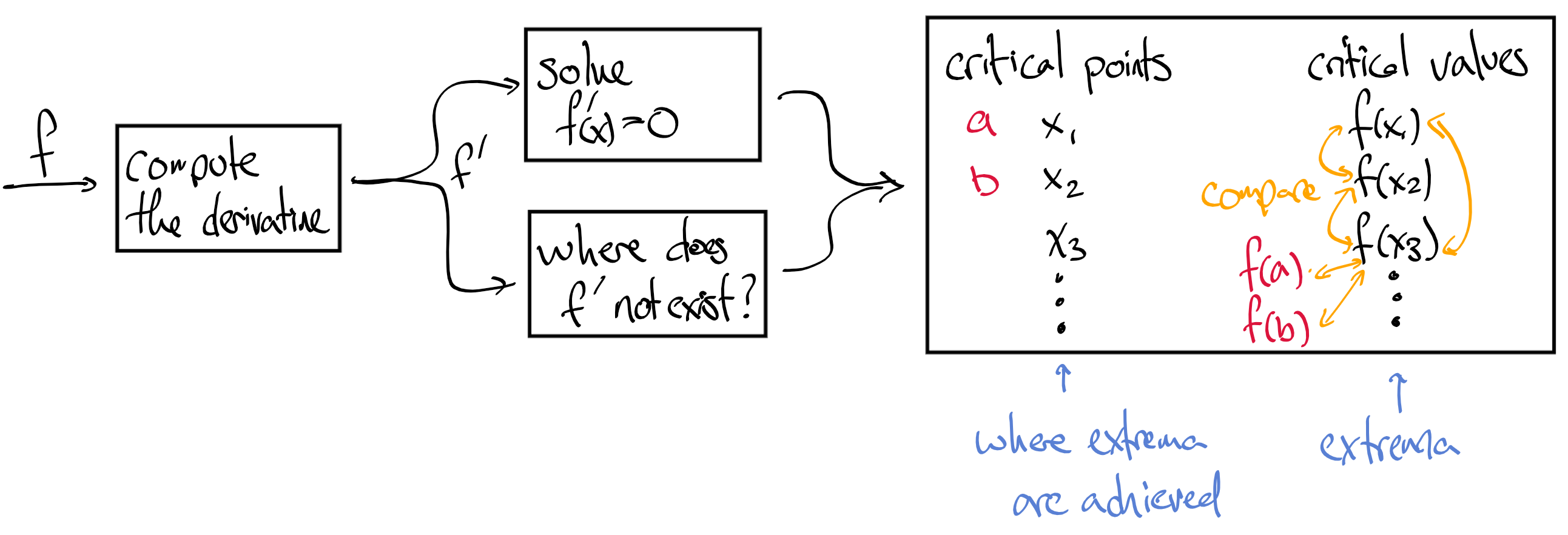
Example 8.12.
Find the maximum of \(f(x) := 5x - x^2\) on the interval \([1,3]\text{;}\) see the figure at the right. Computing \(f'(x) = 5-2x\) and setting it equal to zero we see that \(f'(x) = 0\) precisely when \(x = 2 \frac{1}{2}\text{.}\) There are no points where \(f\) is undefined, so our list consists of just the one point plus the two endpoints: \(\{ 1, 2 \frac{1}{2}, 3 \}\text{.}\) Checking the values of \(f\) there produces \(4, 6 \frac{1}{4}, 6\text{.}\) The maximum is the greatest of these, occurring at \(x = 2 \frac{1}{2}\text{.}\)
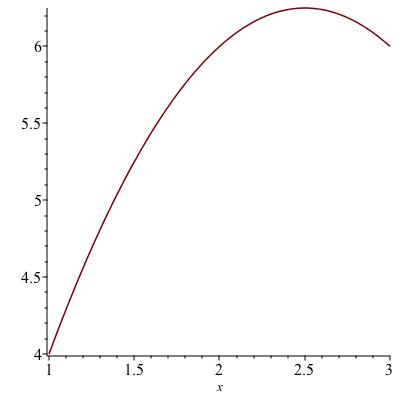
Checkpoint 105.
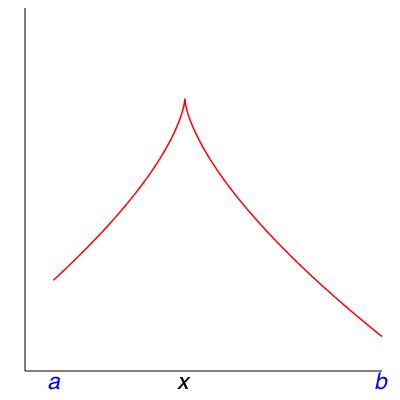
1.
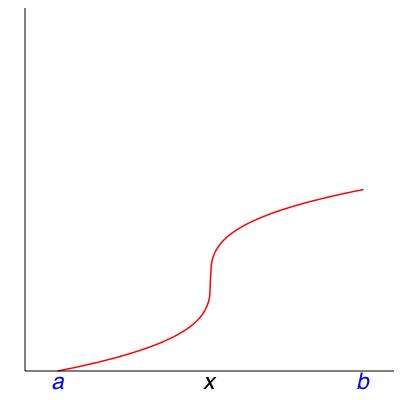
2.
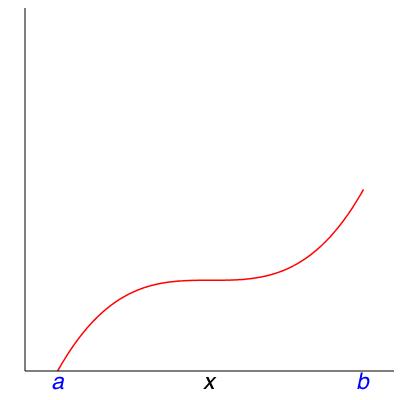
3.
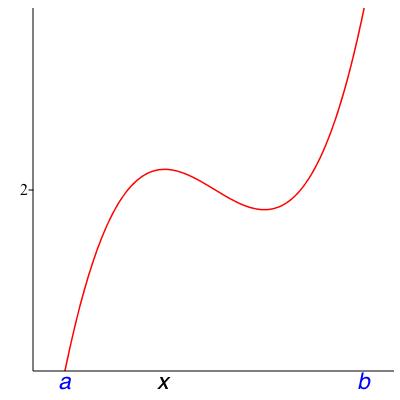
4.
Checkpoint 106.
Here are some other things you may find when you use Theorem 8.8. Match each of these verbal descriptions to the role of \(x\) in one of the four pictures in Figure 8.14.
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
Which picture has an endpoint that is not where the function achieves a global extremum?
Example 8.15. If the interval is not closed, the function might have no minimum.
Let \(f(x) = x\) and consider the half-closed interval \((0,1]\text{.}\) In this case we have a continuous function but not a closed interval.
This example represents a scenario where you make a donation in bitcoin to enter a virtual tourist attraction and you want to spend as little as possible. You have 1 bitcoin, so that's the maximum you can donate; donations can be any positive real number but zero is not allowed.
The minimum of \(x\) on \((0,1]\) does not exist: there is no smallest positive real number.
The interpretation is clear: no matter how little you donate, you could have donated less. Mathematically, this clarifies the need for a closed interval in Theorem 8.4.
Checkpoint 107.
Second derivatives and extrema.
Recall that wherever \(f\) has a second derivative, if \(f'' \neq 0\) then the sign of \(f''\) determines the concavity of \(f\text{.}\) If \(f''(x) > 0\) then \(f\) is concave upward and if \(f''(x) < 0\) then \(f\) is concave downward. At a point where \(f' = 0\text{,}\) if we know the concavity, we know whether \(f\) has a local maximum or local minimum.


Example 8.17.
What are the extrema of the function \(f(x) := x^2 + 1/x\) on the interval \((0,2)\text{?}\) The only critical point is where \(f'(x) = 2x - 1/x^2 = 0\text{,}\) hence \(x = \sqrt[3]{1/2}\text{.}\) Here, \(f''(x) = 2 + 2/x^3 > 0\) therefore this is a local minimum. There are not any local maxima. This means \(f\) has no global maximum on \((0,2)\text{.}\) It may have a global minimum, and indeed, Figure 8.18 shows that \(x = \sqrt[3]{2}\) is a local minimum. In your homework you will get some more tools for arguing whether a local extremum on a non-closed interval is a global extremum.
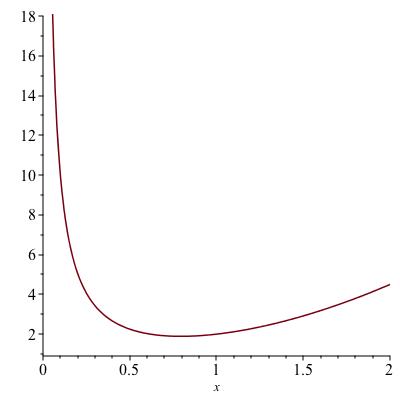
Remark 8.19.
If the second derivative vanishes along with the first, you won't know any more than you did already.
Subsection 8.3 Some example applications
Finding extrema is part of a subject called optimization. The idea is that you control a parameter \(x\) and are would like to maximize some objective function \(f(x)\text{,}\) which is perhaps how large you can build something, or perhaps revenue minus cost, or the efficiency of extraction of a natural resource.
Example 8.20.
The logistic equation models growth rate per unit time, call it \(R\text{,}\) of a population as \(R(x) = C x (A-x)\text{.}\) Here \(C\) is a constant of proportionality, \(x\) is the present population, and \(A\) is a theoretical limit on the population size supported by the habitat. At what size is the population growing the fastest?
We need to find the maximum of \(R(x) := C x (A-x)\) on \([0,A]\text{.}\) The reason for restricting to this interval is that we are told the population size is constrained to be at most \(A\text{,}\) and of course it has to be nonnegative. Computing \(R'(x) = C (A - 2x)\text{,}\) we find \(R' = 0\) for a single value, \(x = A/2\text{.}\) Checking the endpoints, we find \(R\) is zero at both. Therefore the maximum value occurs at \(x = A/2\text{.}\)
Checkpoint 108.
Example 8.21.
Suppose the cost of supplying a station is proportional to the distance from the station to the nearest port, and the cost of the land for the station is inversely proportional to the distance to the nearest port. Adding together these costs, what is the least expensive distance at which to put the station?
Letting \(x\) be the distance to the nearest port and \(f(x)\) be the cost, we are told that \(f(x) = a x + b/x\) where \(a\) and \(b\) are unspecified constants. The value of \(f(x)\) is defined for every positive \(x\) and \(f\) is continuous on \((0,\infty)\text{.}\) We seek the global minimum of \(f\) on \((0,\infty)\text{.}\) We are not guaranteed there is a minimum. When we solve for \(f'(x) = 0\) we find
At this value, \(f(x) = a \sqrt{\frac{b}{a}} + b/\sqrt{\frac{b}{a}} = 2 \sqrt{ab}\text{.}\) Checking what happens near~0 and \(\infty\text{,}\) we find \(\lim_{x \to 0} f(x) = \infty\) and \(\lim_{x \to \infty} f(x) = \infty\text{.}\) Therefore, there is a minimum value, which we have determined to be \(\sqrt{ab}\) occuring at \(x = \sqrt{\frac{a}{b}}\text{.}\)
Example 8.22.
The functions \(x^\gamma e^{-x}\text{,}\) for \(x \geq 0\text{,}\) arise in probability modeling. They are called Gamma densities. We will return to these in Unit 14. For now, we would like to understand the shape of these functions. An example with \(m=5\) is shown in Figure 8.23.
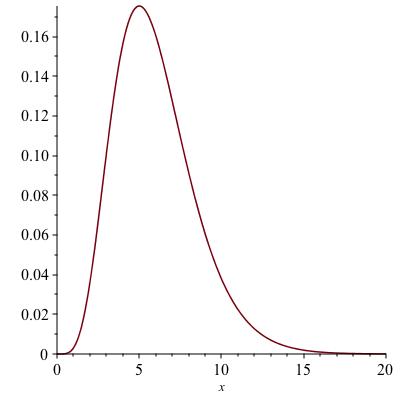
The place where one is mostly to find the random variable is where the maximum of the density occurs. Where does the maximum of \(f(x) := x^5 e^{-x}\) occur? We know that the value is zero at \(x=0\) and positive everywhere else. We also know \(\lim_{x \to \infty} f(x) = 0\text{.}\) This means there must be a maximum at some positive finite \(x\text{.}\) The function \(f\) is differentiable for all positive \(x\text{,}\) therefore the maximum can only occur where \(f' = 0\text{.}\) Solving
Factoring out \(x^4 e^{-x}\text{,}\) we see that \(x=5\text{.}\) Therefore, the maximum occurs at \(x=5\text{.}\)
Checkpoint 109.
Why does a limit of zero at infinity imply that \(f\) must have a maximum at some positive, finite \(x\text{?}\)
Example 8.24.
Let \(h\) be the height of a member of a carnivore species. In this simple model, the food gathering capability of an individual is given by \(k h^2\) while its daily food needs are given by \(c h^3\text{.}\)
- Why?
- We can only make educated guesses about the reason the equations in the model have this form. If an animal's speed is proportional to its height then the model stipulates territory is proportional to the square of this. Perhaps territory is the area that can be reached in a given amount of time such as an hour or a day. As to why food needs would be proportional to volume, one might imagine that sustaining and nourishing tissue requires nutrients proportional to volume.
- What are the units of \(c\) and \(k\text{?}\)
- Units of \(c\) are food per length\(^3\) and units of \(k\) are food per length\(^2\text{.}\) For example, if food is measured in kilograms and length in meters, then food per length\(^3\) would be kg/m\(^3\text{;}\) however one might measure food in other ways such as calories, or numbers of a particular animal of prey, etc.
- To maximize food gathering ability minus food needs, how tall should members of this species be?
- The objective function we want to maximize is \(k h^2 - c h^3\text{.}\) Having been told no limitations on size, we assume \(h\) can be any positive real number, though we may have to retract that if the optimum turns out to have unrealistic scale. Differentiating \(f(h) := k h^2 - c h^3\) with respect to \(h\) yields \(2 k h - 3 c h^2\) and setting equal to zero gives the two solutions \(0\) and \(x_* := (2k) / (3c)\text{.}\) This indeed has units of length. Clearly \(f(0) = 0\text{.}\) The value of the objective function at \(x_*\) is \(4 k^3 / (27 c^2)\text{,}\) which is positive. Therefore the maximum of \(f\) on \([0,\infty)\) is either \(4 k^3 / (27 c^2)\) achieved at \(h = (2k) / (3c)\) or there is no maximum because the function can get arbitrarily large as \(h \to \infty\text{.}\) At infinity, \(f(h) \sim - c h^3\) because \(k h^2 \ll c h^3\) as \(h \to \infty\text{.}\) Therefore, \(h\) has a maximum at a positive location, whose value is \(4 k^3 / (27 c^2)\)
Checkpoint 110.
Continuing the previous example, suppose that for lions \(k = 0.001\) gazelles per square meter, and \(c = 0.0004\) gazelles per cubic meter. What length of lion maximizes its excess food gathering ability, and how many gazelle carcasses per day will be left over for the other lions in the pride?