Unit 2 Variables, functions and graphs
If we count pre-calculus/trigonometry as a pre-requisite, then functions and their graphs are a pre-pre-requisite! But that doesn't mean that you have familiarity with every aspect of these. Recognition of basic types of functions is crucial for being able to use mathematics for modeling and to handle material at the pace and level you will need. So is the ability to go back and forth between analytic expressions for functions and their graphs. So is number sense: knowing approximate values without stopping for a detailed calculation. So is knowledge of how to use physical units in a math problem. We expect most of these to be unfamiliar to many of you, and have included explanations and some homework; this may be challenging, even though it is on pre-college material. We hope it will be at least somewhat interesting!
In addition, there are some more routine things to discuss up front. In order to have a shared language, we need to agree on notation and terminology. Normally it is a good idea to read everything that is assigned; however if this notation is very familiar, you can probably just answer the self-check questions and skip the reading. We apologize for the length of this preliminary section. When the material becomes harder, the sections will be shorter.
Subsection 2.1 Notation and terminology
There are several ways to conceive of a function. One is that it is a rule that takes an input and gives you an output. This is how most of us think of functions most of the time, but it is not precise (rules are sentences which may be ambiguous or underspecified). For this reason we also need a formal definition. A third way to understand functions is via their graphs. We now discuss all three of these ways of characterizing a function, beginning with the most formal.
Definition 2.1.
- A function is a set of ordered pairs with the property that no two ordered pairs have the same first element. The domain of \(f\) is defined to the set of all first elements of the ordered pairs. The range of \(f\) is defined to be the set of all second elements of the ordered pairs.
- The expression \(f(x)\) is defined to equal to \(y\) if the ordered pair \((x,y)\) is in the set of ordered pairs defining \(f\) and undefined otherwise. Informally, \(f(x)\) is called the value of the function \(f\) evaluated at the argument \(x\text{.}\)
Now let's say the same things verbally. The domain of a function is the set of allowed inputs; the range is the set of all outputs. We often name functions with letters; \(f\) is the typical choice, then \(g\) if another is needed, but of course we could name a function anything. While it is common to refer to the function \(f\) as \(f(x)\text{,}\) we will try to observe the distinction that \(f\) is the function and \(f(x)\) is its value at the argument \(x\text{,}\) meaning the output when you plug in \(x\) as an input. The condition that first coordinates are distinct corresponds to the rule producing an unambiguous answer.
Finally, to describe the function \(f\) via its graph, we interpret the ordered pairs as points in the plane, and draw this set as a curve. The condition that first coordinates are distinct corresponds to the so-called vertical line test: any vertical line (vertical lines being sets with a single fixed \(x\)-coordinate but all possible \(y\)-coordinates) intersects the graph at most once.
Why be so formal?
In common usage, one might encounter any of the three ways of defining or referring to a function. We don't want to drown in formality, so we usually use something only as formal as needed. Let's look at why we sometimes need formality.
Example 2.2.
Suppose we define a function \(f\) by \(f(x) := x^2 + 2\text{.}\) Have we formally defined this function? It sounds as if this is the set of ordered pairs
That would be if we meant the domain to be the set of all integers. Maybe instead we meant the domain to be the set of all real numbers. In that case, the "\(\ldots\)" in the list is somewhat misleading; we should probably write the set of ordered pairs like this:
(we use the notation \(\mathbb{R}\) for the real numbers and \(\in\) for the "is an element of"). If this function arose in a word problem where \(f(x)\) represented the value of some quantity at a time \(x\) seconds after the start, maybe it makes sense to allow only nonnegative real numbers as inputs. Formally, this would look like
which could also be written
or
this last version assuming we understood this to mean real numbers at least zero rather than, say, integers at least zero.
A consequence of this discussion is that two functions are technically different if they have different domains, even if they have the same defining rule. We mostly don't care about this distinction unless it matters to some problem, such as trying to determine the number of solutions to an equation, as in the next exercise.
Technically, our discussion of the function \(x \mapsto x^2 + 2\) referred to three different functions: one whose domain was all integers, one whose domain was all reals, and one whose domain is all nonnegative reals. You can see they are different functions: even thought the defining equation \(f(x) := x^2 + 2\) is the same for all three, they are defined by different sets of ordered pairs. On the other hand, for many purposes, we don't care which of these functions was intended. We can feel free to define the function by \(f(x) := x^2 + 2\) without specifying the domain unless and until we get into trouble with the ambiguity in the domain. If we try to answer a question like "How many solutions are there to \(f(x) = 3\text{?}\)" then we will need to be more precise about the domain.
Checkpoint 6.
What are the respective numbers of solutions to \(f(x) = 3\) when \(f (x) := x^2 + 2\) and the domain is. . .
the integers \(\left\{\ldots,-3,-2,-1,0,1,2,3,\ldots\right\}\)
the real numbers \(\mathbb{R}\)
the nonnegative reals \(\left\{x\in\mathbb{R}: x\geq 0 \right\}\)
In the discussion so far, we have introduced four notations you are probably familiar with, but to be completely explicit, we discuss each briefly.
- Maps-to notation.
- Often we name a function when defining it, then refer to it by name, but we can also refer to it using the "maps-to" symbol \(\mapsto\text{.}\) Thus, \(x \mapsto x^2 + 2\) refers to the function that we named \(f\text{,}\) above. We use this when mentioning a function but rarely when evaluating it at an argument because the notation \((x \mapsto x^2 + 2) (3)\) is an atrocity (but technically equal to 11).
- Open and closed interval notation.
-
The interval \([a,b]\) refers to all real numbers \(x\) such that \(a \leq x \leq b\text{.}\) When both endpoints are included, this is called a closed interval.
The interval \((a,b)\) refers to all real numbers \(x\) such that \(a \leq x \leq b\text{.}\) When both endpoints are excluded, this is called an open interval.
Warning 2.3.
The notation for an open interval is exactly the same as for an ordered pair! If there is any ambiguity we will try to specify which, for example, "Let \((a,b)\) be the open interval..."The notations \((a,b]\) and \([a,b)\) are called half-open and refer to an interval with one point (the one next to the square bracket) included and one excluded.
- Set-builder notation.
To define a subset of some set \(S\text{,}\) we write \(\{ x \in S : \cdots \}\) where instead of the three dots we write a property of \(x\) that can be true or false. In some books the colon is replaced by a vertical line, the words "such that" or the abbreviation \(s.t.\) . If the set \(S\) is the set of all real numbers it is sometimes omitted. Thus, for example, \(\{ x : a \leq x \lt b \}\) refers to the half open interval of real numbers, \([a,b)\text{.}\)
- The defining colon-equal sign.
- We use \(:=\) to mean that the quantity on the left is defined to be the quantity on the right, and a regular equal sign to mean an equation that could hold for some values of the variables and fail for others. Thus, \(f(x) := x^2 + 2\) defines a function, whereas \(f(x) = x^2 + 2\) is an equation which is true when a given function \(f\text{,}\) evaluated at \(x\text{,}\) has the same value as \(x^2 + 2\text{,}\) and false otherwise.
Checkpoint 7.
Suppose \(f(x) := x^2 + 2\text{.}\) What values of \(x\) make the equation
true? Please simplify your answer(s).
The range of a function \(f\) is defined to be the set of all possible function values. Formally we can write the range of \(f\) as the set \(\{ f(x) : x \in \text{domain of } f \}\text{.}\)
One final remark about the basic definitions: there is an ambiguity in common usage of the word "range". Sometimes "range" is used to refer to a bigger set than in our definition, namely the set of all things of the type that the function outputs (we'll call this other set the target of the function, should we ever need to refer to it.). For example, they might say that the domain and range of a function \(f(x) := x^2 + 2\) is all real numbers. It's fine to define the domain to be all real numbers, but then technically the range is the set of real numbers that are at least 2. If for some reason we want to tell the person we're talking to that we intend the outputs to always be real numbers, we can say "the target is the real numbers".
Checkpoint 8.
What are two formal mathematical ways of writing the set of real numbers that are at least 2, one using set notation and one using interval notation?
Definition by cases.
As we said, the most familiar way of referring to a function is as a rule for converting input to output. Usually the rule is an equation, such as \(f(x) := C - x \cdot e^x\text{,}\) but the rule could be verbal, for example, "Let \(f(t)\) be the amount in tons of carbon dioxide emitted in \(t\) years." Sometimes we want to talk about functions that are defined by equations, but different ones in different parts of the domain. This is called definition by cases. An example from a recent research paper looks like this:
A number of useful functions can be defined in this way. For example the absolute value of \(x\text{,}\) denoted \(\left\lvert x\right\rvert\text{,}\) may also be defined in cases:
Remark 2.4. Some remarks on defining by cases.
- Note that \(x\) and \(-x\) agree at \(x=0\text{,}\) so we could have grouped zero with either case. When this happens, writing\begin{equation*} |x| := \begin{cases} x \amp x \geq 0 \\ -x \amp x \leq 0 \end{cases} \qquad \end{equation*}emphasizes this. If \(x\) and \(-x\) did not agree at \(x=0\text{,}\) this would be a badly formed definition.
- There is a period following the two example definitions but not the one in the first remark. Why? Because well written math follows rules of basic grammar. These rules can be a little different on occasion, but for the most part, you should expect this text to read in complete sentences, to define variables and functions before using them, and when used within sentences, to connect and flow logically, using connecting words like "and", "because", "therefore", and punctuation such as commas and periods.
Checkpoint 9.
Which of the following defines a function whose domain is all real numbers?
\(\displaystyle f(x) := \begin{cases} x+1 \amp x \gt 2 \\ x-1 \amp x \lt 2 \end{cases}\)
\(\displaystyle g(x) := \begin{cases} x+1 \amp x \geq 2 \\ x-1 \amp x \lt 2 \end{cases}\)
\(\displaystyle h(x) := \begin{cases} x+1 \amp x \geq 2 \\ x-1 \amp x \leq 2 \end{cases}\)
\(\text{Choice 2}\)
Free and bound variables.
In the defining statement \(f(x) := x^2 + 2\text{,}\) it would define the same function if instead we said \(f(u) := u^2 + 2\text{.}\) It is the same set of order pairs, has the same graph, etc. The variable \(x\) (or in the second case, \(u\)) is said to be a bound variable. The bound variable in this case runs over all values in the domain of \(f\text{.}\) A variable that is not bound is free. For example, in the definition \(f(u) := u^2 + c\text{,}\) the variable \(c\) is free. The definition of the function \(f\) depends on the value of \(c\text{.}\) If \(c = 2\text{,}\) it boils down to the previous definition. If \(c=1\) it is a different function. If \(c\) has not been assigned a value, then \(f\) is a function whose range is not the real numbers but rather algebraic expressions in the variable \(c\text{.}\)
Bound variables arise many times throughout this course, in fact throughout math and throughout life! Here is a list of some places bound variables occur in this course, the first two of which you have already seen.
- In the definition of a function
- In the definition of a subset
- In limits
- In the definition of a derivative
- In summations
- In the definition of an integral
- In notions of orders of magnitude and asymptotic equivalence
- In Taylor's theorem
Let's get some practice with identifying free and bound variables.
Definition 2.5.
A function \(f\) is said to be differentiable at \(x\) if \(x\) is in the domain of \(f\) and \(f'(x)\) exists.
Definition 2.6.
A function \(f\) is said to be differentiable on the open interval \((a,b)\) if \((a,b)\) is in the domain of \(f\) and if, for all \(x \in (a,b)\text{,}\) the derivative \(f'(x)\) exists.
Checkpoint 10.
In Definition 2.6, identify which variables are free and which are bound:
\(a\) is
free
bound
\(b\) is
free
bound
\(x\) is
free
bound
Subsection 2.2 Some useful functions
Here are some more useful special functions.
The greatest integer function at the argument \(x\) is denoted \(\lfloor x \rfloor\) defined to be the greatest integer \(y\) such that \(y \leq x\text{.}\) In other words, if \(x\) is an integer then \(\lfloor x \rfloor = x\text{;}\) if \(x\) is positive and not an integer, then \(\lfloor x \rfloor\) is the "whole number you get when you write \(x\) as a decimal and ignore what comes after the decimal point"; if \(x\) is negative and not an integer, it is \(-1\) plus what you get when you ignore the decimals. In older texts, the same function is sometimes denoted \([x]\text{.}\) This square bracket notation has largely been abandonded in favor of the "floor" notation, because (especially in computer science) we also often want to use the ceiling function as well. The ceiling function at the argument \(x\) is denoted \(\lceil x \rceil\) and is defined to be the least integer \(y\) such that \(y \geq x\text{.}\) Informally, \(\lfloor x \rfloor\) rounds down to the nearest integer and \(\lceil x \rceil\) rounds up.
Checkpoint 11.
Compute the following floor values:
\(\lfloor 3\rfloor\)
\(\lfloor 9.4\rfloor\)
\(\lfloor\sqrt{2}\rfloor\)
\(\lfloor 0\rfloor\)
\(\lfloor -1.5\rfloor\)
Compute the following ceiling values:
\(\lceil 3\rceil\)
\(\lceil 9.4\rceil\)
\(\lceil\sqrt{2}\rceil\)
\(\lceil 0\rceil\)
\(\lceil -1.5\rceil\)
Another useful function is the sign function. This is defined by
Another is the delta function, defined by \(\delta (x) = 1\) when \(x = 0\) and \(0\) when \(x \neq 0\text{.}\)
Checkpoint 12.
Write the delta function as a definition by cases.
Subsection 2.3 Properties of functions
We now list certain properties of functions to which we will often refer.
A function \(f\) is said to be odd if \(f(-x) = -f(x)\) for all \(x\) in the domain of \(f\text{.}\) (It is unclear what this would mean if the domain contains \(x\) but not \(-x\text{.}\)) Similarly an even function \(f\) is one satisfying \(f(-x) = f(x)\text{.}\)
Checkpoint 13.
For each of these functions, say whether it is odd, even or neither.
\(f(x) := x^2\) is
odd
even
neither
\(f(x) := 3 - x\) is
odd
even
neither
\(f(x) := x^3 + x\) is
odd
even
neither
\(f(x) := \sin x\) is
odd
even
neither
\(f(x) := \cos x\) is
odd
even
neither
A function \(f\) is said to be increasing if \(f(x) \leq f(y)\) for all values of \(x\) and \(y\) in the domain of \(f\) such that \(x \lt y\text{.}\) Informally, the value of an increasing function gets bigger if the argument gets bigger. If you change the requirement that \(f(x) \leq f(y)\) to the strict inequality \(f(x) \lt f(y)\text{,}\) this defines the notion of strictly increasing. Decreasing and strictly decreasing functions are defined analogously but with one inequality reversed: \(f\) is decreasing if \(f(x) \geq f(y)\) for all \(x,y\) satisfying \(x \lt y\text{.}\)
Checkpoint 14.
We can also say when a function is increasing or decreasing on a part of the domain: \(f\) is increasing on the open interval \((a,b)\) if the above inequality holds for all \(x,y \in (a,b)\text{.}\) For any point \(c \in (a,b)\text{,}\) we then also say that \(f\) is increasing at \(c\text{.}\) In other words, to say \(f\) is increasing at a point \(c\) means there is some \(a \lt c \lt b\) such that \(f\) is increasing on the open interval \((a,b)\text{.}\)
Checkpoint 15.
The sign function is
strictly increasing
increasing
strictly decreasing
decreasing
\(\text{increasing}\)
Subsection 2.4 Graphing
As you already know, points in the plane can be labeled by ordered pairs of real numbers. As you also already know, the graph of a function \(f\) is the set points in the plane corresponding to the ordered pairs \(\{ (x , f(x)) : x \in \text{domain of } f \}\text{.}\)
Often the graph of a function is a continuous curve, and can be quickly drawn, conveying essential information about \(f\) to the eye much more efficiently than if the reader had to wade through equations or set notation.
The following Checkpoint is about the following graphs, borrowed from Hughes-Hallet et al.:
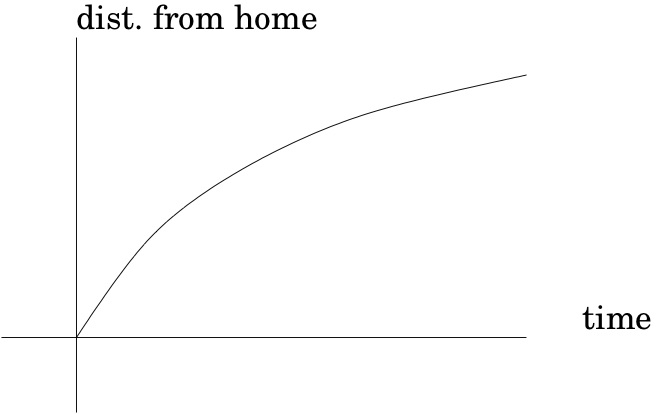
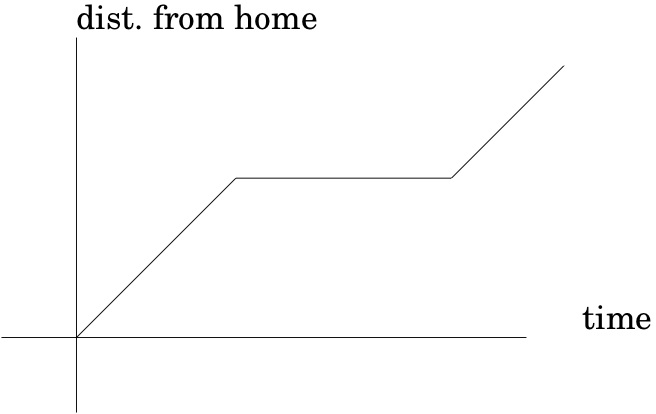
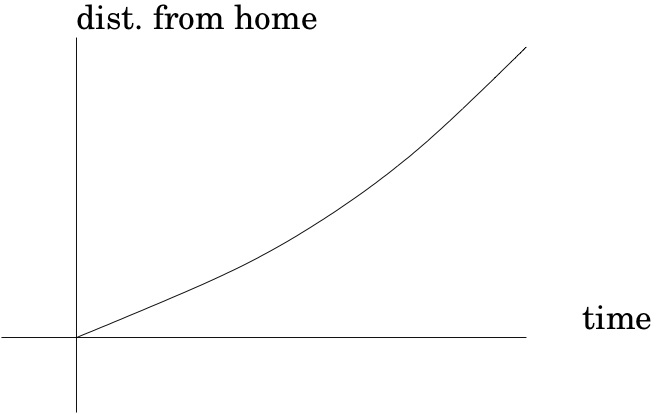
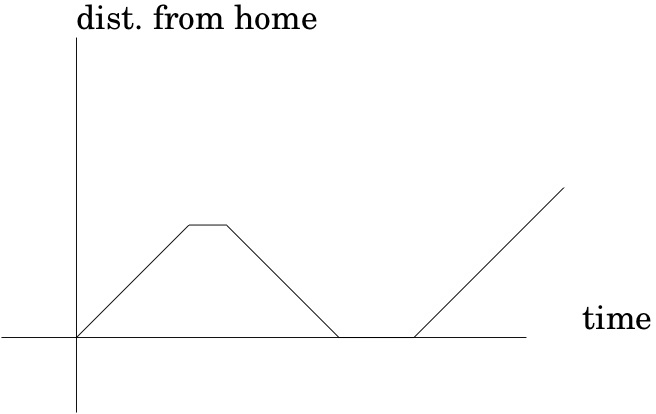
Checkpoint 16.
Number the graphs like this:
1 2
3 4
Which of graph best matches each of the following stories?
I had just left home when I realized I had forgotten my books, so I went back to pick them up.
graph (1)
graph (2)
graph (3)
graph (4)
Things went fine until I had a flat tire.
graph (1)
graph (2)
graph (3)
graph (4)
I started out calmly but sped up when I realized I was going to be late.
graph (1)
graph (2)
graph (3)
graph (4)
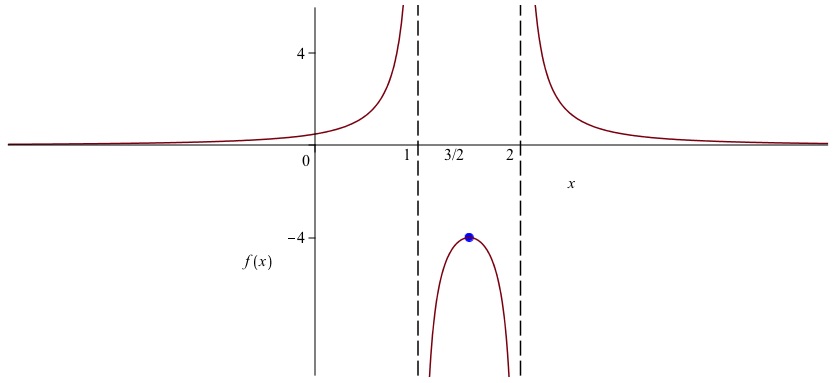
Some conventions make graphs even more effective at conveying information. The axes should be labeled (more on that later) but more importantly, marked so that the scale is clear. Rather than just mark where 1 is on the horizontal and vertical axes, it is often helpful to mark any value where something interesting is going on: a discontuity, an asymptote, a maximum, or a change of cases for functions defined in cases. For example, if we graph \(x \mapsto 1 / (x^2 - 3x + 2)\text{,}\) we should mark vertical asymptotes (a certain kind of discontinuity) on the \(x\)-axis at \(x=1\) and \(x=2\text{;}\) a dashed vertical line is customary. We should mark a local maximum of \(-4\) (marked on the \(y\)-axis) occuring at \(x = 3/2\) (marked on the \(x\)-axis). Another way to do this would be to label and mark the point \((3/2 , -4)\) on the graph. There is a horizontal asymptote at zero, which we would mark with a dashed horizontal line if it occurred anywhere else, but we don't because it is hidden by the \(x\)-axis. When graphing a function on the entire real line, we can't go to infinity and stay in scale, so we either go out of scale or draw a finite portion, large enough to given the idea. Choosing the latter, the resulting picture should look something like the graph in Figure 2.7.
Here follows a list of tips on graphing an unfamiliar function, call it \(f\text{.}\) The last three tips on shifting and scaling are ones we have found in the past that many students vaguely recall but get wrong, so please make sure you know them.
- Is the domain all real numbers? If not, what is it? If the function has a piecewise definition, try drawing each piece separately.
- Is there an obvious symmetry? If \(f(-x) = f(x)\) for all \(x\) in the domain, then \(f\) is even and there is a symmetry about the \(y\)-axis. If \(f(-x) = -f(x)\) then \(f\) is odd and there is 180-degree rotational symmetry about the origin.
- Are there discontinuities, and if so, where? Are there asymptotes?
- Try values of the function near the discontinuities to get an idea of the shape -- these are particularly important places. If the domain includes oints on both sides of a discontinuity be sure to test points on each side.
- Try computing some easy points. Often \(f(0)\) or \(f(1)\) is easy to compute. Trig functions are easily evaluated at certain multiples of \(\pi\text{.}\)
- Where is \(f\) positive?
- Where is \(f\) increasing and where is it decreasing? This will be easier once you know some calculus.
- Where is \(f\) concave upward versus concave downward? This will be a lot easier once you know some calculus.
- Where are the maxima and minima of \(f\) and what are its values there? This will be a lot easier once you know some calculus.
- What does \(f\) do as \(x\) approaches \(\infty\) and \(-\infty\text{?}\)
- Is there a function you understand better than \(f\) which is close enough to \(f\) that their graphs look similar?
- Is \(f\) periodic? Most combinations of trig functions will be periodic.
- Is the graph of \(f\) a shift of a more familiar graph? Graphing \(y = f(x) + c\) shifts the graph up by \(c\text{;}\) this is pretty intuitive; if \(c\) is negative the graph shifts downward. Graphing \(y = f(x+c)\) shifts the graph left or right by \(c\text{.}\) If \(c\) is positive, the graph shifts left.
- Is the graph of \(f\) a rescaling of a more familiar graph? The graph \(y = c f(x)\) stretches vertically by a factor of \(c\text{.}\) When \(c \lt 1\) this is a shrink rather than a stretch.
- The graph of \(y = f(cx)\) stetches or shrinks in the horizontal direction. When \(c \gt 1\text{,}\) it is a shrink. Why? Try sketching \(y = \cos x\) and on top of this sketch \(y = \cos (2x)\text{.}\)
Checkpoint 17.
In vertical stretching, what happens when \(c\) is negative?
Sketch the specific example where \(c = -2\) and \(f(x) = x^2\) on the domain \([-1,1]\)
Checkpoint 18.
In horizontal stretching and shrinking, explain why \(0\lt c\lt 1\) is stretching and \(1\lt c\) is shrinking.
Does this surprise you?
What happens when \(c\) is negative?