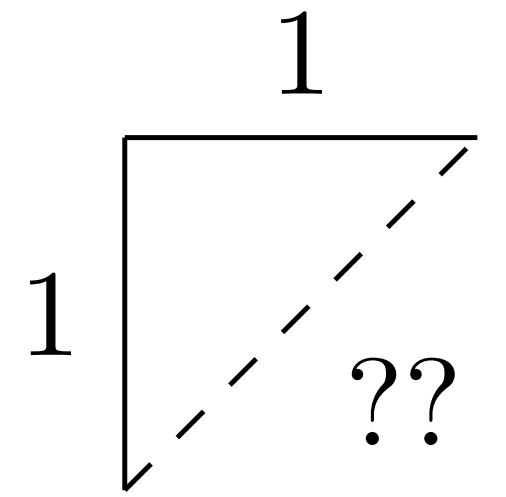Desiderata for a number system

Section 1.1 Desiderata for a number system

Since we get to create the real numbers (as opposed to, say, discovering them somewhere out in the world), we’re in the commander’s chair. So let’s ask ourselves the question

🔗

What would make a number system useful?
🔗

🔗

One way to answer this is to look at what those liebeGottgegeben natural numbers are useful for and what their shortcomings are. Presumably, when we create our new number system $\mathbb{R}\text{,}$ we’d like it to be at least as useful as $\mathbb{N}\text{.}$

🔗

Subsection 1.1.1 number systems and arithmetic

Numbers aren’t interesting just by being there; what makes them useful is the ability to combine them using arithmetic operations. The ones we’ll be interested are addition and multiplication.

🔗

For now

but only for now!

, we’ll take it as given that the natural numbers come equipped with addition and multiplication. The sum of two natural numbers is a natural number, and the product of two natural numbers is a natural numbers. Equipped with the language of the natural numbers and addition, we can start asking questions:

``What is $3+5\text{?}$’’

🔗
``What number can we add to $5$ to get $7\text{?}$’’

🔗
``What number can we add to $9$ to get $5\text{?}$’’

🔗

Notice that the first question is a good deal simpler than the second. The first two questions have answers; but the third does not -- there is no such number. (Any language worth its salt allows us to pose impossible requests and ask unanswerable questions.) In algebraic terms, we’d say that the equation

\begin{equation*} x+9=5 \end{equation*}

has no solution.

🔗

The integers, then, are constructed specifically so that questions like this will be guaranteed to have an answer. On this account, the definition of $-4$ is something like``a number that you can add to 9 and get 5 as a result’’. We’ve augmented our number system $\mathbb{N}$ with a new symbol that stands for the solution of a particular equation. Thus, $\mathbb{N}$ begets $\mathbb{Z}\text{.}$

🔗

Now that we’ve got a number system which has additive inverses, let’s tackle multiplication. We might ask

``What number can we multiply $5$ by to get $65$’’?

🔗
``$-128$ is which multiple of $8\text{?}$’’

🔗
``How many $5$s go into $17\text{?}$’’

🔗

Here again, the first two questions have answers. But the third does not. We would say something like ``17 is not divisible by 5’’.

🔗

The rational numbers are what we invent to solve this problem. The definition of $\frac{17}{5}$ is ``That which, if you multiply it by $5\text{,}$ yields $17\text{.}$", or in algebraic notation, the solution of the equation

\begin{equation*} 5t=17 \end{equation*}

🔗

There’s some subtleties here -- for example, it’s not exactly obvious that the equations

\begin{equation*} 10t=34 \end{equation*}

and

\begin{equation*} -15t=-51 \end{equation*}

have the same solution. But those questions more properly belong in an algebra course.

🔗

Suffice to say that $\mathbb{Q}$ has multiplicative inverse.

🔗

Subsection 1.1.2 algebraic desiderata

If we’re in the business of defining what a real number is, we certainly don’t want to do any worse than the algebraic cleanness of the rationals. So let’s just make a list of those very nice properties that $\mathbb{Q}$ has.

🔗

Definition 1.1.1.

The field axioms are

AC 🔗: For any $a,b\text{,}$ $a+b=b+a\text{.}$
AA 🔗: For any $a,b,c\text{,}$ $a+(b+c)=(a+b)+c\text{.}$
AId 🔗: There is a number $0$ so that, for any $a\text{,}$ $a+0=a\text{.}$
AIn 🔗: For any $a\text{,}$ there is number $-a$ so that $a+(-a)=0\text{.}$
MC 🔗: For any $a,b\text{,}$ $a\cdot b=b\cdot a\text{.}$
MA 🔗: For any $a,b,c\text{,}$ $a\cdot(b\cdot c)=(a\cdot b)\cdot c\text{.}$
MId 🔗: There is a number $1$ so that, for any $a\text{,}$ $a\cdot 1=a\text{.}$
MIn 🔗: For any $a\neq 0\text{,}$ there is number $a^{-1}$ so that $a\cdot (a^{-1})=1\text{.}$
MDA 🔗: For any $a,b,c\text{,}$ $a\cdot(b+c)=(a\cdot b) + (a\cdot c)\text{.}$
ND 🔗: $0\neq 1\text{.}$

🔗

Checkpoint 1.1.2.

The labels I’ve used for these axioms are abbreviations of English phrases. Can you figure out what they stand for?

🔗

Definition 1.1.3.

A set $S\text{,}$ together with two operations $+:S\times S\to S$ and $\cdot:S\times S\to S$ which satisfy the field axioms, is called a field.

🔗

So: $\mathbb{Q}$ is a field, but $\mathbb{N}$ and $\mathbb{Z}$ are not.

🔗

Checkpoint 1.1.4.

Which of the field axioms fail for $\mathbb{N}$ and $\mathbb{Z}$ respectively?

🔗

Checkpoint 1.1.5.

Here is a set with two binary operations. The set is

\begin{equation*} S=\left\{\star,\$\right\} \end{equation*}

The operations are defined by these tables:

$\color{blue}+$	$\color{blue}\star$	$\color{blue}\$$
$\color{blue}\star$	$\$$	$\star$
$\color{blue}\$$	$\star$	$\$$

$\color{red}\cdot$	$\color{red}\star$	$\color{red}\$$
$\color{red}\star$	$\star$	$\$$
$\color{red}\$$	$\$$	$\$$

Prove that these operations define a field.

🔗

Hint.

You’ll need to decide which of $\star,\$$ is 0 and which is 1.

🔗

Fieldiness is pretty useful, algebraically:

🔗

Theorem 1.1.6.

In a field, any linear equation has a unique solution. That is, given a field $S$ and $\alpha,\beta,\gamma\in S$ with $\alpha\neq 0\text{,}$ there is a unique $x\in S$ so that

\begin{equation*} \alpha\cdot x+\beta=\gamma \end{equation*}

🔗

Proof.

Existence.

Since $\alpha\neq 0\text{,}$ there is a multiplicative inverse $\alpha^{-1}\text{.}$ I claim that $x=\alpha^{-1}\cdot \left(\gamma+(-\beta)\right)$ is a solution.

🔗

Let’s just plug in the proposed $x\text{:}$

🔗

\begin{align*} \alpha\cdot x+\beta&=\alpha\cdot \left(\alpha^{-1}\cdot \left(\gamma+(-\beta)\right)\right)+\beta\\ &=\left(\alpha^{-1}\cdot \alpha\right)\cdot \left(\gamma+(-\beta)\right)+\beta\\ &=\left(\gamma+(-\beta)\right)+\beta\\ &=\gamma+\left((-\beta)+\beta\right)\\ &=\gamma+\left(\beta+(-\beta)\right)\\ &=\gamma \end{align*}

Each of these lines, properly speaking, requires a justification from the field axioms -- you should identify which axiom(s) justify each line.

🔗

Uniqueness.

If we had two such, say $x$ and $y\text{,}$ then

🔗

\begin{equation*} \alpha\cdot x+\beta=\gamma=\alpha\cdot y+\beta \end{equation*}

Therefore,

🔗

\begin{align*} \left(\alpha\cdot x+\beta\right)+(-\beta)&=\left(\alpha\cdot y+\beta\right)+(-\beta)\\ \alpha\cdot x+\left(\beta+(-\beta)\right)&=\alpha\cdot y+\left(\beta+(-\beta)\right)\\ \alpha\cdot x&=\alpha\cdot y\\ \alpha^{-1}\cdot \left(\alpha\cdot x\right)&=\alpha^{-1}\cdot \left(\alpha\cdot y\right)\\ x&=y \end{align*}

Here again, each line is supported by either an axiom or by the logical step of "doing the same thing to both sides".

🔗

Subsection 1.1.3 order desiderata

The natural numbers also come with a very clean notion of order. $1$ is less than $2\text{,}$ which is less than $3\text{,}$ &c. This order satisfies the following properties:

Proposition 1.1.7.

For any natural numbers $m,n,p\text{,}$

If $m\lt n$ and $n\lt p\text{,}$ then $m\lt p\text{.}$ ("$\lt$ is transitive")

🔗
Exactly one holds: $m\lt n\text{,}$ $m=n\text{,}$ $n\lt m\text{.}$ ("$\lt$ is total")

🔗

🔗

Proof.

If you attempt to really write down the proof of this statement, you end up realizing that it’s more or less equivalent to the formal definition of the natural numbers. So we’ll take this proposition as an axiom.

🔗

It turns out that this order is compatible with the algebraic operations in the following sense:

🔗

Proposition 1.1.8.

For any natural numbers $m,n\text{,}$ we have

$m\lt m+n\text{,}$ and

🔗
$m\le m\cdot n$ (equality can only happen if $n=1\text{.}$)

🔗

🔗

Aside

🔗

Proof.

The order on the natural numbers is defined by the fact that $m\lt m+1\text{.}$ But $m+n$ just means $(\cdots((m+1)+1)+\cdots+1)+1$ where there are $n$ total $+1$s. So

\begin{equation*} m\lt m+1\lt m+2\lt \cdots\lt m+n\ \ . \end{equation*}

🔗

Now multiplication is just iterated addition; that is,

\begin{equation*} m\cdot n=m+m+\cdots +m \end{equation*}

where there are $n$ total copies of $m$ being added. Applying the first clause of the proposition, we get

\begin{equation*} m\lt m+m\lt m+m+m\lt \cdots \lt m+m+\cdots +m=m\cdot n\ \ \ . \end{equation*}

🔗

$\mathbb{Z}$ inherits this compatibility, as long as we handle the negative numbers properly. The following proposition records this.

🔗

Proposition 1.1.9.

For any $a,b,c\in\mathbb{Z}\text{,}$

If $a\lt b\text{,}$ then $a+c\lt b+c\text{.}$

🔗
If $a\gt 0$ and $b\gt 0\text{,}$ then $a\cdot b\gt 0\text{.}$

🔗

🔗

Proof.

This is an exercise for you! Here are some hints:

You’ll need to use Proposition 1.1.8

🔗
First prove the first clause when $a,b,c\in\mathbb{N}\text{.}$

🔗
Now you’ve got to handle the case some of $a,b,c$ are elements of $\mathbb{Z}\setminus\mathbb{N}\text{,}$ i.e. either zero or negative.

🔗
The case when one of $a,b,c$ is 0 is easy.

🔗
The definition of the ordering on $\mathbb{Z}$ says that $-1\lt 0\text{.}$

🔗
Now for any of $a,b,c$ which is negative, write it as an iterated addition of $-1$s.

🔗

🔗

The order on $\mathbb{Z}$ begets an order on $\mathbb{Q}$ which is compatible with $\mathbb{Q}$’s (similarly begotten) algebraic operations.

🔗

Checkpoint 1.1.10.

Define what we mean by $p\lt q$ if $p,q\in\mathbb{Q}\text{.}$ Your definition must be written in terms of $\mathbb{Z}\text{.}$

🔗

Checkpoint 1.1.11.

Using your definition from Checkpoint 1.1.10, show that Proposition 1.1.9 holds if we take $a,b,c\in\mathbb{Q}\text{.}$

🔗

This compatibility between the order on $\mathbb{Q}$ and the algebraic operations on $\mathbb{Q}$ is so nice that we give it a name:

🔗

Definition 1.1.12.

An ordered field is a set, together with operations $+:S\times S\to S$ and $\cdot:S\times S\to S$ and a binary relation $\lt$ on $S\text{,}$ which satisfy the field axioms and

OTr 🔗: If $m\lt n$ and $n\lt p\text{,}$ then $m\lt p\text{.}$
OTo 🔗: Exactly one is true: $m\lt n\text{,}$ $m=n\text{,}$ or$n\lt m\text{.}$
OCA 🔗: If $a\lt b\text{,}$ then $a+c\lt b+c\text{.}$
OCM 🔗: If $0\lt a$ and $0\lt b\text{,}$ then $0\lt a\cdot b\text{.}$

🔗

Checkpoint 1.1.13.

Show that, no matter what order relation we try to put on it, the field from Checkpoint 1.1.5 cannot be made into an ordered field.

🔗

Hint.

There are only two possible orders we could use -- either $\star\lt \$$ or $\$\lt \star\text{.}$ Show that either way, we violate one of the order axioms in Definition 1.1.12.

🔗

Checkpoint 1.1.14.

Show that any ordered field must contain infinitely many distinct elements.

🔗

Definition 1.1.12 does not explicitly spell out many of the basic facts about inequalities that we learned in grade school. Which means we’d better prove them ourselves using the five order axioms. By way of example:

🔗

Proposition 1.1.15.

In any ordered field, $0\lt 1\text{.}$

🔗

Proof.

By axiom ND, we know $0\neq 1\text{.}$ So by axiom OTo, either $0\lt 1$ or $1\lt 0\text{.}$ We’ll rule out $1\lt 0\text{.}$

🔗

Suppose that indeed $1\lt 0\text{.}$ Let’s use axiom OCA and add $-1$ to both sides:

\begin{align*} 1\amp \lt 0\\ 1+(-1)\amp \lt 0+(-1)\\ 0\amp \lt -1 \end{align*}

🔗

Now axiom OCM can be applied with $a=b=-1$ to see that $0\lt (-1)\cdot(-1)\text{.}$

🔗

On the other hand, we showed above that in any field, $(-1)\cdot(-1)=1\text{.}$ So we’ve gotten to $0\lt 1\text{.}$

🔗

Thus we are in the situation that $1\lt 0$ (by supposition) and $0\lt 1\text{.}$ This violates axiom OTo.

🔗

Having ruled out $1\lt 0\text{,}$ we are left with only the possibility that $0\lt 1\text{.}$

🔗

Checkpoint 1.1.16.

The complex numbers $\mathbb{C}$ are a field in which equations like $x^2+7=0$ can be solved. In particular, there is an element $i\in\mathbb{C}$ which satisfies $i^2=-1\text{.}$ Show that, no matter what order we attempt to use on $\mathbb{C}\text{,}$ it cannot be made into an ordered field.

🔗

Take a look at Checkpoint 1.1.14 and Checkpoint 1.1.16. Checkpoint 1.1.14 tells us that an ordered field cannot be too small. On the other hand, $\mathbb{C}$ is quite a bit larger than $\mathbb{Q}$ -- it contains solutions of many more equations. So while a field can be almost any

It’s a fact of algebra that finite fields can only have a number of elements equal to a power of a prime number.

size, an ordered field can be neither too small nor too large.

🔗

Subsection 1.1.4 What the ordered field axioms buy us

The ordered field axioms (spelled out in Definition 1.1.1 and Definition 1.1.12) certainly are true of $\mathbb{Q}\text{,}$ but are they enough to get us what we need, algebraically speaking?

🔗

We already gave one example, in Proposition 1.1.15, of the ordered field axioms being used to justify "obvious" facts that we probably first learned in grade school. This subsection is a collection point for some others which will end up being useful to us later on. Some I’ve provided proofs for; your job is to figure out the proofs of the others.

🔗

Proposition 1.1.17.

The additive identity is unique. That is, if $x$ and $y$ are elements of the ordered field with $x+y=y\text{,}$ then $x=0\text{.}$

🔗

Proof.

Let’s consider such a pair $x,y\text{.}$ We know that $x+y=y\text{,}$ and we know that there is an additive inverse $-y\text{.}$ Let’s add that additive inverse to both sides:

\begin{align*} x+y&=y\\ (x+y)+-y&=y+-y\\ x+(y+-y)&=0\\ x+0&=0\\ x&=0 \end{align*}

As before, each line is justified by an ordered field axiom. You should identify which is which.

🔗

Proposition 1.1.18.

The multiplicative identity is unique. That is, if $x$ and $y$ are nonzero elements of the ordered field with $y\cdot x=y\text{,}$ then $x=1\text{.}$

🔗

Proposition 1.1.19.

Inverses (of both flavors) are unique. That is, if $a+b=0\text{,}$ then $b=-a\text{;}$ and if $a\cdot b=1\text{,}$ then $b=a^{-1}\text{.}$

🔗

Proposition 1.1.20.

Some statements about how inverses work:

🔗

For any $a\text{,}$ $\left(a^{-1}\right)^{-1}=a$ and $-(-a)=a\text{.}$

🔗
For any $a,b\text{,}$ $-(a\cdot b)=(-a)\cdot b=a\cdot (-b)\text{.}$

🔗
For any $b\text{,}$ $\left(b^2\right)^{-1}=\left(b^{-1}\right)^2\text{.}$

🔗
For any $a,b\text{,}$ $\left(a\cdot b\right)^{-1}=a^{-1}\cdot b^{-1}\text{.}$

🔗

🔗

Proof.

Each of these is a statement that someone’s inverse is someone else. Use uniqueness of inverses by showing that the given formula acts like the inverse it claims to be.

🔗

Proposition 1.1.21.

For any $a\text{,}$ $0\cdot a=0\text{.}$

🔗

Proof.

We know that $0=1+-1\text{.}$ Therefore

\begin{align*} 0\cdot a&=(1+-1)\cdot a\\ &=(1\cdot a)+ \left((-1)\cdot a\right)\\ &=a+(-a)=0 \end{align*}

Going from the second-to-last line to the last line requires one of the statements from Proposition 1.1.20. Which one?

🔗

Proposition 1.1.22. Zero-product principle.

If $x\cdot y=0\text{,}$ then either $x=0$ or $y=0\text{.}$

🔗

Proposition 1.1.23.

For any $a\neq 0\text{,}$ $a^2\gt 0\text{.}$

🔗

In an ordered field, absolute value makes sense:

🔗

Definition 1.1.24.

The absolute value of a number is defined by:

\begin{equation*} \lvert a\rvert =\begin{cases} a& \text{ if }a\geq 0 \\ -a& \text{ if }a\lt 0\end{cases} \end{equation*}

🔗

Proposition 1.1.25.

For any $a\text{,}$

\begin{equation*} a\leq \lvert a\rvert\ \ . \end{equation*}

🔗

Proposition 1.1.26. triangle inequality.

For any $a,b\text{,}$

\begin{equation*} \lvert a+b\rvert\leq \lvert a\rvert+\lvert b\rvert\ \ . \end{equation*}

🔗

Remark 1.1.27.

Proposition 1.1.26 is frequently invoked in the form:

\begin{equation*} \lvert x-y\rvert\leq \lvert x-z\rvert+\lvert z-y\rvert\ \ . \end{equation*}

🔗

Can you see why this form is equivalent to the form given in Proposition 1.1.26? What are the relationships among $a,b,x,y,z\text{?}$

🔗

Subsection 1.1.5 Why $\mathbb{Q}$ isn’t enough

Having axiomatized what’s nice about $\mathbb{Q}$ in the form of Definition 1.1.12, we should realize that actually, $\mathbb{Q}$ is pretty nice!

Aside

🔗

So why not stop there?

🔗

Proposition 1.1.28.

There is no rational number $r$ so that $r^2=2\text{.}$

🔗

Proof.

This is a famous proof, purportedly discovered by Pythagoras himself -- whom (according to the tale) it deeply disturbed.

🔗

Suppose there were some such $r=\frac{p}{q}\text{.}$ We may as well reduce $\frac{p}{q}\text{,}$ so that $p$ and $q$ have no common factors. Our assumption that $r^2=2$ means, in particular, that

🔗

\begin{equation*} p^2=2q^2 \end{equation*}

So $p^2$ must be even. It’s a number-theory fact that if a square is even, then so must be the thing it’s the square of. That is, $p=2k$ for some integer $k\text{.}$ So then

🔗

\begin{align*} (2k)^2&=2q^2\\ 4k^2&=2q^2\\ 2k^2&=q^2 \end{align*}

Again invoking that basic fact of number theory, $q$ is also even.

🔗

But this contradicts the fact that we already reduced the fraction $\frac{p}{q}\text{.}$ So our original supposition must have been incorrect.

🔗

Remark 1.1.29.

Proposition 1.1.28 is frequently stated as "the square root of 2 is irrational". But that’s subtly incorrect, for it assumes that "the square root of 2" is a thing to begin with.

🔗

Besides the obvious algebraic problem that Proposition 1.1.28 poses (contrast to Theorem 1.1.6), it poses a geometric problem:

🔗

Figure 1.1.30. The geometric problem with Proposition 1.1.28.
🔗

🔗

Prev Top Next

\(\color{blue}+\)	\(\color{blue}\star\)	\(\color{blue}\$\)
\(\color{blue}\star\)	\(\$\)	\(\star\)
\(\color{blue}\$\)	\(\star\)	\(\$\)

\(\color{red}\cdot\)	\(\color{red}\star\)	\(\color{red}\$\)
\(\color{red}\star\)	\(\star\)	\(\$\)
\(\color{red}\$\)	\(\$\)	\(\$\)

Section 1.1 Desiderata for a number system

Subsection 1.1.1 number systems and arithmetic

Subsection 1.1.2 algebraic desiderata

Definition 1.1.1.

Checkpoint 1.1.2.

Definition 1.1.3.

Checkpoint 1.1.4.

Checkpoint 1.1.5.

Theorem 1.1.6.

Proof.

Existence.

Uniqueness.

Subsection 1.1.3 order desiderata

Proposition 1.1.7.

Proof.

Proposition 1.1.8.

Aside

Proof.

Proposition 1.1.9.

Proof.

Checkpoint 1.1.10.

Checkpoint 1.1.11.

Definition 1.1.12.

Checkpoint 1.1.13.

Checkpoint 1.1.14.

Proposition 1.1.15.

Proof.

Checkpoint 1.1.16.

Subsection 1.1.4 What the ordered field axioms buy us

Proposition 1.1.17.

Proof.

Proposition 1.1.18.

Proposition 1.1.19.

Proposition 1.1.20.

Proof.

Proposition 1.1.21.

Proof.

Proposition 1.1.22. Zero-product principle.

Proposition 1.1.23.

Definition 1.1.24.

Proposition 1.1.25.

Proposition 1.1.26. triangle inequality.

Remark 1.1.27.

Subsection 1.1.5 Why \(\mathbb{Q}\) isn’t enough

Aside

Proposition 1.1.28.

Proof.

Remark 1.1.29.