Closures and Interiors

Section 3.4 Closures and Interiors

Most sets are neither open nor closed (should we call them ajar?). But given an arbitrary set, we can construct sets that measure (in some sense) how closed or open it is.

🔗

Definition 3.4.1.

We call \(x\) an interior point of the set \(A\) if there is \(\epsilon\gt 0\) so that \(B_\epsilon(x)\subseteq A\text{.}\)

🔗

The set

\begin{equation*} \mathring{A}=\left\{x\ \middle\vert\ x\text{ is interior to A }\right\} \end{equation*}

of all interior points of \(A\) is called the interior of \(A\).

🔗

Proposition 3.4.2.

For any set \(A\text{,}\) \(\mathring{A}\subseteq A\text{.}\)

🔗

Proposition 3.4.3.

\(\mathring{A}\) is open.

🔗

Proof.

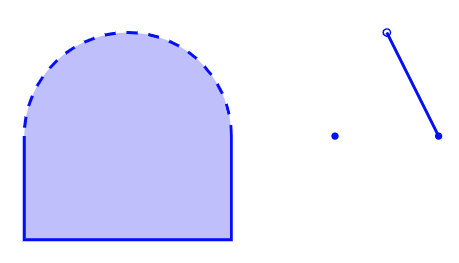
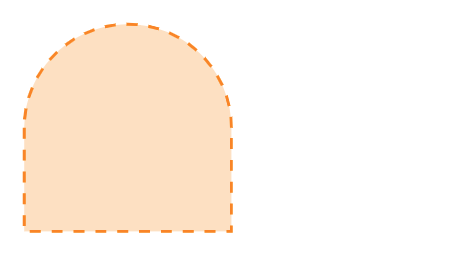
Consider the set

\begin{equation*} A_0=\bigcup\left\{B_\epsilon(z)\ \middle\vert \ z\in A\text{ and } B_\epsilon(z)\subseteq A\right\}\ . \end{equation*}

Clearly \(\mathring{A}\subseteq A'\text{,}\)

🔗

Notice that in order to be in \(\mathring{A}\text{,}\) \(z\) must have an open ball \(B_\epsilon(z)\) around it which also lies in \(A\text{.}\) Moreover, each point of that open ball has a (smaller) open ball around it which lies in \(A\text{;}\) hence the entire ball \(B_\epsilon(z)\) is inside \(\mathring{A}\text{.}\) Therefore \(A_0\subseteq \mathring{A}\text{.}\)

🔗

This shows that \(\mathring{A}=A_0\text{,}\) and \(A_0\) is the union of open sets, hence open.

🔗

Definition 3.4.4.

We call \(x\) a limit point for the set \(A\) if for any \(\epsilon\gt 0\text{,}\) there is a point \(a\in A\) other than \(x\) with \(d(x,a)\lt \epsilon\text{.}\)

🔗

The set of all limit points for \(A\) is denoted \(A'\text{.}\)

🔗

Checkpoint 3.4.5.

Give a characterization of limit point in terms of open sets. That is, say what it means for \(x\) to be a limit point for \(A\text{,}\) which only involves open sets.

🔗

Prove that your version is equivalent to Definition 3.4.4.

🔗

Hint.

The correct answer begins "For any open set \(U\text{,}\) . . .".

🔗

Checkpoint 3.4.6.

In Definition 3.4.4, we could replace "a point of \(A\) other than \(x\)" with "infinitely many points of \(A\)".

🔗

Definition 3.4.7.

The set

\begin{equation*} \overline{A}=A\cup A' \end{equation*}

is the closure of \(A\text{.}\)

🔗

Figure 3.4.8. A subset \(A\subseteq \mathbb{R}^2\) (blue), its interior (orange), its limit points (red), and its closure (dark red).
🔗

Checkpoint 3.4.9.

Compute \(\mathring{A}\text{,}\) \(A'\) and \(\overline{A}\) for each of these sets \(A\text{:}\)

🔗

\(\displaystyle A=(-2,3)\subseteq \mathbb{R}\)

🔗
\(\displaystyle A=[-2,3]\subseteq\mathbb{R}\)

🔗
\(\displaystyle A=\mathbb{Q}\subseteq\mathbb{R}\)

🔗
\(\displaystyle A=\mathbb{N}\subseteq\mathbb{R}\)

🔗
\(A=\left\{(x,y)\middle\vert y\lt 0\right\}\subseteq\mathbb{R}^2\) (use the standard 2-norm)

🔗
\(A=\left\{(x,y)\middle\vert x\neq y \right\}\subseteq\mathbb{R}^2\) (use the standard 2-norm)

🔗
\(A=\left\{p(x)\middle\vert p\text{ is a polynomial with rational coefficients}\right\}\subseteq \left\{q\middle\vert q\text{ is a polynomial with real coefficients}\right\}\) (use the sup-norm on \([-1,1]\))

🔗