Section 3.4 Closures and Interiors
Most sets are neither open nor closed (should we call them ajar?). But given an arbitrary set, we can construct sets that measure (in some sense) how closed or open it is.
Definition 3.4.1.
We call \(x\) an interior point of the set \(A\) if there is \(\epsilon\gt 0\) so that \(B_\epsilon(x)\subseteq A\text{.}\)
The set
of all interior points of \(A\) is called the interior of \(A\).
Proposition 3.4.2.
For any set \(A\text{,}\) \(\mathring{A}\subseteq A\text{.}\)
Proposition 3.4.3.
\(\mathring{A}\) is open.
Proof.
Consider the set
Clearly \(\mathring{A}\subseteq A'\text{,}\)
Notice that in order to be in \(\mathring{A}\text{,}\) \(z\) must have an open ball \(B_\epsilon(z)\) around it which also lies in \(A\text{.}\) Moreover, each point of that open ball has a (smaller) open ball around it which lies in \(A\text{;}\) hence the entire ball \(B_\epsilon(z)\) is inside \(\mathring{A}\text{.}\) Therefore \(A_0\subseteq \mathring{A}\text{.}\)
This shows that \(\mathring{A}=A_0\text{,}\) and \(A_0\) is the union of open sets, hence open.
Definition 3.4.4.
We call \(x\) a limit point for the set \(A\) if for any \(\epsilon\gt 0\text{,}\) there is a point \(a\in A\) other than \(x\) with \(d(x,a)\lt \epsilon\text{.}\)
The set of all limit points for \(A\) is denoted \(A'\text{.}\)
Checkpoint 3.4.5.
Give a characterization of limit point in terms of open sets. That is, say what it means for \(x\) to be a limit point for \(A\text{,}\) which only involves open sets.
Prove that your version is equivalent to Definition 3.4.4.
The correct answer begins "For any open set \(U\text{,}\) . . .".
Checkpoint 3.4.6.
In Definition 3.4.4, we could replace "a point of \(A\) other than \(x\)" with "infinitely many points of \(A\)".
Definition 3.4.7.
The set
is the closure of \(A\text{.}\)
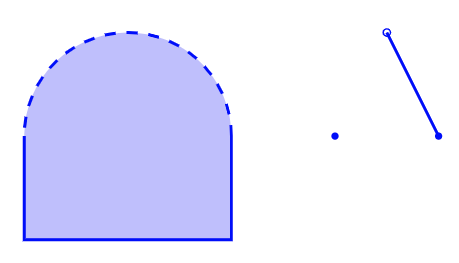
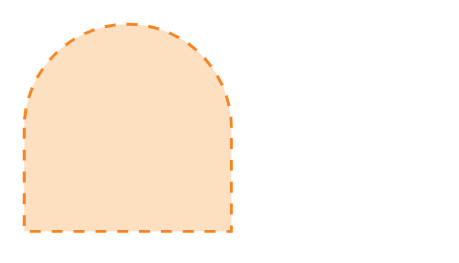


Checkpoint 3.4.9.
Compute \(\mathring{A}\text{,}\) \(A'\) and \(\overline{A}\) for each of these sets \(A\text{:}\)
\(\displaystyle A=(-2,3)\subseteq \mathbb{R}\)
\(\displaystyle A=[-2,3]\subseteq\mathbb{R}\)
\(\displaystyle A=\mathbb{Q}\subseteq\mathbb{R}\)
\(\displaystyle A=\mathbb{N}\subseteq\mathbb{R}\)
\(A=\left\{(x,y)\middle\vert y\lt 0\right\}\subseteq\mathbb{R}^2\) (use the standard 2-norm)
\(A=\left\{(x,y)\middle\vert x\neq y \right\}\subseteq\mathbb{R}^2\) (use the standard 2-norm)
\(A=\left\{p(x)\middle\vert p\text{ is a polynomial with rational coefficients}\right\}\subseteq \left\{q\middle\vert q\text{ is a polynomial with real coefficients}\right\}\) (use the sup-norm on \([-1,1]\))
Proposition 3.4.10.
A set \(A\) is closed if and only if it contains all its limit points.
Remark 3.4.11.
Proposition 3.4.10 applies, in particular, to sets which have no limit points.
Proposition 3.4.12.
If \(A\) is closed, then \(A=\overline{A}\text{.}\)
Proposition 3.4.13.
The closure of any set is closed.
Remark 3.4.14.
So we've constructed, for any set \(A\text{,}\) sets \(\mathring{A},\overline{A}\) so that
and \(\mathring{A}\) is open and \(\overline{A}\) is closed. We can think of these as measuring how far from being open or closed \(A\) is.