robert ghrist


CURRENT PROJECTS
TORSORS:
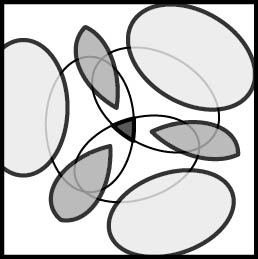
Impossible objects (or visual paradoxes) are explained by cohomology (going back to Penrose). By using network/cellular sheaves, we can identify exactly the mechanism by which visual paradox operates. Torsors with structure sheaves are the perfect language for identifying local relative changes; their classification via cohomology leads to a new understanding of visual paradox. This extends to higher cohomology and novel classes of paradoxes: visual, mechanical, and more. Applications to data science flow naturally as obstructions to sync.
FINANCIAL NETWORKS:
Networks of liabilities and clearing problems are usually solved via classical tools (linear programming / optimization). By recasting clearing in terms of global sections, we can generalize liabilities in financial networks to lattice-valued and other rich categorical data structures.
LATTICE-VALUED CELLULAR SHEAVES:
Cellular sheaves taking values in vector spaces are well-understood, thanks to, e.g., Curry, Hansen, and others. Working with data in different categories can be a challenge. Current work [w/Hans Riess, Paige Randall-North, and Miguel Lopez] involves defining and interpreting sheaf cohomology for cellular sheaves taking values in categories of lattices. In particular, the Tarski Laplacian is a compelling tool for lattice-valued consensus, signal processing, opinion dynamics, and more.
LAPLACIANS & HODGE THEORY FOR SHEAVES:
The graph Laplacian is a fantastic source of perspectives and techniques in network science, data analysis, and geometry: it is also the simplest sort of Hodge Laplacian corresponding to a constant sheaf over a graph. Laplacians exist for sheaves of inner product spaces over cell complexes, and are full of great research threads. Current work [w/Jakob Hansen] involves the creation of spectral sheaf theory and distributed optimization. This has some very recent applications to opinion dynamics over social networks.
POSSIBLE & IMPOSSIBLE MECHANISMS:
Sheaves and cosheaves of vector spaces have the ability to simplify and clarify complex systems of all sorts. One example is in graphic statics, where the classical theory of Maxwell, Cremona, and others can be quickly and cleanly derived from the homology and cohomology of cosheaves and sheaves. Joint work with Zoe Cooperband shows how it's possible to do graphic statics with sheaves and cosheaves not only for mechanisms in 2-D and 3-D, but also for impossible objects.
TIME SERIES DATA:
The signed area between two time series is a simple way to infer lead-lag relationships for cyclic data (data that is periodic up to a time-reparametrization). This ties in to an old theory of K.-T. Chen on iterated integrals and the path signature currently used in rough paths theory. Current work [w/Darrick Lee] focuses on topological and geometric aspects of path signature.
HOMOLOGICAL PERSISTENCE & TDA:
The need for efficient [in time and memory] computation of co/homology is ever-pressing, given the recent revolution in topological data analysis. There are particular challenges in computing persistent co/homology and sheaf cohomology, with the need to extract not only barcodes, but explicit generators. Previous work uses a combination of discrete Morse theory, efficient numerical linear algebra, and matroid theory, with applications to neuroscience data. Current work [w/Greg Henselman-Petrusek] uses homological algebra in nonabelian settings involving lattices and p-exact categories to obtain generators and barcodes with functoriality via saecular persistence. Recent work [w/Iris Yoon] involves cosheaves for distributed persistence computation, and with Yoon and Chad Giusti, matching theorems for bars from data. .
HOMOLOGICAL PROGRAMMING:
There is a topological "core" to all optimization problems. For example, Von Neumann's original minimax theorem was proved using the Brouwer fixed point theorem; Nash's subsequent improvement used an improved fixed point theorem. How much of modern optimization theory can be reduced to or extended via algebraic topology? Perhaps a great deal. The classical max-flow-min-cut theorem has a sheaf-theoretic version [Sanjeevi Krishnan] that connects LP duality with Poincare duality. Recent work [w/Jakob Hansen] sets up homological programming as a topological version of linear programming -- trying to solve optimization problems with (co)homological constraints. This is especially interesting in the context of sheaves.
PAST PROJECTS
TOPOLOGICAL TARGET TRACKING:
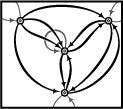
Sheaves and sheaf cohomology (and their duals, cosheaves and cosheaf homology) are extremely useful in solving local-to-global problems in many contexts. One of the more interesting uses is in target-tracking, where sheaves of semigroups over the time-axis can encode the directionality constraints in pursuit-evasion games. Better still is the use of sheaves over more general posets to fuse different types of sensor data, converting detection-based tracking into a coverage problem for co/homology.
TOPOLOGICAL SIGNAL PROCESSING:
Much of the work in radar signal processing depends sensitively on geometry; what can you do with data that is too coarse or noisy to retain geometry well? What if the only available information is topological in nature? We are developing tools for a topological signal processing, including Euler integration (a topological alternative to Riemann integrals), nerve complexes for signals, and modal Lyusternik-Schnirelman categories. All of these tools are relevant to understanding and reconstructing data from topological signals.
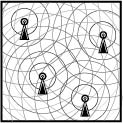
ALGEBRAIC TOPOLOGY AND SENSOR NETWORKS:
As technology for sensors progresses, we will be able to replace large, expensive sensors with swarms of small, cheap, local sensors. One problem facing the sensors community is how to integrate local data into a global picture on an environment and how to manage the information overload. Imagine, for example, that you have thousands upon thousands of mobile video cameras and one of them catches something important. How should the system self-organize to trap the event? And, to make it interesting, lets assume that you do not have GPS, range finders, orientation sensors, or a compass. What now?
Fortunately, topologists solved a similar problem of going from local combinatorial data to a global picture (about a hundred years ago). Homology & cohomology are surprisingly effective at answering questions about coverage and other problems in sensor networks. Recent advances in computational homology and persistent homology make these classical theories newly relevant to a wide variety of problems in security and communication. Sheaf theory is surprisingly useful in data aggregation problems over networks: a simple sheaf-theoretic integral using the Euler characteristic as a measure is very effective in problems of target enumeration over networks, and problems of information flow capacities reduce to sheaf cohomology.
GEOMETRIC / TOPOLOGICAL ROBOTICS
Robotics is an ideal domain for a mathematician to work in: here, one has a genuine need for rigor. Imagine trying to verify that a control system for a robotic brain surgeon works. Would you prefer to have a successful computer simulation or a theorem guaranteeing performance? (Answer: get both if you can...) Using methods and ideas from topology and geometric group theory yields rigorous results about robot motion-planning and control. Examples include spaces of nonpositive curvature as applied to metamorphic and reconfigurable robots, and also to robot coordination problems. CAT(0) geometry answers questions about pursuit-evasion algorithms and optimal multi-agent planning. These ideas also have strong overlap with work in self-assembly, especially the programmable kind.
CONTACT TOPOLOGY AND FLUID DYNAMICS
Rigorous results about fluid dynamics are rare for fully three-dimensional flows. I use global techniques from contact topology (an odd-dimensional variant of symplectic topology) to prove results about the most difficult classes of steady inviscid fluid flows. These techniques, e.g., contact homology, can be used answer questions about concrete physical phenomena such as hydrodynamic instability.
KNOTS, LINKS, & BRAIDS IN DYNAMICS
One of the ways in which topological methods most directly impact applications is via differential equations: much of the history of dynamical systems theory traces back to topological perspectives. I have contributed to the relationships between knot theory and dynamics. One way in which these fields interact arises whenever you have a vector field on a three-dimensional domain: periodic orbits naturally trace out simple closed curves. In what ways do the knotting and linking data reflect or indeed force dynamical data? There is a rich theory here, including simple examples of differential equations for which the most chaotic types of knotting imaginable are present: all knots and links are present as structurally stable periodic orbits. Recent work has focused on applications of braid theory to scalar parabolic PDEs via a topological version of the comparison principle. This involves using Conley's version of Morse theory, leading to a Floer homology for dynamical braids.
