Rigid Motions. Rigid motions are perhaps the simplest transformations in graphics. A rigid motion F(X) simply preserves the distance between any two points:
translations, such as (x1, x2) --> (x1 - 3, x2 + 1), which translates every point by (-3, 1).
rotations, such as the +90 degree rotation: (x1, x2) --> (-x2, x1).
reflections, such as across the horizontal axis: (x1, x2) --> (x1, -x2).
In the notes
Markov Chains.
we show that for these transition all of the eigenvalues of M satisfy
|eigenvalue| <= 1. Moreover, if all the elements of M are strictly
positive, then all the eigenvectors other than those of the form
cP1 satisfy |eigenvalue| < 1 and the matrices
Mk converge as k gets large.
This convergence is easy to prove if one can diagonalize M.
| back to table of contents |
Leonteif input-output matrix This is an important application in economics. Here one also meets matrices all of whose elements are non-negative. See the printed lecture notes from the book by Strang that I distributed in class (it also has more on Markov chains).
Data. We begin a new segment of the course discussing some aspects of data. The first example is Sex Bias in Graduate Admissions? . It illustrates Simpson's paradox, which arises when summarizing data too hastily. The key question to ask is, "does the summary weigh the component data adequately?".
Some obvious examples of rigid motions from the plane R2 to itself that leave the origin fixed are rotations and reflections. In fact, these are the only possibilities. For maps of R2 to itself (and also in higher dimensions), it is less obvious what a "rotation" means. [continued next Wednesday].
We can write any vector X as X = PX + (I-P)X. Let W = PX and Z = (I-P)X. Clearly PW =P2X = PX = W and PZ = P(I-P)X =(P - P2)X = 0.
Rat in a two room maze.
Say that Room 1 opens to the outside, and if a rat enters that room,
it simply leaves the maze.
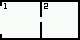If the rat is in Room 2, the door to Room
1 opens every hour and there is a 70% chance that the rat will stay
Room 2. If the rat starts in Room 2, what is the expected waiting
time until it goes to Room 1?
To solve this, for simplicity let p = .70. We compute the expected
time spent in Room 2. Since the rat starts in Room 2, then it
certainly spends the first hour there, but there is only a probability
of p that it spends the second hour in Room 2. Similarly there is a
probability of p2 that it spends the third hour there, etc.
Consequently, the expected time T spent in Room 2 is
There is another way to reach the same conclusion. Again, let T be the expected waiting time to go to Room 1. The rat starts in Room 2. With probability p the rat will be in Room 2 for the second hour. But then the process is back at its starting point and the rat will wait T additional hours before entering Room 1. Thus
Data (continued) Say at times t1, t2,...,t13 we get the 13 pieces of data q1, q2,...,q13. To understand the data we plot it -- and observe that it looks like it approximately fits a straight line q = at + b. How can we find the values of the coefficients a and b that best fit this data? A standard approach is to use the method of least squares. For this we measure the error
| back to table of contents |
- G(X) = RX for some matrix R.
- ||RX - RY|| = ||X - Y|| for all X and Y (obvious from the Property of G(X)).
- ||RX|| = ||X || (the special case Y = 0 from above).
- <RX, RY>= <X, Y> (square both sides of Property 2, then use ||Z||2 = <Z, Z> and the algebraic properties of the inner product).
- R*R = I, that is, R* = R-1. This is proved using Property 4 and the definition of the adjoint, R*.
- The columns of R are unit vectors and they are mutually orthogonal. To show this, one uses, for instance, that the 2nd column of R is just Re2, where e2 = (0,1,0,...,0). Then use Property 4 where X and Y are the vectors e1, e2, etc.
- If c is an eigenvalue of R, then |c| = 1. (Proof: Say RV = cV for come constant c and some non-zero vector V. Then by Property 3, ||V|| = ||RV|| = ||cV|| = |c| ||V||, so |c| = 1.)
- det(R) = +1 or -1. (Proof: We use that for square matrices A, B then det(AB) = det(A) det(B) and det(A*) = det(A). Then 1 = det(I) = det(R*R) = det(R*) det(R) = [det(R)]2. Thus det (R) = +1 or -1.)
We show that in 2 dimensions, every 2 × 2 orthogonal matrix with det R = +1 is a rotation, so
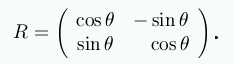
If det R = -1, the same holds if we switch the signs in one column, say the last column. Geometrically this just includes a reflection.
In 3 dimensions, by using a preliminary reflection we may assume that det R = +1. Then by a brief argument one shows that +1 is an eigenvalue of R. This implies there is some (non-zero) vector V with RV = V. Thus, this vector is unchanged by R so R only acts in the plane perpendicular to V. Since this plane is two dimensional, by the previous paragraph we conclude that R is simply a rotation of this plane leaving V fixed, so R is a rotation with axis V.
These rigid motions are essential is any computer graphics. As an example, you may find it illuminating to look at the following Maple program that seeks understanding of how the number of hours of daylight on earth depends on the day of the year and on your latitude. The key ingredient is that the earth rotates around the sun roughly every 365 days, and that its axis is tilted from the vertical plane defined by the earth's orbit around the sun. Hours of Daylight (uses Maple).
| back to table of contents |
Let X and Y be random variables. Here are some standard properties.
- E(X+c) = E(X) + c
- E(aX) = aE(X)
- E(X+Y) = E(X) + E(Y)
- Var(X) = E[(X-E(X)]2) = E(X2) -E(X)2
- SD(X) = sqrt[Var(X)]
- Var(X+c) = Var(X)
- Var(aX) = a2Var(X) so SD(aX) = |a|SD(X).
- Var(X+Y) = Var(X) +Var(Y) +2[E(XY) - E(x)E(Y)]
- In particular, if X and Y are independent, then E(XY) = E(x)E(Y) so
Var(X+Y) = Var(X) +Var(Y)
As a special case, if X and Y have the same standard deviation =Sd, then Var(X+Y) = 2Sd2 and SD(X+Y) = sqrt{2}Sd - More generally, if X1, ... , Xk are
independent and have the same standard deviation = Sd, then,
Var(X1 + ... + Xk) =kSd2 so
SD(X1 + ... + Xk) =sqrt(k)Sd
Thus by property 7 above, we have the following square root law for the standard deviation of an average of independent variables that have the same standard deviation Sd:
SD((X1 + ... + Xk)/k) = Sd/sqrt{k}
Example: One die has 6 possible faces. Let the random variable X
assign to each throw of the die the number that appears. Then the
expected value E(X) = 7/2 = 3.5 and Var(X) = 2.9166. Then SD(X) =
sqrt{2.9166} = 1.71.
If you throw two die, let the random variable W be the sum of the
numbers, W = X1 + X2 of each die. Since we just
computed the expected value and variance if the X1 and
X2 using X in the previous example, we can use the above
properties to find them for W: E(W) = E(X1 + X2)
= 2(7/2) = 7, while similarly, using Property 9 then Var(W) = 2Var(X) =
(2.9166) = 5.8332 and SD(W) = sqrt(2)SD(X) = sqrt(5.8332) = 2.42.
If we let Y be the average of the sum on these two dice, then Y =
(1/2)W so SD(Y)= sqrt(1/2)SD(X) = 1.21.
Example: Say you have a box with only two different numbers,
j of them are a"s and k of them are b's. If you take one random number
from the box and let the random variable X be the number you get, what is its
expected value? What is the standard deviation?
Solution: Since there are j+k numbers, the expected value is
m := E(X) = (ja + kb)/(j+k). The variance is
Var(X) = [j(a-m)2 + k(b-m) 2]/(j+k).
After substituting the value of m and collecting terms you find
that Var(X) =(b-a)2[p(1-p)], where p = j/(j+k) is the
percentage of a's in the box = the probability of getting an "a", while
1-p = k/(j+k) is the probability of getting a "b". Consequently,
SD(X) = |b-a|sqrt{p(1-p)}.
The essence is a gif image that consists of several different images "glued" together as several frames of a single graphic.
There are several steps to make such images:
0. Turn off the computer and think through your design. What do you want create? Ideally, what should it look like? Make sketches. This design phase is the most difficult and creative step.
1. Turn on the computer. Use a "paint" program to create each of the separate frames in your design.
2. Use some utility to collect these frames into a single moving image.
3. Use a utility to have this image play in a loop as many times as you wish.
4. Insert your image into a web page.
| back to table of contents |
Voting on the Web.How can you arrange for a group of people to vote on something using the Web?
dx/dt = cx
If c > 0 one has exponential growth, while if c < 0 exponential decay. One can measure the constant c experimentally say, by measuring when one has double (or half) the initial amount.
dx/dt = cx(M - x), c>0 and M>0 are constants [logistic equation] Although one can solve this explicitly by "separation of variables" integrating the result using partial fractions, one gets more insight into the qualitative behavior by understand the function f(x) = cx(M - x), plotting y = f(x). Note that the points xj where f(x) = 0 are equilibrium solutions of the equation.
There are three qualitatively different cases to understand: x(0) <0, 0 < x(0) < M, and x(0) > M.
| back to table of contents |