If you roll two dice, what is the likelihood of at least one face being a 2? What is the likelihood of the sum being 5?
Birthday Problem: There are 25 people in a room. What is the likelihood that at least two of them have the same birthday? What is the probability P that exactly two of them have the same birthday? The new idea in this problem is that computing probabilities involving or is usually much more complicated than those using and . We compute the probability Q that none of the 25 people have the same birthday. Then P = 1 - Q.
One reference for this lecture is Chapters 1 and 3 of M. Grinstead, Charles M. and J. Laurie Snell, Introduction to Probability. See Math 210 Bibliography for pdf files with these chapters. If you find these useful, you may want to buy the printed book.
| back to table of contents |
Viewing pages others have created by using View Page Source on your Web Browser.
A Simple Web Page A More Complicated Example.
A Few Unix commands
(to be added: copying files and moving them to other directories)
| back to table of contents |
If you roll one die 4 times, what is the probability of getting at least one 6?
If you roll two dice 17 times, what is the probability of getting at least one pair of 6's?
| back to table of contents |
General Answer: If you have n "letters" there are n!/(n-k)! words with exactly k letters. For this example there are 5!/(5-3)! =60. words.
Indistinct Objects: The same question, only now the order of the
k letters is irrelevant. Since there are 3! ways of rearranging three
letters, now there are only 60/3! = 10 sets with three different letters.
General Answer: If you have n "letters" there are
n!/[k!(n-k)!] sets with exactly k letters. This is is the binomial
coefficient:
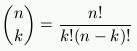
Binomial Probabilities: A biased coin is tossed five
times. Say there is a probability p of heads and thus q=(1-p) of tails.
Say you win if exactly three of the tosses give heads. Thus you win
with any the sequences HHHTT, HHTHT, etc.
There is a probability of p3q2 of the
winning sequences HHHTT, and similarly for any of the other winning
sequences HHTHT, etc. Since from the previous paragraph
there there are 5!/[3!(5-3)! = 10 different winning sequences, the
probability of winning is 10p3q2.
In general with n trials, each having a success probability p, the probability of exactly k successes is
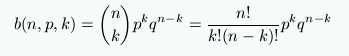
See Grinstead and Snell Chapter 3
Grinstead and Snell, Chapter 3 (pdf)
| back to table of contents |
| back to table of contents |
Example: June 1, 2001 We need to observe that June 1 is the 152nd day in 2001 (since 31+28+31+30+31+1 = 152) so it is 152-1 = 151 days after Jan. 1. Because 151 = 21*7 + 4, we know the day is 4 days later, a Friday.
Example: June 1, 2017 We know that 16 full years have elapsed making 16*365 days, to which we need to add 4 days for the leap years 2004, 2008, 20012, and 2016. Finally, as above we add 152-1=151 to compute that N = 16*365 + 4 + 151 days have elapsed since Jan. 1, 2001. To determine the day of the week we need only the remainder when dividing N by 7. It is 3 so the day is three days after Monday: a Thursday.
To check these computations, on a Unix computer the command cal 2017 gives a calendar for the year 2017, while cal 6 2017 gives a calendar for June 2017.
Conditional Probabilities
See
The Legacy of the Reverend Bayes and
Grinstead and Snell, Chapter 4 (pdf)
Baysean Inference -- Tutorials and Resources
| back to table of contents |
Although most computers do not allow you to have programs on the web, our class does allow this. However, for security, they can only be in the directory html/cgi-bin/ (or its sub-directories).
Any programs on the web must allow anyone to execute them. On a Unix computer this usually means
Programs not intended for the web can be located in any of your directories. You may wish to make a directory 210 for our class stuff:
mkdir $HOME/210Although we will primarily use Perl in class, please feel free to use any other computer language you may prefer. Just don't assume that I will be able to help you with it.
A simple Perl example. This will also run on mail.sas or eniac.seas, except that you may need to change the location of perl. [To find the location just type which perl.]
A
Web form that collects input for
an addition Perl program. This is essentially identical to the previous
line, except using the Web for input.
Another example using the Web for input
A similar script, only using JavaScript instead of Perl. This is
entirely self-contained. View the Page Source to see the details.
adding,
using JavaScript.
See Voting on the Web for a sequence of Perl examples I wrote for this class.
See also
Math 210 Bibliography for some useful online Perl references.
| back to table of contents |
ask the user: input: ask
command line input: program command line
Copy these programs to your own directory and try them. Remember to change the permissions so these programs are executable: chmod 755 [name_of_program] .
- Some Perl examples:
- test for equality of numbers: if ($x ==3 ) {$y = 2 };
- test for equality of strings:
if ($name eq "Brian") {print "\n\tHi $name\n"; } - integer division remainder: (19 % 4) gives the remainder when dividing 19 by 4.
- integer part of a number: int(17.34) gives 17 .
Note int(-17.34) gives -17, which may not be what you want (int always rounds toward 0). Use floor to get rounding to the next lower integer. Thus floor(-17.34) gives -18. Since floor is not a standard part of perl, before using it you need to have one line with the following:
use POSIX "floor"; - Random numbers. $x = rand(6) assigns $x a random real number
0 <= $x < 6 .
To simulate random heads/tails you can use $toss = int(rand(2)), where 0 means Heads and 1 Tails.
To simulate a roll of a die, try $roll = int(rand(6)) +1.
Conditional probability (more). A tree diagram is often useful
when analyzing a situation involving conditional probability.
See the discussion in Section 4.1 of
Grinstead and Snell, Chapter 4 (pdf)
| back to table of contents |
Day of the week. Here is one version. It asks for the date.
Day of Week (perl)
If one cleans up, this appears much shorter (but less clear):
Day of Week
The computation of binomial probabilities (see Jan. 23)
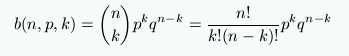
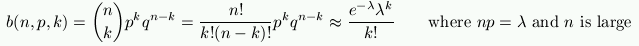
See also Chapter 5 of Grinstead and Snell.
| back to table of contents |
| back to table of contents |
Computer graphics using matrices -- and an example using Maple: The Letter F (see also F page 1 and F page 2).
| back to table of contents |
An introduction to Markov Chains.
Here is a typical (simple) example:
There are two local branches of the Limousine Rental Company, one at the Airport and one in the City, as well as branches Elsewhere.
Say every week of the limousines rented from the Airport 25% are returned to the City and 2% to branches located Elsewhere. Similarly of the limousines rented from the City 25% are returned to Airport and 2% to Elsewhere. Finally, say 10% of the limousines rented from Elsewhere are returned to the Airport and 10% to the City.
If initially there are 35 limousines at the Airport, 35 in the City, and 150 Elsewhere, what is the long-term distribution of the limousines?
| back to table of contents |