Convexity
1. Convexity Defined
Definition
A real-valued function \(f\) defined on some interval \(I\) is called convex when for any points \(p_1,p_2 \in I\), the secant line joining \((p_1,f(p_1))\) to \((p_2,f(p_2))\) lies above the graph \(y = f(x)\) for all \(x\) between \(p_1\) and \(p_2\). In other words, \(f\) is convex on \(I\) when for any \(p_1,p_2 \in I\) and any \(t \in [0,1]\),
\[{}f( (1-t)p_1 + t p_2){}\]
\[{}\leq (1-t) f(p_1) + t f(p_2).{}\]
Example
The function \(f(x) = x^2\) is convex on the real line. This is because
\[{}((1-t) p_1 + t p_2)^2{}\]
\[{}= (1-t)^2 p_1^2 + 2 t(1-t) p_1 p_2 + t^2 p_2^2{}\]
\[{}= (1-t) p_1^2 + t p_2^2{}\]
\[{}+ ((1-t)^2-(1-t)) p_1^2{}\]
\[{}+ 2 t(1-t) p_1 p_2 + (t^2 - t) p_2^2{}\]
\[{}= (1-t) p_1^2 + t p_2^2 + (t^2-t) p_1^2{}\]
\[{}+ 2 t(1-t) p_1 p_2 + (t^2 - t) p_2^2{}\]
\[{}= (1-t) p_1^2 + t p_2^2{}\]
\[{}- t(1-t) (p_1 - p_2)^2.{}\]
Since \(t \in [0,1]\), \(t (1-t) (p_1-p_2) \geq 0\) and consequently
\[ ((1-t) p_1 + t p_2)^2 \leq (1-t) p_1^2 + t p_2^2 \]
whenever \(p_1,p_2 \in {\mathbb R}\) and \(t \in [0,1]\).
2. Convexity Implies Continuity
Claim
If \(f\) is convex on the interval \(I\), if \(p_1,p_2 \in I\), and \(t \not \in [0,1]\), then whenever \((1-t) p_1 + t p_2 \in I\), it must be the case that
\[{}(1-t) f(p_1) + t f(p_2){}\]
\[{}\leq f((1-t)p_1 + t p_2).{}\]
In other words, for \(t\) outside \([0,1]\), the direction of the convexity inequality is reversed whenever all the parts are defined.
Proof
Suppose \(p_3 = (1-t) p_1 + t p_2\) for some point \(p_3 \in I\), assuming that \(p_1,p_2 \in I\) as well. If it were the case that
\[ (1-t) f(p_1) + t f(p_2) > f(p_3) \]
we can demonstrate a contradiction as follows. The illustration below suggests the method of proof in one of two basic cases. Roughly speaking, if the graph of \(f\) at \(x = p_3\) lies below the secant line joining \((p_1,f(p_1))\) and \((p_2,f(p_2))\) (the blue line in the picture), then we can use convexity a second time (the purple line) to show that the value of \(f\) at either \(p_1\) or \(p_2\) would have to be smaller than it actually is (in the picture, the purple line passes below the graph at \(x = p_2\), which would mean by convexity that \(f(p_2) < f(p_2)\).)
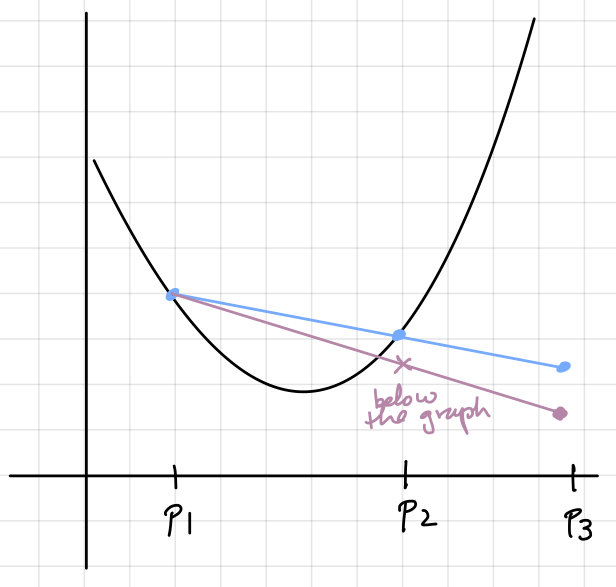
Since \(p_3 = (1-t) p_1 + t p_2\), we can write
- \(p_2 = (1 - t^{-1}) p_1 + t^{-1} p_3\) if \(t > 1\) and
- \(p_1 = -t (1-t)^{-1} p_2 + (1-t)^{-1} p_3\) if \(t < 0\). In this latter case, note that \(-t (1-t)^{-1} = 1 - (1-t)^{-1}\).
So we have
- \(p_2 = (1-u) p_1 + u p_3\) when \(t > 1\) with \(u := t^{-1} \in (0,1]\) and
- \(p_1 = (1-v) p_2 + v p_3\) when \(t < 0\) with \(v := (1-t)^{-1} \in (0,1]\).
By convexity of \(f\), it follows
- \(f(p_2) \leq (1-u) f(p_1) + u f(p_3)\) when \(t > 1\) and
- \(f(p_1) \leq (1-v) f(p_2) + v f(p_3)\) when \(t < 0\).
In each case, we have assumed that it is possible to bound \(f(p_3)\) above by \((1-t) f(p_1) + t f(p_2)\). Using that inequality gives
- \(f(p_2) < (1-u) f(p_1) + u ( (1-t) f(p_1) + t f(p_2))\) when \(t > 1\) and
- \(f(p_1) < (1-v) f(p_2) + v ( (1-t) f(p_1) + t f(p_2))\) when \(t < 0\).
Now simplify each inequality. In the former case,
\[{}1 - u + u(1-t){}\]
\[{}= 1 - t^{-1} + t^{-1}(1-t) = 0{}\]
and \(u t = 1\), so the inequality simplifies to the clearly nonsensical statement that \(f(p_2) < f(p_2)\) when \(t > 1\). Similarly, when \(t < 0\), the inequality just derived reduces to \(f(p_1) < f(p_1)\).
Theorem
Every convex function \(f\) on the interval \(I\) is continuous on the interior of \(I\).
Proof
Let \(x_0\) belong to the interior of \(I\) and let \(a\) and \(b\) be points in \(I\) which are less than \(x_0\) and greater than \(x_0\) respectively. By the above claim and convexity, it follows that
- On the interval \([x_0,b]\), the function \(f(x)\) lies above the line passing through \((a,f(a))\) and \((x_0,f(x_0))\) and below the line passing through \(f(x_0,f(x_0))\) and \((b,f(b))\).
- On the interval \([a,x_0]\), the function \(f(x)\) lies below the line passing through \((a,f(a))\) and \((x_0,f(x_0))\) and above the line passing through \(f(x_0,f(x_0))\) and \((b,f(b))\).
Thus continuity at \(x_0\) follows by the Squeeze Theorem. More precisely, since both lines above are graphs of continuous functions and pass through \((x_0,f(x_0))\), there is some \(\delta\) such that when \(|x-x_0| < \delta\), each line has a height \(y\) which differs from \(f(x_0)\) by at most \(\epsilon\). Since the graph of \(f(x)\) lies between the two lines, \(|f(x) - f(x_0)| < \epsilon\) as well for each such \(x\) (provided that we take \(\delta\) so small that \(\delta < \min\{ |x_0 - a|, |b - x_0|\}\) as well so that the interval \([x_0-\delta,x_0+\delta]\) is contained in \([a,b]\)).
3. Convexity and Differentiability
Claim
Suppose \(f\) is convex on the interval \(I\) and that \(p < q\) are points in \(I\). Then the difference quotient
\[ \frac{f(q) - f(p)}{q-p}\]
is nondecreasing as a function of both \(p\) and \(q\) separately. In other words, if \(p\) is fixed, the difference quotient is nondecreasing as a function of \(q\) on \(I \cap (p,\infty)\) and if \(q\) is fixed, the difference quotient is nondecreasing as a function of \(p\) on \(I \cap (-\infty,q)\).
Proof
Suppose \(p < q_1 < q_2\) are points in \(I\). We can write
\[ q_2 = \left(1 - \frac{q_2 - p}{q_1 - p} \right) p + \frac{q_2 - p}{q_1 - p} q_1 \]
and that \(t := (q_2 - p)/(q_1-p)\) is strictly greater than \(1\). It follows by the previous claim that
\[ (1-t) f(p) + t f(q_1) \leq f(q_2). \]
Subtracting an \(f(p)\) from both sides and substituting in the definition of \(t\) gives that
\[ \frac{q_2 - p}{q_1 - p} (f(q_1) - f(p)) \leq f(q_2) - f(p), \]
and dividing both sides by the positive quantity \(q_2-p\) gives that the difference quotient between \(q_1\) and \(p\) is dominated by the difference quotient between \(q_2\) and \(p\).
If instead we have \(p_1 < p_2 < q\), we instead write
\[ p_1 = \left(1 - \frac{p_1 - p_2}{q-p_2} \right) p_2 + \frac{p_1 - p_2}{q-p_2} q, \]
note that \(t := (p_1 - p_2)/(q-p_2) < 0\), and use the previous claim to see that
\[ (1-t) f(p_2) + t f(q) \leq f(p_1). \]
Negating the inequality and adding \(f(q)\) to both sides gives
\[ (1-t) (f(q) - f(p_2)) \geq f(q) - f(p_1). \]
Now \(1-t = (q-p_1)/(q-p_2)\), so dividing both sides by the positive quantity \(q - p_1\) gives the desired inequality.
Theorem
Suppose that \(f\) is differentiable on some open interval \(I\). Then \(f\) is convex if and only if \(f'\) is a nondecreasing function.
Proof
\([\Rightarrow]\) Fix points \(a<b \in I\). We know that
\[{}\frac{f(b)-f(t)}{b-t}{}\]
is an increasing function of \(t\) when \(t < b\). So comparing the value at \(t = a\) with the limit as \(t \rightarrow b^{-}\) gives that
\[{}\frac{f(b) - f(a)}{b-a}{}\]
\[{}\leq \lim_{t \rightarrow b^{-}} \frac{f(b)-f(t)}{b-t}{}\]
\[{}= f'(b).{}\]
Likewise since \((f(t) - f(a))/(t-a)\) increases when \(t > a\), we have that
\[{}\frac{f(b) - f(a)}{b-a}{}\]
\[{}\geq \lim_{t \rightarrow a^{+}} \frac{f(t)-f(a)}{t-a}{}\]
\[{}= f'(a).{}\]
Combining these inequalities gives \(f'(a) \leq f'(b)\).
\([\Leftarrow]\) Suppose that \(f'\) is nondecreasing. Fix \(a,b \in I\) and \(t \in [0,1]\). Let \(c := (1-t) a + t b\). Without loss of generality, we may assume that \(a < b\). Since \(c-a = t(b-a) \leq b-a\) and since \(t\) and \(b-a\) are positive, it's easy to see that \(c\) lies between \(a\) and \(b\). If \(t = 0,1\) (so \(c = a\) or \(c=b\)), the inequality we need to prove is trivially an equality. So we may assume \(t \in (0,1)\) and that \(c\) is strictly between \(a\) and \(b\). So the Mean Value Theorem says that
\[ \frac{f(c) - f(a)}{c-a} = f'(\xi_1) \]
and
\[ \frac{f(b) - f(c)}{b-c} = f'(\xi_2) \]
for some points \(\xi_1, \xi_2\) satisfying \(a < \xi_1 < c < \xi_2 < b\). Monotonicity of the derivatives implies that \(f'(\xi_1) \leq f'(\xi_2)\), so
\[ \frac{f(c) - f(a)}{c-a} \leq \frac{f(b) - f(c)}{b-c}. \]
Moving \(f(c)\) terms to the left-hand side and all others to the right gives
\[{}f(c) \left[ \frac{1}{c-a} + \frac{1}{b-c} \right]{}\]
\[{}\leq \frac{f(a)}{c-a} + \frac{f(b)}{b-c}. {}\]
Since \(c-a\) and \(b-c\) are positive, we can multiply both sides by the positive quantity \((c-a)(b-c)/(b-a)\) and obtain
\[ f(c) \leq \frac{b-c}{b-a} f(a) + \frac{c-a}{b-a} f(b). \]
This is exactly the desired inequality because \(c-a = t (b-a)\) and \((b-c)/(b-a) = 1 - t\).
Corollary
If \(f\) is a twice-differentiable function on an open interval \(I\), then \(f\) is convex if and only if \(f'' \geq 0\) on \(I\).
Proof
\([\Leftarrow]\) if \(f'' \geq 0\), then we have already seen (via the Mean Value Theorem) that \(f'\) must be increasing, and therefore \(f\) must be convex.
\([\Rightarrow]\) If \(f''(t_0) < 0\) for some \(t_0 \in I\), then for all \(a \neq t_0\) sufficiently close to \(t_0\), the difference quotient \(\frac{f'(a) - f'(t_0)}{a - t_0}\) must be strictly negative. But taking \(a\) to be any such number close to but larger than \(t_0\) would imply that \(f'(a) < f'(t_0)\), contradicting the monotonicity of \(f'\).
Important
Bear in mind that convex functions don't necessarily have to be differentiable at any particular point. An example is the absolute value function. It's not differentiable at \(x = 0\), but
\[{}|(1-t) a + t b|{}\]
\[{}\leq |1-t||a| + |t| |b|{}\]
\[{}= (1-t)|a| + t |b|{}\]
by the triangle inequality (and using the fact that \(t \in [0,1]\)). But if we are working with specific functions already known to be once or twice differentiable, we can use the conditions above (namely, that \(f'\) is nondecreasing for once-differentiable functions and that \(f'' \geq 0\) for twice-differentiable functions) to conclusively determine whether or not they are convex. The point is that in these cases, we have easy ways to check whether convexity holds, and when it does, we are allowed to use convexity to deduce nontrivial inequalities which can be useful.