The Intermediate Value Theorem
1. Images of Connected Domains
Theorem
Suppose that \(E \subset {\mathbb R}\) and let \(f \ : \ E \rightarrow {\mathbb R}\) be continuous. If \(E\) is connected, then \(f(E)\) is also connected.
Proof
Suppose \(f(E)\) is disconnected. There must exist open sets \(A\) and \(B\) such that \(f(E) \cap A\) and \(f(E) \cap B\) are disjoint, nonempty, and have union \(f(E)\). But
\[{}f^{-1}(f(E) \cap A){}\]
\[{}= f^{-1}(f(E)) \cap f^{-1}(A){}\]
\[{}= E \cap f^{-1}(A){}\]
and
\[{}f^{-1}(f(E) \cap B) = E \cap f^{-1}(B).{}\]
Because \(f\) is continuous and \(A\) and \(B\) are open, both \(f^{-1}(A)\) and \(f^{-1}(B)\) are relatively open in \(E\), i.e., there exist open sets \(U\) and \(V\) such that \(f^{-1}(A) = U \cap E\) and \(f^{-1}(B) = V \cap E\). It follows that \(f^{-1}(f(E) \cap A) = E \cap U\) and \(f^{-1}(f(E) \cap B) = E \cap V\).
Now the sets \(E \cap U\) and \(E \cap V\) are:
- Both nonempty: For example, \(f(E) \cap A\) is nonempty and therefore there must be some \(p \in E\) such that \(f(p) \in A\), meaning \(p \in f^{-1}(A) f^{-1} (f(E) \cap A)= E \cap U\).
- Disjoint: \(E \cap U\) and \(E \cap V\) are disjoint, since having a point \(q\) in common would mean that \(q \in f^{-1}(f(E) \cap A)\) and \(q \in f^{-1}(f(E) \cap B)\), giving \(f(q) \in f(E) \cap A\) and \(f(q) \in f(E) \cap B\).
- Have union equal to \(E\): the union of \(f^{-1}(f(E) \cap A)\) and \(f^{-1}(f(E) \cap B)\) must be all of \(f^{-1}(f(E)) = E\), simply because \((f(E) \cap A) \cup (f(E) \cap B) = f(E)\) by assumption. Here \(f^{-1}(f(E)) = E\) because \(f^{-1}\) maps into \(E\) by definition and every \(p \in E\) satisfies \(f(p) \in f(E)\), meaning \(p \in f^{-1} (f(E))\). Thus disconnectedness of \(f(E)\) would imply disconnectedness of \(E\) itself.
Corollary (Intermediate Value Theorem)
Suppose \(I \subset {\mathbb R}\) is an interval and \(f \ : \ I \rightarrow {\mathbb R}\) is continuous. Then for any distinct points \(a,b \in I\), if \(f(a) \neq f(b)\), then for any \(y\) which is between \(f(a)\) and \(f(b)\), there is some point \(x\) between \(a\) and \(b\) such that \(f(x) = y\).
Proof
Without loss of generality, it may be assumed that \(a < b\) and \(f(a) \neq f(b)\). Restricting \(f\) to the interval \([a,b]\), \(f\) remains continuous on \([a,b]\), and certainly \([a,b]\) is a connected set. Thus \(f([a,b])\) is also connected. Since \(f(a)\) and \(f(b)\) are distinct points in the connected set \(f([a,b])\), all points strictly between \(f(a)\) and \(f(b)\) belong to \(f([a,b])\) as well. This means that every \(y\) between \(f(a)\) and \(f(b)\) has \(y \in f([a,b])\), giving that there must be some \(x \in [a,b]\) such that \(f(x) =y\). Since \(y \neq f(a), f(b)\), \(x \neq a,b\) and consequenty \(x \in (a,b)\).
2. Continuity and the Method of Bisection
When \(f\) is continuous on \([a,b]\), we can think of the Intermediate Value Theorem as guaranteeing the existence of a solution \(x\) of the equation \(f(x) = y\) whenever \(y\) is strictly between \(f(a)\) and \(f(b)\). This suggests an alternate proof which is somewhat more constructive than the version presented above which is instead based on the Method of Bisection.
Recall the schematic picture which was used to illustrate the Method of Bisection in the special case of solving the equation \(x^k - A = 0\):
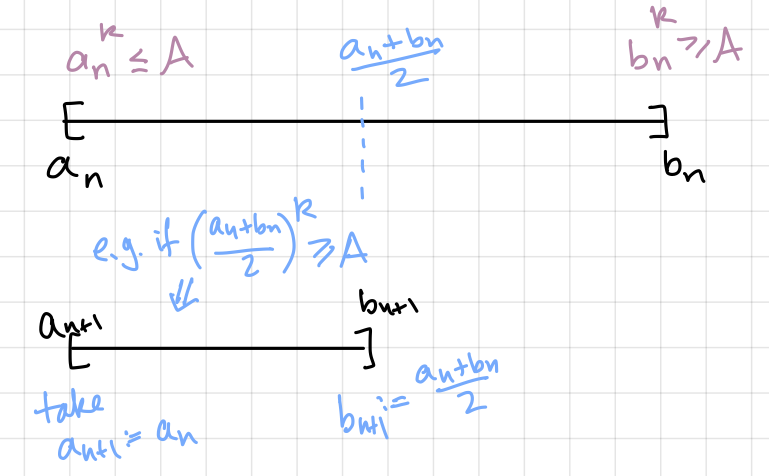
In the general case, suppose that \(f(a) \neq f(b)\) and \(y\) is strictly between \(f(a)\) and \(f(b)\). Suppose for simplicity that \(f(a) < y < f(b)\) (the remaining case \(f(b) < y < f(a)\) can be treated simply by reversing the roles of greater than and less than in the argument that follows). Let \(a_0 := a\), \(b_0 := b\). Suppose that for some fixed \(n\), \(a_0,\ldots, a_n\) and \(b_0,\ldots,b_n\) have been defined so that \(a_0 \leq a_1 \leq \cdots a_k \leq b_k \leq \cdots \leq b_1 \leq b_0\) and that \(f(a_i) \leq y \leq f(b_i)\) for each \(i = 0,\ldots,n\). Suppose also that \(|b_i - a_i| = 2^{-i} |b-a|\) for each \(i = 0,\ldots,n\). Let \(z_{n+1} := \frac{a_n+b_n}{2}\). If \(f(z_{n+1}) < y\), let \(a_{n+1} := z_{n+1}\) and \(b_{n+1} := b_n\). Otherwise let \(a_{n+1} := a_n\) and \(b_{n+1} := z_{n+1}\). It follows that we have inductively defined infinite sequences \(\{a_n\}_{n=1}^\infty\) and \(\{b_n\}_{n=1}^\infty\) such that \(f(a_n) \leq y\) for all \(n\) and \(f(b_n) \geq y\) for all \(n\). These sequences also have \(|a_n - b_n| = 2^{-n}|b-a|\) for each \(n\). Since the sequences are bounded and monotone, both sequences converge, and since \(b_n - a_n \rightarrow 0\) as \(n \rightarrow \infty\), they both converge to the same point \(x\). Then \(f(x) = \lim_{n \rightarrow \infty} f(a_n) \leq y\) and \(f(x) = \lim_{n \rightarrow \infty} f(b_n) \geq y\), so \(f(x) = y\).
Notice that this proof is essentially a repackaging of several arguments that we have used at various points when proving results about continuity and connectedness.
Exercise
Suppose the Method of Bisection is used to solve the equation \(x^2 = 3\) on the interval \([-1,2]\). Verify that, in fact, the method does yield a solution. Is the solution yielded by this method equal to \(-\sqrt{3}\) or \(\sqrt{3}\)?