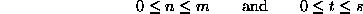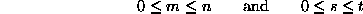Math 480 Course Notes -- June 4, 1996
Examples of Stochastic processes continuous in time, discrete in space
The simplest useful example of a stochastic process that is continuous in time but discrete in space is the Poisson process. The Poisson process is a special case of a set of processes called birth processes. In these processes, the sample space for each random variable X(t) is the set of non-negative integers, and for each non-negative integer x, we choose a positive real parameter 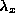 which will be equal to both
which will be equal to both 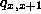 and
and 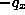 . Thus, in such a process, the value of X can either jump up by 1 or stay the same. The time until the process jumps up by one, starting from X=x, is exponentially distrubuited with parameter
. Thus, in such a process, the value of X can either jump up by 1 or stay the same. The time until the process jumps up by one, starting from X=x, is exponentially distrubuited with parameter 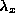 . So if we think of X as representing a population, it is one that experiences only births (one at a time) at random times, but no deaths.
. So if we think of X as representing a population, it is one that experiences only births (one at a time) at random times, but no deaths.
The specialization in the Poisson process is that 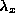 is chosen to have the same value,
is chosen to have the same value, 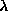 , for all x. Since we move one step to the right (on the x-axis) according to the exponential distribution, we can conclude without much thought that
, for all x. Since we move one step to the right (on the x-axis) according to the exponential distribution, we can conclude without much thought that
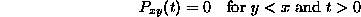
and that

for all t>0. To learn any more, we must consider the system of differential equations (the "forward equations") derived in the preceding lecture.
Recall that the forward equation
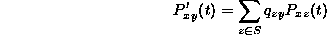
gave the rate of change in the probability of being at y (given that the process started at x) in terms of the probabilities of jumping to y from any z just at time t (the terms of the sum for 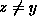 ) and (minus) the probability of already being at y and jumping away just at time t (recall that
) and (minus) the probability of already being at y and jumping away just at time t (recall that 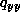 is neagtive.
is neagtive.
For the Poisson process, the forward equations simplify considerably, because 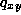 is nonzero only if x=y or if y=x+1. And for these values we have:
is nonzero only if x=y or if y=x+1. And for these values we have:
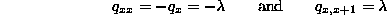
Therefore the forward equation reduces to:
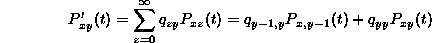
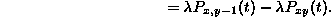
We interpret this equation as saying that 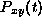 changes by increasing due to births from state y-1, and decreases due to births starting from state y. Since we already know
changes by increasing due to births from state y-1, and decreases due to births starting from state y. Since we already know 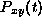 for
for 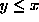 , we will use the preceding differential equation inductively to calculate
, we will use the preceding differential equation inductively to calculate 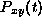 for y> x, one y at a time.
for y> x, one y at a time.
To do this, though, we need the fact that the solution of the linear first-order differential equation

is
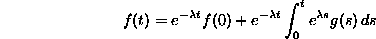
Click here for the details of the derivation of this formula.
Using this formula for the solution of the differential equation, we substitute 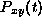 for f(t), and
for f(t), and 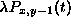 for g(t). We get that
for g(t). We get that
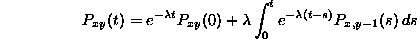
Since we are assuming that the process starts at x, i.e., X(0)=x, we know that 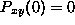 for all
for all 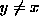 and
and 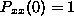 . In other words
. In other words

(this is the Kronecker delta).
Now we are ready to compute. Note that we have to compute 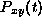 for all possible nonnegative integer values of x and y. In other words, we have to fill in all the entries in the table:
for all possible nonnegative integer values of x and y. In other words, we have to fill in all the entries in the table:
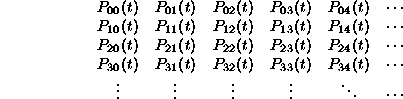
Of course, we already know part of the table:
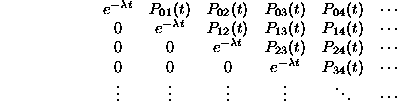
So we begin the induction:
We know that

so we can use the differential equation
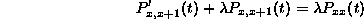
to get that
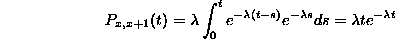
Note that this fills in the next diagonal of the table.
Then we can use the differential equation
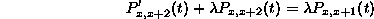
to get that
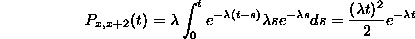
Continuing by induction (exercise 1 below!) we get that
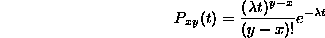
provided 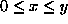 and t>0. This means that the random variable X(t) (this is the infinite discrete random variable that gives the value of x at time t, i.e., tells how many jumps have happened up until time t), has a Poisson distribution with parameter
and t>0. This means that the random variable X(t) (this is the infinite discrete random variable that gives the value of x at time t, i.e., tells how many jumps have happened up until time t), has a Poisson distribution with parameter 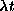 This is the important connection between the exponential distribution and the Poisson distribution.
This is the important connection between the exponential distribution and the Poisson distribution.
Homework
1. Do the induction proof -- show that
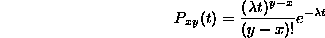
provided 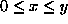 and t> 0 given the work above.
and t> 0 given the work above.
2. Draw some graphs of the distribution of X(t) for various values of t (and 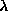 ). What happens as t increases?
). What happens as t increases?
3. Since 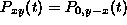 for all positive t, show that if X(0)=x, then the random variable X(t)-x has a Poisson distribution with parameter
for all positive t, show that if X(0)=x, then the random variable X(t)-x has a Poisson distribution with parameter 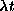 . Then, use the Markov assumption to prove that X(t)-X(s) has Poisson distribution with parameter
. Then, use the Markov assumption to prove that X(t)-X(s) has Poisson distribution with parameter 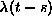 .
.
4. Let 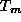 be the continuous random variable that gives the time to the mth jump of a Poisson process with parameter
be the continuous random variable that gives the time to the mth jump of a Poisson process with parameter 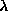 . Find the pdf of
. Find the pdf of 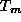 .
.
5. For a Poisson process with parameter 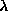 , find
, find 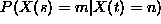 , both for the case
, both for the case
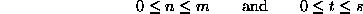
and the case
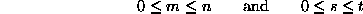
Dennis DeTurck
Fri Jun 7 16:34:24 EDT 1996
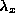 which will be equal to both
which will be equal to both 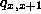 and
and 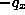 . Thus, in such a process, the value of X can either jump up by 1 or stay the same. The time until the process jumps up by one, starting from X=x, is exponentially distrubuited with parameter
. Thus, in such a process, the value of X can either jump up by 1 or stay the same. The time until the process jumps up by one, starting from X=x, is exponentially distrubuited with parameter 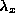 . So if we think of X as representing a population, it is one that experiences only births (one at a time) at random times, but no deaths.
. So if we think of X as representing a population, it is one that experiences only births (one at a time) at random times, but no deaths.
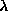 , for all x. Since we move one step to the right (on the x-axis) according to the exponential distribution, we can conclude without much thought that
, for all x. Since we move one step to the right (on the x-axis) according to the exponential distribution, we can conclude without much thought that 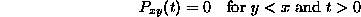

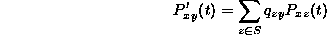
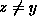 ) and (minus) the probability of already being at y and jumping away just at time t (recall that
) and (minus) the probability of already being at y and jumping away just at time t (recall that 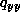 is neagtive.
is neagtive.
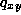 is nonzero only if x=y or if y=x+1. And for these values we have:
is nonzero only if x=y or if y=x+1. And for these values we have:
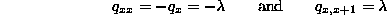
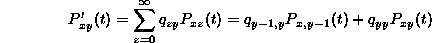
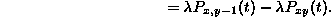
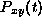 changes by increasing due to births from state y-1, and decreases due to births starting from state y. Since we already know
changes by increasing due to births from state y-1, and decreases due to births starting from state y. Since we already know 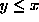 , we will use the preceding differential equation inductively to calculate
, we will use the preceding differential equation inductively to calculate 
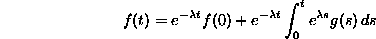
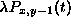 for g(t). We get that
for g(t). We get that
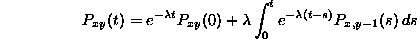
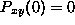 for all
for all 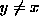 and
and 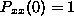 . In other words
. In other words 
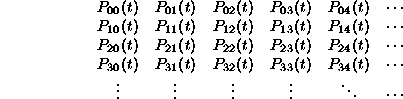
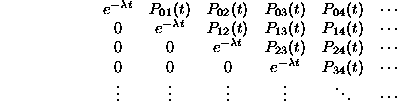
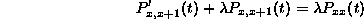
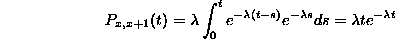
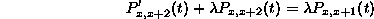
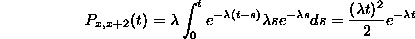
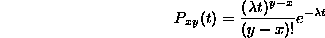
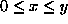 and t>0. This means that the random variable X(t) (this is the infinite discrete random variable that gives the value of x at time t, i.e., tells how many jumps have happened up until time t), has a Poisson distribution with parameter
and t>0. This means that the random variable X(t) (this is the infinite discrete random variable that gives the value of x at time t, i.e., tells how many jumps have happened up until time t), has a Poisson distribution with parameter 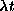 This is the important connection between the exponential distribution and the Poisson distribution.
This is the important connection between the exponential distribution and the Poisson distribution.
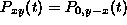 for all positive t, show that if X(0)=x, then the random variable X(t)-x has a Poisson distribution with parameter
for all positive t, show that if X(0)=x, then the random variable X(t)-x has a Poisson distribution with parameter 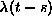 .
.
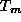 be the continuous random variable that gives the time to the mth jump of a Poisson process with parameter
be the continuous random variable that gives the time to the mth jump of a Poisson process with parameter 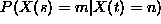 , both for the case
, both for the case