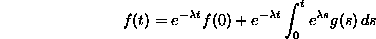Consider the linear differential equation of the form

where f and g are functions of t and 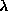 is a constant. We assume that g(t) is given and we wish to find f(t).
is a constant. We assume that g(t) is given and we wish to find f(t).
To solve such equations, we make the left side have the form of the derivative of a product by multiplying through by  :
:

We recognize the left as the derivative of the product of  and f:
and f:

We can integrate both sides of this (with s substituted for t) from 0 to t to recover f(t):

Of course, the integral of the derivative on the left side of the equation may be evaluated using the (second) fundamental theorem of calculus:

Now we can solve algebraically for f(t):