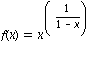Limits and Continuity (Thomas-Finney Section 1.1, page 59, Problem 19

Examine the limiting behavior of 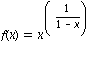   at x=1..

>	f:=x^(1/(1-x));

We start by calculating the value of f(x) for values of x near 1, to see if we can figure out what f(1) should be.

>	for j from 1 to 5 do print(1-(.1)^j, evalf(subs(x=1-(.1)^j,f))) od;

>	for j from 1 to 5 do print(1+.1^j, evalf(subs(x=1+.1^j,f))) od;

It appears that as we approach x=1 from either side, f is approaching a value of around .36788 or so.

>	plot(f,x=0..2,color=blue,thickness=2);

The graph appears to be continuous, and even though the function is not defined at x=1, it seems as though a limit does exist which would make the function continuous.  We can plot over a smaller domain ("zoom") to get a better idea of the limit:

>	plot(f,x=0.8..1.2,color=blue,thickness=2);

It certainly looks like there is a limit. We use Maple to calculate the actual limit:

>	limit(f,x=1);

>

evalf(%);

p. 59, Problem 29

Calculatethe average rate of change of over the intervals (a) [2,3], and (b) [-1,1]..

Thise is easy in Maple:

>	f:=x->x^3+1;

>	aroc1:=(f(3)-f(2))/(3-2);

>	aroc2:=(f(1)-f(-1))/(1-(-1));

Section 1.2, page 65, Problem 17

Calculate as .  Let's just do this one directly:

>	Limit((x-5)/(x^2-25),x=5)=limit((x-5)/(x^2-25),x=5);

Problem 21

Calculate 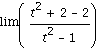as . Let's explore this one a little more carefully:

>	f(t) := (t^2+t-2)/(t^2-1);

Let's start by plotting the function and seeing if anything obvious goes wrong.

>	plot(f(t), t=0..2,color=blue,thickness=2);

The graph looks continuous, so let's see if we can just plug in t=1.

>	subs(t=1,f(t));

Error, numeric exception: division by zero

In fact, note that when we plug in t=1, both the numerator and denominator become zero.  So both polynomials are divisible by (t-1).

>	simplify((t^2+t-2)/(t-1));

>	simplify((t^2-1)/(t-1));

So in fact we can cancel the (t-1) factors and get

>	g(t):=simplify((t^2+t-2)/(t^2-1));

Now when we try to evaluate g(t) we see that we do indeed get an answer, which will be the limit we seek.

>	subs(t=1,g(t));

Note that we could have just directly solved this problem by doing

>	limit(f(t),t=1);

Section 1.3, page 75, Problem 17

Find an open interval in which .

We want to give evidence for the fact that by finding for .

>	f:=x->sqrt(x+1);

>	solve(abs(f(0+delta)-1)<1/10);

So \we will have provided .

Section 1.4, page 85,  Problem 15

Compute 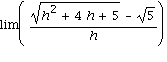as .  

Maple makes short work of this:

>	Limit((sqrt(h^2+4*h+5)-sqrt(5))/h,h=0)=limit((sqrt(h^2+4*h+5)-sqrt(5))/h,h=0);

Problem 17

Compute as from the right.

>	f:=x->(x+3)*abs(x+2)/(x+2);

>	limit(f(x),x=-2);

The limit as itself is undefined, however it is possible for us to compute the left and right handed limits.  

>	limit(f(x),x=-2,left);

>	limit(f(x),x=1,right);

So we can see that the limit failed to exist because the left and right limits were different

Problem 24

Compute as from the right.

>	Limit(1/(x-3),x=3,right)=limit(1/(x-3),x=3,right);

Section 1.5, page 95, Problem 41

Let for while for .  For which value of b is this function continuous?

For the function to be continuous at x=-2, the two pieces must agree there:

>	solve(subs(x=-2,x)=subs(x=-2,b*x^2),b);

So the function is continuous for b=-1/2. We can define and plot it to make sure:

>	f:=piecewise(x<-2,x,x>=-2,-1/2*x^2);

>	plot(f,x=-4..4,color=blue,thickness=2);

Section 1.6, page 102, Problem 7

Find an equation for the  tangent to at the point (1,2).

>	f:=x->2*sqrt(x);

We need to find the tangent line at (1,2) - so first we get the slope:

>	tanslope:=limit((f(1+h)-f(1))/h,h=0);

>	tanline:=2+tanslope*(x-1);

Now we can plot:

>	plot({f(x),tanline},x=-0.1..3,color=blue,thickness=2);

Problem 37  Where does the curve 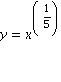have vertical tangents?

>	y:=x^(1/5);

>	plot(y, x=-5..5,color=blue,thickness=2);

It's interesting that we only got the part of the curve for x>0, even though the function exists for x<0 -- to get the whole thing, instead of raising x to the 1/5 power, we'll compute the  5th "surd" (or root) of x:

>	y:=surd(x,5);

>	plot(y,x=-5..5,color=blue,thickness=2);

That's better. It appears that the curve may have a vertical tangent at x=0, but probably does not any other place.  From the definition on p.102, we know that there will be a vertical tangent whenever the following limit is equal to infinity.

>	Limit(((x+h)^(1/5)-x^(1/5))/h,h=0)=limit(((x+h)^(1/5)-x^(1/5))/h,h=0);

This will clearly be infinity if and only if x=0, as we anticipated from the above picture.