Image Gallery
Here's a picture I made of the Finnish snowball, aka the Manhattan cube, or as I prefer, the quasi-Fuchsian box.
 For higher quality, save the enlarged image and use a better image viewer. The picture was made in 2007 using POV-Ray and 23,478 lines of java generated code.
For higher quality, save the enlarged image and use a better image viewer. The picture was made in 2007 using POV-Ray and 23,478 lines of java generated code.
The play an animation I made of the Finnish snowball growing, or better yet, right click to download the video. The video won't play.
This is a picture of the limit set of a certain 3-dimensional hyperbolic reflection group. The quotient is an infinite volume hyperbolic 3-orbifold. The convex core has finite volume and totally geodesic boundary. In my research I study these objects and their geometric deformations.
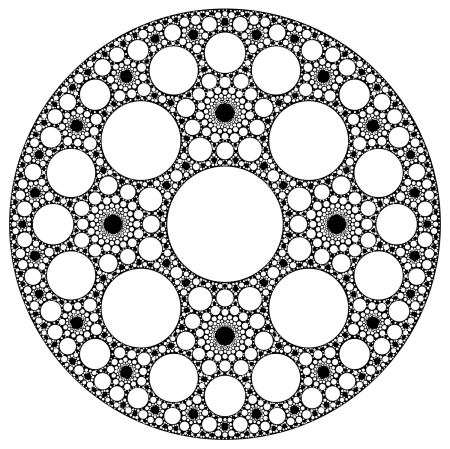 For higher quality, save the enlarged image and use a better image viewer. Note that the black regions of the picture should be filled in with an infinite number of tiny white disks. The picture was made in 2008 using Mathematica.
For higher quality, save the enlarged image and use a better image viewer. Note that the black regions of the picture should be filled in with an infinite number of tiny white disks. The picture was made in 2008 using Mathematica.
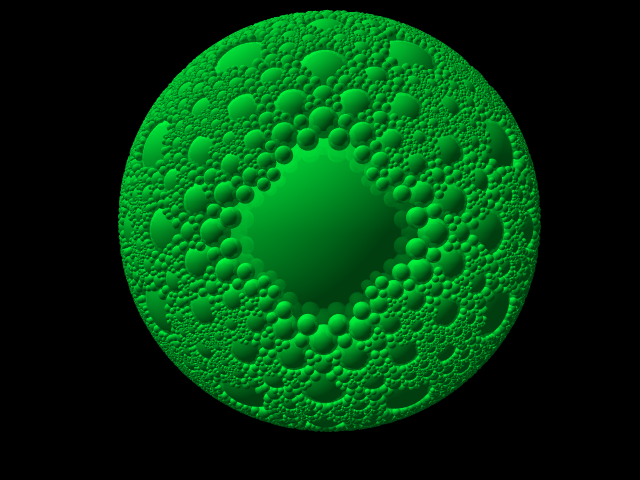
Here's a representation of the limit set of the reflection group studied in my paper with T. Aougab "Infinitesimal rigidity of a compact hyperbolic 4-orbifold with totally geodesic boundary". Briefly, it is built as follows: take the hyperbolic right-angled 120 cell, remove a certain collection of 24 pairwise disjoint (or tangent) walls, and take the reflection group generated by the remaining 96 walls. The quotient is an infinite volume hyperbolic 4-orbifold. The convex core is compact with totally geodesic boundary.

enlarge image (Enlarged image may load very slowly.)
The picture has removed an outermost sphere containing all the others. (With the outermost sphere the picture is not so interesting.) The limit set is the points contained inside the (omitted) outermost sphere but outside all the other spheres. As before, the picture is incomplete. There should be an infinite number of tiny disjoint spheres nearly filling the outermost sphere. The picture was made in 2009 using Sage and POV-Ray.
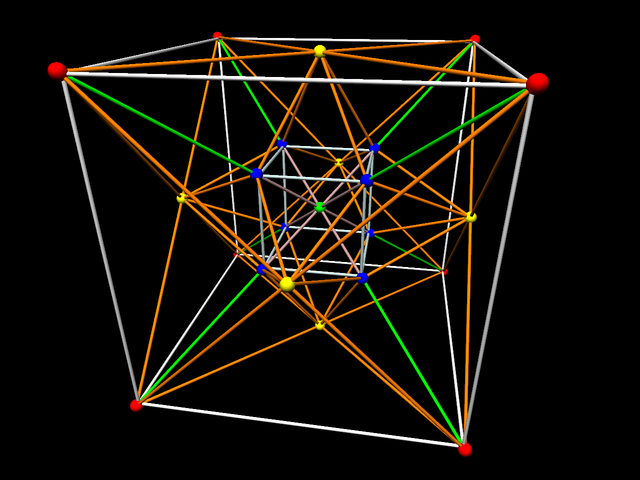
Similarly, here's a representation of the limit set of the reflection group studied in my paper with S. Kerckhoff "From the 24-cell to the cuboctahedron". It is built as follows: take the hyperbolic right-angled 24 cell, remove a certain octet of pairwise disjoint walls, and take the reflection group generated by the remaining 16 walls. The quotient is an infinite volume hyperbolic 4-orbifold. The convex core is finite volume with totally geodesic boundary.
 Again, the picture has removed an outermost sphere containing all the others. The limit set is the points contained inside the (omitted) outermost sphere but outside all the other spheres. As before, the picture is incomplete. There should be an infinite number of tiny tangent spheres nearly filling the outermost sphere. The picture was made in 2009 using Sage and POV-Ray.
Again, the picture has removed an outermost sphere containing all the others. The limit set is the points contained inside the (omitted) outermost sphere but outside all the other spheres. As before, the picture is incomplete. There should be an infinite number of tiny tangent spheres nearly filling the outermost sphere. The picture was made in 2009 using Sage and POV-Ray.
I'm working on putting up some slides taken from the article with Steve Kerckhoff "From the 24-cell to the cuboctahedron". The first installment shows the 2-skeleton of the hyperbolic 24-cell projected into the flat 3-dimensional space at infinity. Go to slideshow. (It uses javascript.)
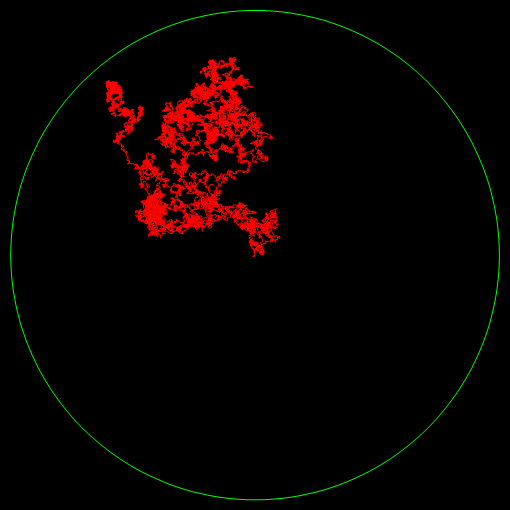
I made some animations showing random walks in the hyperbolic plane. (Again, the animations use javascript.)
Take me back to Pete's homepage.
The computer images on this webpage were made by Peter Storm.






