LU Decomposition Without Pivoting

   

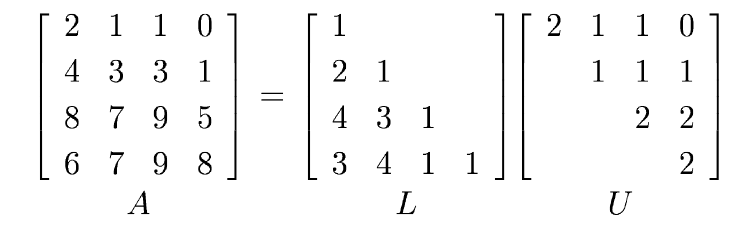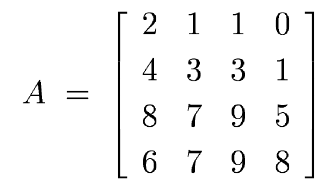
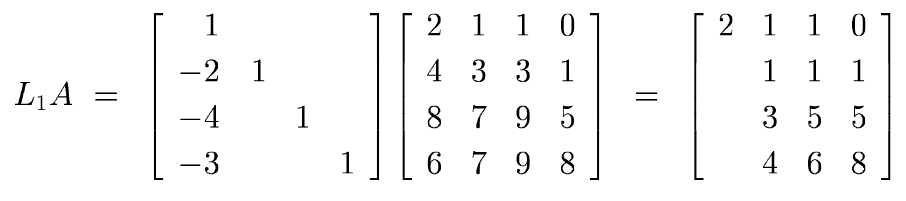
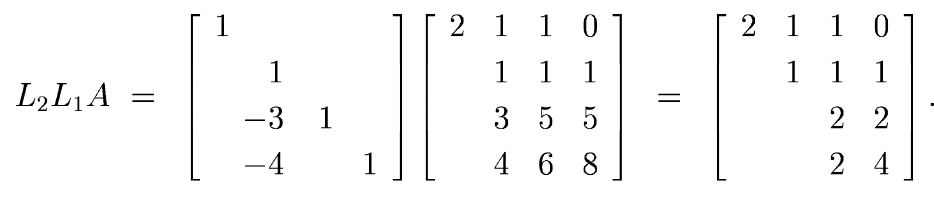
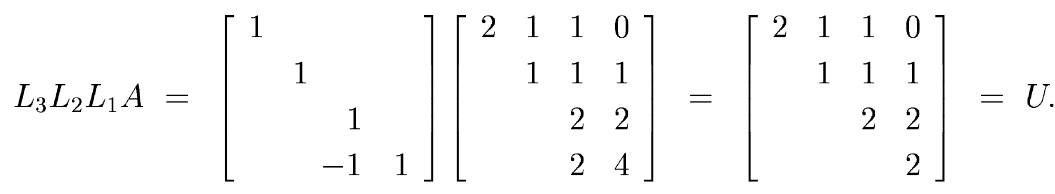
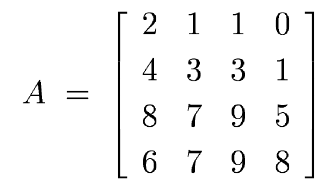
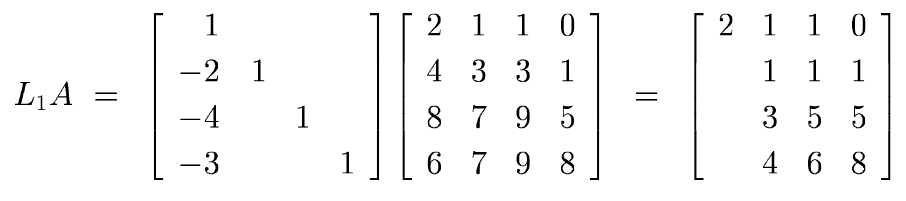
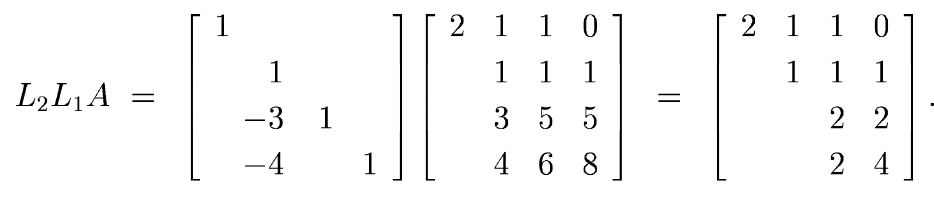
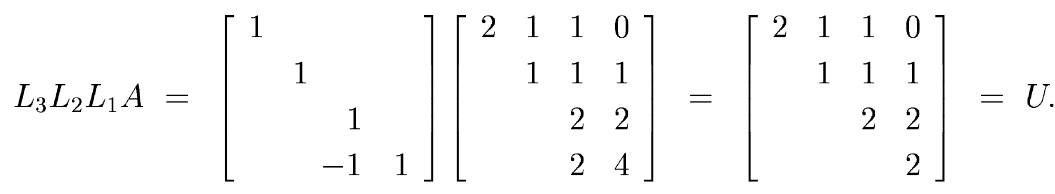
Now, to exhibit the full factorization A = LU, we need to compute the product
L = L₁^-1 L₂^-1 L₃^-1 . Perhaps surprisingly, this turns out to be a triviality. The inverse of L₁ is just L₁ itself, but with each entry below the diagonal negated

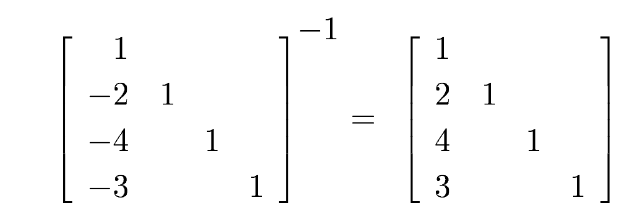
The inverses of L₂ and L₃ are obtained similarly: just negate their sub diagonal entries. Finally, the product   L₁^-1 L₂^-1 L₃^-1   is just the unit lower-triangular matrix with the nonzero sub diagonal entries of L₁^-1, L₂^-1, and L₃^-1 inserted in the appropriate places. Thus