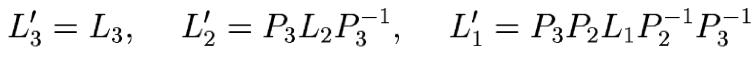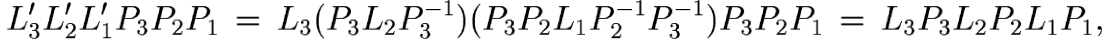LU Decomposition With Pivoting
[Source: Lecture 21 in Trefethen-Bau Numerical Linear Algebra]
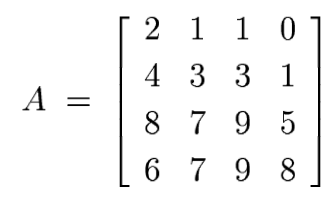
Interchange row 1 and row 3 [left multiplication by P1]:
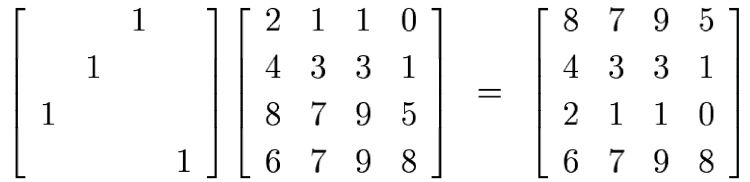
Do elimination on the first column [multiplication by L1]:
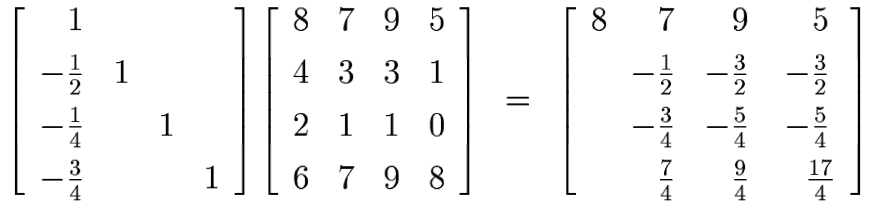
Interchange rows two and four [multiplication by P2]:
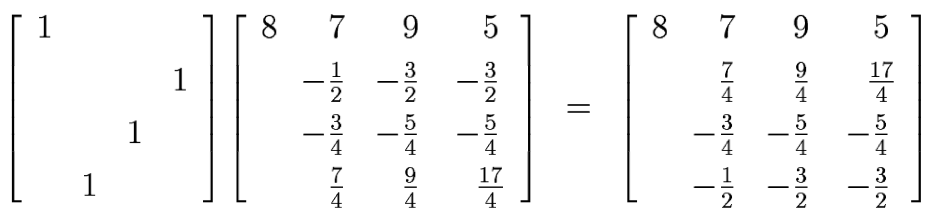
Elimination on the second column [multiplication by L2]:

Interchange rows three and four [multiplication by P3]:
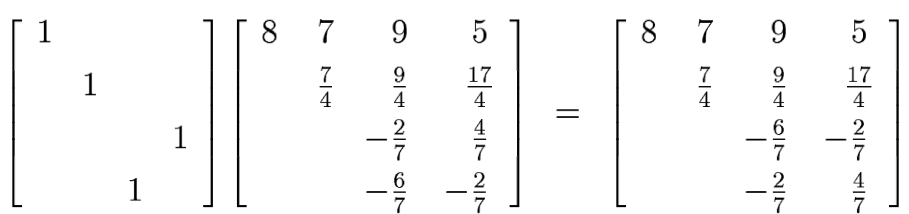
Elimination on the third column [multiplication by L3]:
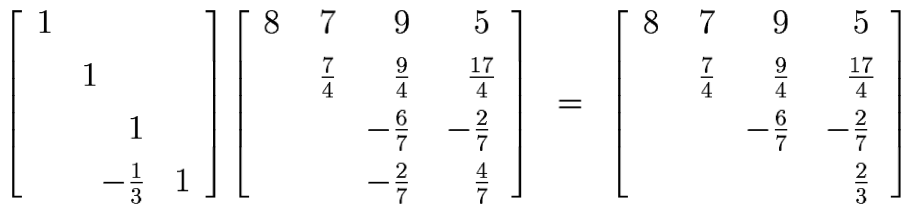
Collecting the pieces we have
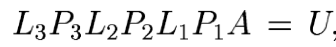
where U is the upper triangular matrix on the right just above --
but the factors to the left of A are not at all lower triangular. We
are lucky there is a fairly simple way out. These six elementary
operations can be reordered in the form
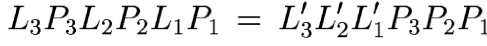 (*)
(*)
where L'k is equal to Lk but with the
subdiagonal entries permuted. To be precise, define
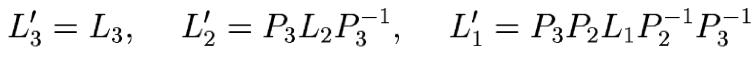
Since each of these definitions apply only permutations
Pj with j>k to Lk, one can verify that
L'k has the same structure as Lk. Computing the
product of the matrices L'k reveals
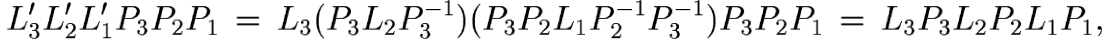
as in equation (*).
The product of the matrices L'k is also unit lower
triangular -- and also easily invertible by negating the subdiagonal
entries., just as in Gaussian elimination without pivoting. Writing
L:=(L'3L'2L'1)-1
and P= P3P2P1,
we have the desired LU factorization of A
PA=LU
This has a pleasant interpretation:
- Permute the rows of A using P.
- Apply Gassian elimination without pivoting to PA.
In theory, this gives insight. But in practice it doesn't help since
we don't know P until the end of the computation.
Note that scaling the rows of A to choose the pivot point does not
change this since the choice of the pivot point is a separate issue.
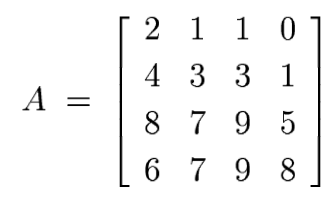
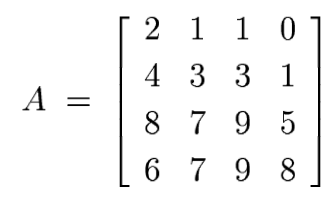
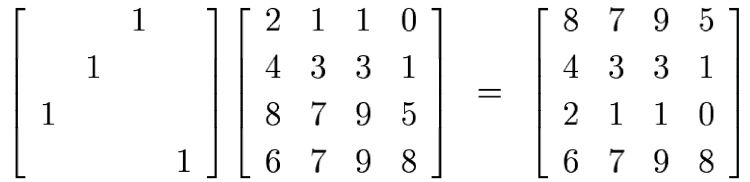
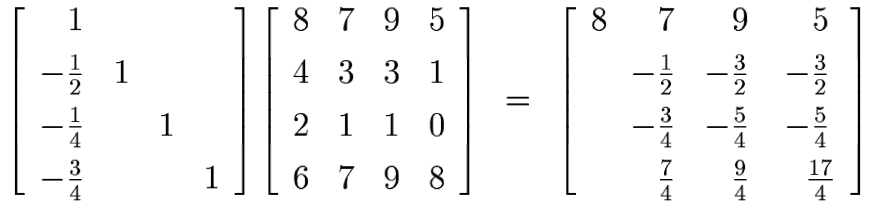
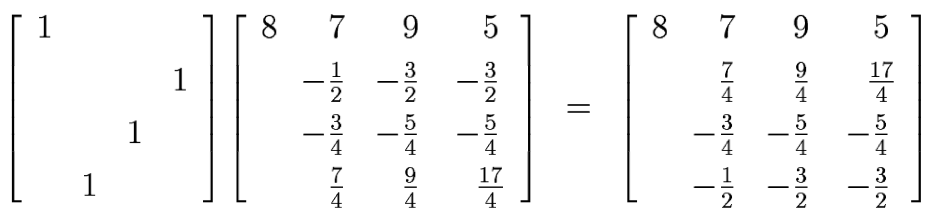
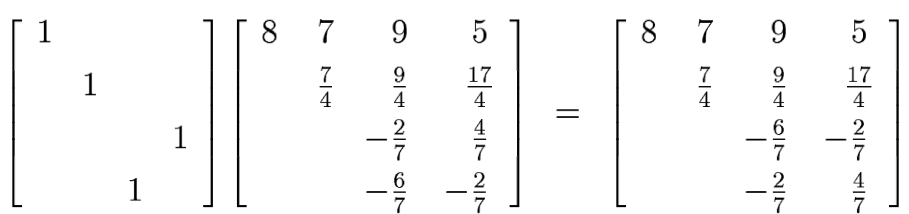
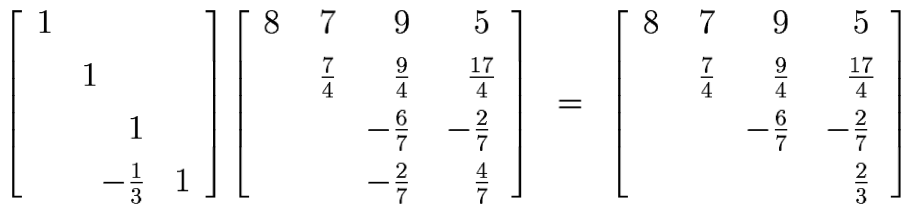
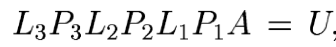
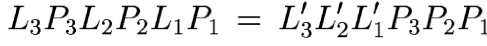 (*)
(*)