RSA (algorithm)
| General | |
|---|---|
| Designers | Ron Rivest, Adi Shamir, and Leonard Adleman |
| First published | 1978 |
| Certification | PKCS#1, ANSI X9.31, IEEE 1363 |
| Cipher detail | |
| Key sizes | 1,024 to 4,096 bit typical |
| Best public cryptanalysis | |
| A 768 bit key has been broken | |
RSA is an algorithm for public-key cryptography that is based on the presumed difficulty of factoring large integers, the factoring problem. RSA stands for Ron Rivest, Adi Shamir and Leonard Adleman, who first publicly described it in 1978. A user of RSA creates and then publishes the product of two large prime numbers, along with an auxiliary value, as their public key. The prime factors must be kept secret. Anyone can use the public key to encrypt a message, but with currently published methods, if the public key is large enough, only someone with knowledge of the prime factors can feasibly decode the message.[1] Whether breaking RSA encryption is as hard as factoring is an open question known as the RSA problem.
Contents |
History
Clifford Cocks, an English mathematician working for the UK intelligence agency GCHQ, described an equivalent system in an internal document in 1973, but given the relatively expensive computers needed to implement it at the time, it was mostly considered a curiosity and, as far as is publicly known, was never deployed. His discovery, however, was not revealed until 1998 due to its top-secret classification, and Rivest, Shamir, and Adleman devised RSA independently of Cocks' work.
The RSA algorithm was publicly described in 1978 by Ron Rivest, Adi Shamir, and Leonard Adleman at MIT; the letters RSA are the initials of their surnames, listed in the same order as on the paper.[2]
MIT was granted U.S. Patent 4,405,829 for a "Cryptographic communications system and method" that used the algorithm in 1983. The patent would have expired on September 21, 2000 (the term of patent was 17 years at the time), but the algorithm was released to the public domain by RSA Security on 6 September 2000, two weeks earlier.[3] Since a paper describing the algorithm had been published in August 1977,[2] prior to the December 1977 filing date of the patent application, regulations in much of the rest of the world precluded patents elsewhere and only the US patent was granted. Had Cocks' work been publicly known, a patent in the US might not have been possible, either.
From the DWPI's abstract of the patent,
The system includes a communications channel coupled to at least one terminal having an encoding device and to at least one terminal having a decoding device. A message-to-be-transferred is enciphered to ciphertext at the encoding terminal by encoding the message as a number M in a predetermined set. That number is then raised to a first predetermined power (associated with the intended receiver) and finally computed. The remainder or residue, C, is... computed when the exponentiated number is divided by the product of two predetermined prime numbers (associated with the intended receiver).
Operation
The RSA algorithm involves three steps: key generation, encryption and decryption.
Key generation
RSA involves a public key and a private key. The public key can be known to everyone and is used for encrypting messages. Messages encrypted with the public key can only be decrypted using the private key. The keys for the RSA algorithm are generated the following way:
- Choose two distinct prime numbers p and q.
- For security purposes, the integers p and q should be chosen at random, and should be of similar bit-length. Prime integers can be efficiently found using a primality test.
- Compute n = pq.
- n is used as the modulus for both the public and private keys
- Compute φ(n) = (p – 1)(q – 1), where φ is Euler's totient function.
- Choose an integer e such that 1 < e < φ(n) and greatest common divisor of (e, φ(n)) = 1; i.e., e and φ(n) are coprime.
- e is released as the public key exponent.
- e having a short bit-length and small Hamming weight results in more efficient encryption - most commonly 0x10001 = 65,537. However, small values of e (such as 3) have been shown to be less secure in some settings.[4]
- Determine d as:
-

- i.e., d is the multiplicative inverse of e mod φ(n).
- This is more clearly stated as solve for d given (de) mod φ(n) = 1
- This is often computed using the extended Euclidean algorithm.
- d is kept as the private key exponent.
The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d which must be kept secret.
Notes:
- An alternative, used by PKCS#1, is to choose d matching de ≡ 1 mod λ with λ = lcm(p − 1, q − 1), where lcm is the least common multiple. Using λ instead of φ(n) allows more choices for d. λ can also be defined using the Carmichael function, λ(n).
- The ANSI X9.31 standard prescribes, IEEE 1363 describes, and PKCS#1 allows, that p and q match additional requirements: be strong primes, and be different enough that Fermat factorization fails.
Encryption
Alice transmits her public key  to Bob and keeps the private key secret. Bob then wishes to send message M to Alice.
to Bob and keeps the private key secret. Bob then wishes to send message M to Alice.
He first turns M into an integer m, such that  by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext
by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext  corresponding to
corresponding to
 .
.
This can be done quickly using the method of exponentiation by squaring. Bob then transmits  to Alice.
to Alice.
Note that at least nine values of m will yield a ciphertext c equal to m,[5] but this is very unlikely to occur in practice.
Decryption
Alice can recover 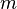 from
from  by using her private key exponent
by using her private key exponent 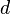 via computing
via computing
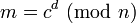 .
.
Given 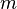 , she can recover the original message M by reversing the padding scheme.
, she can recover the original message M by reversing the padding scheme.
(In practice, there are more efficient methods of calculating  using the pre computed values below.)
using the pre computed values below.)
Using the Chinese remainder algorithm
For efficiency many popular crypto libraries (like OpenSSL, Java and .NET) use the following optimization for decryption and signing: The following values are precomputed and stored as part of the private key:
 and
and  : the primes from the key generation,
: the primes from the key generation,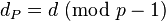 ,
,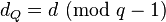 and
and .
.
These values allow the recipient to compute the exponentiation  more efficiently as follows:
more efficiently as follows:
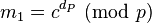
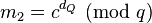
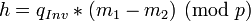 (if
(if 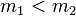 then some libraries compute h as
then some libraries compute h as 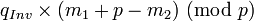 )
)
This is more efficient than computing  even though two modular exponentiations have to be computed. The reason is that these two modular exponentiations both use a smaller exponent and a smaller modulus.
even though two modular exponentiations have to be computed. The reason is that these two modular exponentiations both use a smaller exponent and a smaller modulus.
A working example
Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.
- Choose two distinct prime numbers, such as
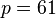 and
and  .
.
- Compute
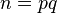 giving
giving
- n = 61 × 53 = 3,233.
- Compute the totient of the product as
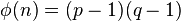 giving
giving
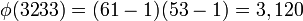 .
.
- Choose any number
 that is coprime to 3,120. Choosing a prime number for
that is coprime to 3,120. Choosing a prime number for  leaves us only to check that
leaves us only to check that  is not a divisor of 3120.
is not a divisor of 3120.
- Let
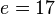 .
.
- Let
- Compute
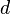 , the modular multiplicative inverse of
, the modular multiplicative inverse of 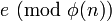 yielding
yielding
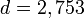 .
.
The public key is ( ,
, 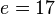 ). For a padded plaintext message
). For a padded plaintext message 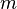 , the encryption function is
, the encryption function is  .
.
The private key is ( ,
, 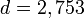 ). For an encrypted ciphertext
). For an encrypted ciphertext  , the decryption function is
, the decryption function is  .
.
For instance, in order to encrypt  , we calculate
, we calculate
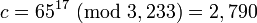 .
.
To decrypt  , we calculate
, we calculate
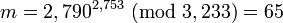 .
.
Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation. In real life situations the primes selected would be much larger; in our example it would be relatively trivial to factor  , 3,233, obtained from the freely available public key back to the primes
, 3,233, obtained from the freely available public key back to the primes  and
and  . Given
. Given  , also from the public key, we could then compute
, also from the public key, we could then compute 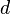 and so acquire the private key.
and so acquire the private key.
Practical implementations use the Chinese remainder theorem to speed up the calculation using modulus of factors (mod pq using mod p and mod q).
The values dp, dq and qInv, which are part of the private key are computed as follows:
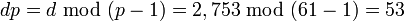
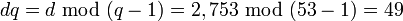
 (Hence:
(Hence:  )
)
Here is how dp, dq and qInv are used for efficient decryption. (Encryption is efficient by choice of public exponent e)
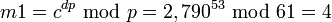

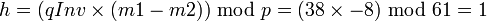
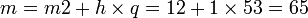 (same as above but computed more efficiently)
(same as above but computed more efficiently)
Attacks against plain RSA
There are a number of attacks against plain RSA as described below.
- When encrypting with low encryption exponents (e.g.,
 ) and small values of the
) and small values of the 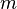 , (i.e.,
, (i.e., 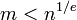 ) the result of
) the result of  is strictly less than the modulus
is strictly less than the modulus  . In this case, ciphertexts can be easily decrypted by taking the
. In this case, ciphertexts can be easily decrypted by taking the  th root of the ciphertext over the integers.
th root of the ciphertext over the integers. - If the same clear text message is sent to
 or more recipients in an encrypted way, and the receivers share the same exponent
or more recipients in an encrypted way, and the receivers share the same exponent  , but different
, but different  ,
,  , and therefore
, and therefore  , then it is easy to decrypt the original clear text message via the Chinese remainder theorem. Johan Håstad noticed that this attack is possible even if the cleartexts are not equal, but the attacker knows a linear relation between them.[6] This attack was later improved by Don Coppersmith.[7]
, then it is easy to decrypt the original clear text message via the Chinese remainder theorem. Johan Håstad noticed that this attack is possible even if the cleartexts are not equal, but the attacker knows a linear relation between them.[6] This attack was later improved by Don Coppersmith.[7]
- Because RSA encryption is a deterministic encryption algorithm (i.e., has no random component) an attacker can successfully launch a chosen plaintext attack against the cryptosystem, by encrypting likely plaintexts under the public key and test if they are equal to the ciphertext. A cryptosystem is called semantically secure if an attacker cannot distinguish two encryptions from each other even if the attacker knows (or has chosen) the corresponding plaintexts. As described above, RSA without padding is not semantically secure.
- RSA has the property that the product of two ciphertexts is equal to the encryption of the product of the respective plaintexts. That is
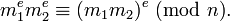 Because of this multiplicative property a chosen-ciphertext attack is possible. E.g., an attacker, who wants to know the decryption of a ciphertext
Because of this multiplicative property a chosen-ciphertext attack is possible. E.g., an attacker, who wants to know the decryption of a ciphertext  may ask the holder of the private key to decrypt an unsuspicious-looking ciphertext
may ask the holder of the private key to decrypt an unsuspicious-looking ciphertext  for some value
for some value  chosen by the attacker. Because of the multiplicative property
chosen by the attacker. Because of the multiplicative property 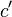 is the encryption of
is the encryption of  . Hence, if the attacker is successful with the attack, he will learn
. Hence, if the attacker is successful with the attack, he will learn  from which he can derive the message m by multiplying
from which he can derive the message m by multiplying  with the modular inverse of
with the modular inverse of  modulo
modulo  .
.
Padding schemes
To avoid these problems, practical RSA implementations typically embed some form of structured, randomized padding into the value 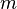 before encrypting it. This padding ensures that
before encrypting it. This padding ensures that 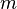 does not fall into the range of insecure plaintexts, and that a given message, once padded, will encrypt to one of a large number of different possible ciphertexts.
does not fall into the range of insecure plaintexts, and that a given message, once padded, will encrypt to one of a large number of different possible ciphertexts.
Standards such as PKCS#1 have been carefully designed to securely pad messages prior to RSA encryption. Because these schemes pad the plaintext 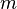 with some number of additional bits, the size of the un-padded message M must be somewhat smaller. RSA padding schemes must be carefully designed so as to prevent sophisticated attacks which may be facilitated by a predictable message structure. Early versions of the PKCS#1 standard (up to version 1.5) used a construction that turned RSA into a semantically secure encryption scheme. This version was later found vulnerable to a practical adaptive chosen ciphertext attack. Later versions of the standard include Optimal Asymmetric Encryption Padding (OAEP), which prevents these attacks. The PKCS#1 standard also incorporates processing schemes designed to provide additional security for RSA signatures (e.g., the Probabilistic Signature Scheme for RSA/RSA-PSS).
with some number of additional bits, the size of the un-padded message M must be somewhat smaller. RSA padding schemes must be carefully designed so as to prevent sophisticated attacks which may be facilitated by a predictable message structure. Early versions of the PKCS#1 standard (up to version 1.5) used a construction that turned RSA into a semantically secure encryption scheme. This version was later found vulnerable to a practical adaptive chosen ciphertext attack. Later versions of the standard include Optimal Asymmetric Encryption Padding (OAEP), which prevents these attacks. The PKCS#1 standard also incorporates processing schemes designed to provide additional security for RSA signatures (e.g., the Probabilistic Signature Scheme for RSA/RSA-PSS).
Signing messages
Suppose Alice uses Bob's public key to send him an encrypted message. In the message, she can claim to be Alice but Bob has no way of verifying that the message was actually from Alice since anyone can use Bob's public key to send him encrypted messages. In order to verify the origin of a message, RSA can also be used to sign a message.
Suppose Alice wishes to send a signed message to Bob. She can use her own private key to do so. She produces a hash value of the message, raises it to the power of  (as she does when decrypting a message), and attaches it as a "signature" to the message. When Bob receives the signed message, he uses the same hash algorithm in conjunction with Alice's public key. He raises the signature to the power of
(as she does when decrypting a message), and attaches it as a "signature" to the message. When Bob receives the signed message, he uses the same hash algorithm in conjunction with Alice's public key. He raises the signature to the power of  (as he does when encrypting a message), and compares the resulting hash value with the message's actual hash value. If the two agree, he knows that the author of the message was in possession of Alice's private key, and that the message has not been tampered with since.
(as he does when encrypting a message), and compares the resulting hash value with the message's actual hash value. If the two agree, he knows that the author of the message was in possession of Alice's private key, and that the message has not been tampered with since.
Secure padding schemes such as RSA-PSS are as essential for the security of message signing as they are for message encryption. (However, patent issues around RSA-PSS mean most people avoid it. Other schemes, perhaps more secure like RSA-OAEP, are available[8]). The same key should never be used for both encryption and signing.[9]
Security and practical considerations
Integer factorization and RSA problem
The security of the RSA cryptosystem is based on two mathematical problems: the problem of factoring large numbers and the RSA problem. Full decryption of an RSA ciphertext is thought to be infeasible on the assumption that both of these problems are hard, i.e., no efficient algorithm exists for solving them. Providing security against partial decryption may require the addition of a secure padding scheme.[citation needed]
The RSA problem is defined as the task of taking  th roots modulo a composite
th roots modulo a composite  : recovering a value
: recovering a value 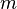 such that
such that  , where
, where  is an RSA public key and
is an RSA public key and  is an RSA ciphertext. Currently the most promising approach to solving the RSA problem is to factor the modulus
is an RSA ciphertext. Currently the most promising approach to solving the RSA problem is to factor the modulus  . With the ability to recover prime factors, an attacker can compute the secret exponent
. With the ability to recover prime factors, an attacker can compute the secret exponent 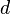 from a public key
from a public key  , then decrypt
, then decrypt  using the standard procedure. To accomplish this, an attacker factors
using the standard procedure. To accomplish this, an attacker factors  into
into  and
and  , and computes
, and computes  which allows the determination of
which allows the determination of 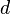 from
from  . No polynomial-time method for factoring large integers on a classical computer has yet been found, but it has not been proven that none exists. See integer factorization for a discussion of this problem. Rivest, Shamir and Adleman note[1] that Miller has shown that - assuming the Extended Riemann Hypothesis (though others call it the Generalized Riemann Hypothesis) - finding d from n and e is as hard as factoring n into p and q (up to a polynomial time difference).[10] However, Rivest, Shamir and Adleman note (in section IX / D of their paper) that they have not found a proof that inverting RSA is equally hard as factoring.
. No polynomial-time method for factoring large integers on a classical computer has yet been found, but it has not been proven that none exists. See integer factorization for a discussion of this problem. Rivest, Shamir and Adleman note[1] that Miller has shown that - assuming the Extended Riemann Hypothesis (though others call it the Generalized Riemann Hypothesis) - finding d from n and e is as hard as factoring n into p and q (up to a polynomial time difference).[10] However, Rivest, Shamir and Adleman note (in section IX / D of their paper) that they have not found a proof that inverting RSA is equally hard as factoring.
As of 2010[update], the largest (known) number factored by a general-purpose factoring algorithm was 768 bits long (see RSA-768), using a state-of-the-art distributed implementation. RSA keys are typically 1024–2048 bits long. Some experts believe that 1024-bit keys may become breakable in the near future (though this is disputed); few see any way that 4096-bit keys could be broken in the foreseeable future. Therefore, it is generally presumed that RSA is secure if  is sufficiently large. If
is sufficiently large. If  is 300 bits or shorter, it can be factored in a few hours on a personal computer, using software already freely available. Keys of 512 bits have been shown to be practically breakable in 1999 when RSA-155 was factored by using several hundred computers and are now factored in a few weeks using common hardware.[11] Exploits using 512-bit code-signing certificates that may have been factored were reported in 2011.[12] A theoretical hardware device named TWIRL and described by Shamir and Tromer in 2003 called into question the security of 1024 bit keys. It is currently recommended that
is 300 bits or shorter, it can be factored in a few hours on a personal computer, using software already freely available. Keys of 512 bits have been shown to be practically breakable in 1999 when RSA-155 was factored by using several hundred computers and are now factored in a few weeks using common hardware.[11] Exploits using 512-bit code-signing certificates that may have been factored were reported in 2011.[12] A theoretical hardware device named TWIRL and described by Shamir and Tromer in 2003 called into question the security of 1024 bit keys. It is currently recommended that  be at least 2048 bits long.[13]
be at least 2048 bits long.[13]
In 1994, Peter Shor showed that a quantum computer (if one could ever be practically created for the purpose) would be able to factor in polynomial time, breaking RSA.
Faulty Key Generation
Finding the large primes p and q is usually done by testing random numbers of the right size with probabilistic primality tests which quickly eliminate virtually all non-primes.
Numbers p and q should not be 'too close', lest the Fermat factorization for n be successful, if p − q, for instance is less than 2n1/4 (which for even small 1024-bit values of n is 3×1077) solving for p and q is trivial. Furthermore, if either p − 1 or q − 1 has only small prime factors, n can be factored quickly by Pollard's p − 1 algorithm, and these values of p or q should therefore be discarded as well.
It is important that the private key d be large enough. Michael J. Wiener showed[14] that if p is between q and 2q (which is quite typical) and d < n1/4/3, then d can be computed efficiently from n and e.
There is no known attack against small public exponents such as e = 3, provided that proper padding is used. However, when no padding is used, or when the padding is improperly implemented, small public exponents have a greater risk of leading to an attack, such as the unpadded plaintext vulnerability listed above. 65537 is a commonly used value for e. This value can be regarded as a compromise between avoiding potential small exponent attacks and still allowing efficient encryptions (or signature verification). The NIST Special Publication on Computer Security (SP 800-78 Rev 1 of August 2007) does not allow public exponents e smaller than 65537, but does not state a reason for this restriction.
Importance of strong random number generation
A cryptographically strong random number generator, which has been properly seeded with adequate entropy, must be used to generate the primes p and q. An analysis comparing millions of public keys gathered from the Internet was recently carried out by Lenstra, Hughes, Augier, Bos, Kleinjung, and Wachter. They were able to factor 0.2% of the keys using only Euclid's algorithm.[15][16] They exploited a weakness unique to cryptosystems based on integer factorization. If n = pq is one public key and n' = p'q' is another, then if by chance p = p', then a simple computation of gcd(n,n' ) = p factors both n and n', totally compromising both keys. Lenstra et al. note that this problem can be minimized by using a strong random seed of bit-length twice the intended security level, or by employing a deterministic function to choose q given p, instead of choosing p and q independently. Nadia Heninger was part of a group that did a similar experiment. They used an idea of Daniel J. Bernstein to compute the GCD of each RSA key n against the product of all the other keys n' they had found (a 729 million digit number), instead of computing each gcd(n,n') separately, thereby achieving a very significant speedup. (After one large division the gcd problem is of normal size.) Heninger says in her blog that the bad keys occurred almost entirely in embedded applications, including "firewalls, routers, VPN devices, remote server administration devices, printers, projectors, and VOIP phones" from over 30 manufactures. Heninger explains that the one-shared-prime problem uncovered by the two groups results from situations where the pseudorandom number generator is poorly seeded initially and then reseeded between the generation of the first and second primes. Using seeds of sufficiently high entropy obtained from key stroke timings or electronic diode noise or atmospheric noise from a radio receiver tuned between stations should solve the problem. [17]
Strong random number generation is important throughout every phase of public key cryptography. For instance, if a weak generator is used for the symmetric keys that are being distributed by RSA, then an eavesdropper could bypass the RSA and guess the symmetric keys directly.
Timing attacks
Kocher described a new attack on RSA in 1995: if the attacker Eve knows Alice's hardware in sufficient detail and is able to measure the decryption times for several known ciphertexts, she can deduce the decryption key 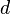 quickly. This attack can also be applied against the RSA signature scheme. In 2003, Boneh and Brumley demonstrated a more practical attack capable of recovering RSA factorizations over a network connection (e.g., from a Secure Socket Layer (SSL)-enabled webserver)[18] This attack takes advantage of information leaked by the Chinese remainder theorem optimization used by many RSA implementations.
quickly. This attack can also be applied against the RSA signature scheme. In 2003, Boneh and Brumley demonstrated a more practical attack capable of recovering RSA factorizations over a network connection (e.g., from a Secure Socket Layer (SSL)-enabled webserver)[18] This attack takes advantage of information leaked by the Chinese remainder theorem optimization used by many RSA implementations.
One way to thwart these attacks is to ensure that the decryption operation takes a constant amount of time for every ciphertext. However, this approach can significantly reduce performance. Instead, most RSA implementations use an alternate technique known as cryptographic blinding. RSA blinding makes use of the multiplicative property of RSA. Instead of computing  , Alice first chooses a secret random value
, Alice first chooses a secret random value  and computes
and computes  . The result of this computation after applying Euler's Theorem is
. The result of this computation after applying Euler's Theorem is  and so the effect of
and so the effect of  can be removed by multiplying by its inverse. A new value of
can be removed by multiplying by its inverse. A new value of  is chosen for each ciphertext. With blinding applied, the decryption time is no longer correlated to the value of the input ciphertext and so the timing attack fails.
is chosen for each ciphertext. With blinding applied, the decryption time is no longer correlated to the value of the input ciphertext and so the timing attack fails.
Adaptive chosen ciphertext attacks
In 1998, Daniel Bleichenbacher described the first practical adaptive chosen ciphertext attack, against RSA-encrypted messages using the PKCS #1 v1 padding scheme (a padding scheme randomizes and adds structure to an RSA-encrypted message, so it is possible to determine whether a decrypted message is valid.) Due to flaws with the PKCS #1 scheme, Bleichenbacher was able to mount a practical attack against RSA implementations of the Secure Socket Layer protocol, and to recover session keys. As a result of this work, cryptographers now recommend the use of provably secure padding schemes such as Optimal Asymmetric Encryption Padding, and RSA Laboratories has released new versions of PKCS #1 that are not vulnerable to these attacks.
Side-channel analysis attacks
A side-channel attack using branch prediction analysis (BPA) has been described. Many processors use a branch predictor to determine whether a conditional branch in the instruction flow of a program is likely to be taken or not. Often these processors also implement simultaneous multithreading (SMT). Branch prediction analysis attacks use a spy process to discover (statistically) the private key when processed with these processors.
Simple Branch Prediction Analysis (SBPA) claims to improve BPA in a non-statistical way. In their paper, "On the Power of Simple Branch Prediction Analysis",[19] the authors of SBPA (Onur Aciicmez and Cetin Kaya Koc) claim to have discovered 508 out of 512 bits of an RSA key in 10 iterations.
A power fault attack on RSA implementations has been described in 2010.[20] The authors recovered the key by varying the CPU power voltage outside limits; this caused multiple power faults on the server.
Proofs of correctness
Proof using Fermat's Little Theorem
The proof of the correctness of RSA is based on Fermat's little theorem. This theorem states that if p is prime and p does not divide an integer a then
We want to show (me)d  m
m  for every integer m when p and q are distinct prime numbers and e and d are positive integers satisfying
for every integer m when p and q are distinct prime numbers and e and d are positive integers satisfying
We can write
for some nonnegative integer h.
To check two numbers, like med and m, are congruent mod pq it suffices (and in fact is equivalent) to check they are congruent mod p and mod q separately. (This is part of the Chinese remainder theorem, although it is not the significant part of that theorem.) To show med  m mod p, we consider two cases: m
m mod p, we consider two cases: m  0 mod p and m
0 mod p and m  0 mod p. In the first case med is a multiple of p, so med
0 mod p. In the first case med is a multiple of p, so med  0
0  m mod p. In the second case
m mod p. In the second case
where we used Fermat's little theorem to replace mp-1 mod p with 1.
The verification that med  m mod q proceeds in a similar way, treating separately the cases m
m mod q proceeds in a similar way, treating separately the cases m  0 mod q and m
0 mod q and m  0 mod q, using Fermat's little theorem for modulus q in the second case.
0 mod q, using Fermat's little theorem for modulus q in the second case.
This completes the proof that, for any integer m,
Proof using Euler's Theorem
Although the original paper of Rivest, Shamir, and Adleman used Fermat's little theorem to explain why RSA works, it is common to find proofs that rely instead on Euler's theorem.
We want to show med  m mod n, where n = pq is a product of two different prime numbers and e and d are positive integers satisfying ed
m mod n, where n = pq is a product of two different prime numbers and e and d are positive integers satisfying ed  1 mod
1 mod  . Since e and d are positive, we can write
. Since e and d are positive, we can write  for some nonnegative integer h. Assuming that m is relatively prime to n, we have
for some nonnegative integer h. Assuming that m is relatively prime to n, we have
where the last congruence directly follows from Euler's theorem. When 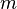 is not relatively prime to
is not relatively prime to  , the argument just given is invalid. However, the desired congruence is still true. Either m
, the argument just given is invalid. However, the desired congruence is still true. Either m  0 mod p or m
0 mod p or m  0 mod q, and these cases can be treated using the previous proof.
0 mod q, and these cases can be treated using the previous proof.
Numerous references which explain RSA using Euler's theorem deal with the case that the message m is not relatively prime to the modulus pq by a misleading probabilistic argument: the proportion of integers mod pq that have a factor in common with the modulus is 1 - (p-1)(q-1)/pq = 1/p + 1/q - 1/pq, which is very small when p and q are large so the chance of the message having a factor in common with the modulus can be considered remote in practice. What is misleading here is that, as the proof with Fermat's little theorem shows, nothing breaks down in the case of messages having a factor in common with the modulus: one has med  m mod n for all m without exceptions. Therefore the correctness of RSA should really be considered an application of Fermat's little theorem rather than Euler's theorem, just as in the original RSA paper.
m mod n for all m without exceptions. Therefore the correctness of RSA should really be considered an application of Fermat's little theorem rather than Euler's theorem, just as in the original RSA paper.
See also
- Public-key cryptography
- Encryption
- Key exchange
- Diffie-Hellman key exchange
- Key management
- Cryptographic key length
- Computational complexity theory
Notes
- ^ a b Rivest, R.; A. Shamir; L. Adleman (1978). "A Method for Obtaining Digital Signatures and Public-Key Cryptosystems". Communications of the ACM 21 (2): 120–126. doi:10.1145/359340.359342. http://theory.lcs.mit.edu/~rivest/rsapaper.pdf.
- ^ a b SIAM News, Volume 36, Number 5, June 2003, "Still Guarding Secrets after Years of Attacks, RSA Earns Accolades for its Founders", by Sara Robinson
- ^ http://www.rsa.com/press_release.aspx?id=261
- ^ Boneh, Dan (1999). "Twenty Years of attacks on the RSA Cryptosystem". Notices of the American Mathematical Society 46 (2): 203–213. http://crypto.stanford.edu/~dabo/abstracts/RSAattack-survey.html.
- ^ Namely, the values of m which are equal to −1, 0, or 1 modulo p while also equal to −1, 0, or 1 modulo q. There will be more values of m having c = m if p − 1 or q − 1 has other divisors in common with e − 1 besides 2 because this gives more values of m such that
 or
or  respectively.
respectively. - ^ Johan Håstad, "On using RSA with Low Exponent in a Public Key Network", Crypto 85
- ^ Don Coppersmith, "Small Solutions to Polynomial Equations, and Low Exponent RSA Vulnerabilities", Journal of Cryptology, v. 10, n. 4, Dec. 1997
- ^ http://www.di-mgt.com.au/rsa_alg.html#pss
- ^ http://www.di-mgt.com.au/rsa_alg.html#weaknesses
- ^ Gary L. Miller, "Riemann's Hypothesis and Tests for Primality"
- ^ 518-bit GNFS with msieve
- ^ RSA-512 certificates abused in-the-wild
- ^ Has the RSA algorithm been compromised as a result of Bernstein's Paper? What key size should I be using?
- ^ Wiener, Michael J. (May 1990). "Cryptanalysis of short RSA secret exponents". Information Theory, IEEE Transactions on 36 (3): 553–558. doi:10.1109/18.54902.
- ^ "Flaw Found in an Online Encryption Method" http://www.nytimes.com/2012/02/15/technology/researchers-find-flaw-in-an-online-encryption-method.html?_r=3&pagewanted=1&hp
- ^ "Ron was wrong, Whit is right" http://eprint.iacr.org/2012/064.pdf
- ^ https://freedom-to-tinker.com/blog/nadiah/new-research-theres-no-need-panic-over-factorable-keys-just-mind-your-ps-and-qs
- ^ Remote timing attacks are practical. . SSYM'03 Proceedings of the 12th conference on USENIX Security Symposium.
- ^ http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.80.1438&rep=rep1&type=pdf
- ^ FaultBased Attack of RSA Authentication
References
- Menezes, Alfred; Paul C. van Oorschot; Scott A. Vanstone (October 1996). Handbook of Applied Cryptography. CRC Press. ISBN 0-8493-8523-7.
- Cormen, Thomas H.; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein (2001). Introduction to Algorithms (2e ed.). MIT Press and McGraw-Hill. pp. 881–887. ISBN 0-262-03293-7.
External links
- The Original RSA Patent as filed with the U.S. Patent Office by Rivest; Ronald L. (Belmont, MA), Shamir; Adi (Cambridge, MA), Adleman; Leonard M. (Arlington, MA), December 14, 1977, U.S. Patent 4,405,829.
- PKCS #1: RSA Cryptography Standard (RSA Laboratories website)
- The PKCS #1 standard "provides recommendations for the implementation of public-key cryptography based on the RSA algorithm, covering the following aspects: cryptographic primitives; encryption schemes; signature schemes with appendix; ASN.1 syntax for representing keys and for identifying the schemes".
- Thorough walk through of RSA
- Prime Number Hide-And-Seek: How the RSA Cipher Works
- Menezes, Oorschot, Vanstone, Scott: Handbook of Applied Cryptography (free PDF downloads), see Chapter 8
- Onur Aciicmez, Cetin Kaya Koc, Jean-Pierre Seifert: On the Power of Simple Branch Prediction Analysis
- A New Vulnerability In RSA Cryptography, CAcert NEWS Blog
- Example of an RSA implementation with PKCS#1 padding (GPL source code)
- Kocher's article about timing attacks
- Online RSA encryption application (Dutch)
- An animated explanation of RSA with its mathematical background by CrypTool
|
|||||||||||||||||||||||||||||


 .
.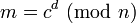 .
. ,
,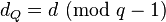 and
and .
.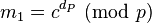
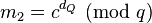
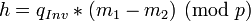 (if
(if 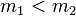 then some libraries compute h as
then some libraries compute h as 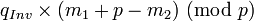 )
)
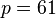 and
and  .
.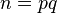 giving
giving
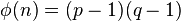 giving
giving
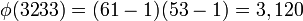 .
. that is
that is 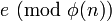 yielding
yielding
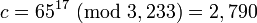 .
.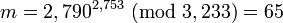 .
.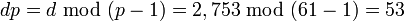
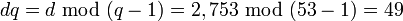
 (Hence:
(Hence:  )
)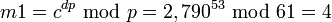

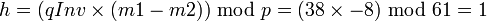
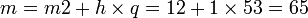 (same as above but computed more efficiently)
(same as above but computed more efficiently) ) and small values of the
) and small values of the 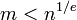 ) the result of
) the result of  is strictly less than the modulus
is strictly less than the modulus 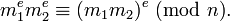 Because of this multiplicative property a
Because of this multiplicative property a  for some value
for some value 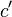 is the encryption of
is the encryption of  . Hence, if the attacker is successful with the attack, he will learn
. Hence, if the attacker is successful with the attack, he will learn  with the modular inverse of
with the modular inverse of 





 or
or  respectively.
respectively.