Problem Set 2, Due Tues. Feb. 5 in Class
(late papers OK until 1:00 Wednesday)
Please put your papers in the mailbox (DRL 4W3) of our TA
Yansong Gao
- The next three players in a game win 30%, 20% and 25% of the
time, respectively. What is the likelihood that none of them
will win this time?
[Equivalent wording: It is the fifth inning of a baseball game. The
batting averages of the next three batters are .300,
.200, and .250. Say they face an average pitcher. What
is the likelihood that none of them will get a hit this
inning?]
-
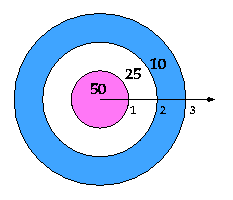 A big dart board consists of three concentric disks of radius 1, 2,
and 3 feet. If a dart lands in the center disk you get 50 points. If
it lands in the middle ring you get 25 points, while if it lands in
the outer ring you get 10 points.
A big dart board consists of three concentric disks of radius 1, 2,
and 3 feet. If a dart lands in the center disk you get 50 points. If
it lands in the middle ring you get 25 points, while if it lands in
the outer ring you get 10 points.
Compute both the expected value and standard deviation of the
number of points you'll get by throwing darts at random at this board.
- a) In a certain town there are 2 bus companies whose buses stop at
the Main Street station. One company's busses run every 8 minutes,
the other runs every 10 minutes -- but the times of arrival of the
previous busses are unknown. The question is, what is the average
length of time that you will wait for a bus after arriving at the
station?
b). Same as the above, but 3 bus companies -- whose busses each stop
every 10 minutes.
- You are interviewing 6 candidates for a job. As you proceed, you
determine the relative ranks of the candidates (you won't know the
"true rank" until you have interviewed all of them). Thus, if there are
6 candidates with true rank 6, 1, 4, 2, 3, 5, then after interviewing
the first three candidates you would rank them 3, 1, 2. Alas, after you
interview a candidate, you either hire that person or the candidate
leaves and can no longer be considered.
You want a strategy when to stop and accept a candidate,
maximizing the likelihood of getting the best candidate. Assume there
are 6 candidates, and they arrive in a random order.
a) What is the probability that you get the best candidate if you
interview all of the candidates? What if you immediately choose the
first candidate?
b) Say you adopt the strategy of interviewing the first half of
the candidates and then accept the first of the following candidates
who is better than any seen so far (if you have seen all the
candidates so are at the last candidate then by these rules you must
accept that person). Show (by a crude estimate) that you have
a chance of less than 50% of getting the the best candidate -- but
better than a 25% chance of getting the the best candidate.
SOLUTION:
Using this strategy you win if the second best candidate is in
the first group of 5 and the best candidate is in the last group of 5,
so 25% of the time.
- In the
Cancer Test Case, we used that everyone who has the cancer tests
positive. Instead, say 5% of those who have the cancer test negative (false
negative). Of those who test negative, what is the likelihood that
they have this cancer?
- [Monty Hall Problem] Suppose you're on a
game show, and you're given the choice of three doors: Behind one door
is a car; behind the others, goats. You pick a door, say No. 1, and
the host, who knows what's behind the other doors, opens another door,
say No. 3, which has a goat. He then says to you, 'Do you want to pick
door No. 2?' Is it to your advantage to switch?
What should you do -- and why? A "tree diagram" may be useful.
Discussion
- In an oft-cited experiment the psychologists Kahneman and
Tversky asked a group of subjects to imagine the outbreak of an
unusual disease, expected to kill 600 people, and to choose between
two public health programs to combat it.
Program A, the subjects were told, had 400 people would die.
Program B had a one-third probability that no one would die and a
two-thirds probability that 600 people would die
Which would you choose? Explain your decision.
- a). Would you accept a gamble that offers a 10-percent chance to
win $95 and a 90-percent chance to lose $5?
b). Would you pay $5 to participate in a lottery that offers a
10-percent chance to win $100 and a 90-percent chance to win nothing?
c). Do the options in a)-b) offer identical outcomes?
Remarks:
a). The great majority of people in the study rejected this
proposition as a loser.
b)-c). A large proportion of those who refused the first option
accepted the second. But the options offer identical outcomes. As
Kahneman and Tversky see it: "Thinking of the $5 as a payment makes
the venture more acceptable than thinking of the same amount as a
loss." It's all a matter of how the situation is framed in this case,
the extent to which people are "risk averse."
Bonus Problem Please give your solutions directly to Dr. Kazdan
B-1. [Blood Test] A number, k, of people are subjected to a
blood test, the result of which is either "positive" or "negative".
It can be processed in two ways:
i). Each person can be tested separately, so k tests are required.
ii). The blood samples of all k people can be pooled and
analyzed together. If this test is negative, then one test suffices
for the k people, while if the test is positive, each of the
k people must be tested separately so k+1 tests are
then required.
Assume that the probability, p, that a test is positive is
the same for all people and that these events are all independent.
a). Find the probability that the test for a pooled sample of k
people will be positive.
b). What is the expected value of the number of tests necessary
under plan ii).?
SOLUTION:
ExpectedVal =1(1-p)k + (k+1)[1-(1-p)k]
c). A large number, N, of people are subjected to a
blood test, the result of which is either "positive" or "negative",
just as above. The plan is to run the blood tests in batches
of k people [assume that N is divisible by k].
Compute the expected value of the number of blood tests needed.
SOLUTION:
ExpectedVal = (N/k){1(1-p)k + (k+1)[1-(1-p)k]}
= N[1 - (1-p)k + (1/k)]
d). For small p, show that the value of k that will
minimize the expected number of tests made under plan ii). is
approximately 1/√p.
SOLUTION
Take the derivatve with respect to k.
Reference:
Pooled Tests
 A big dart board consists of three concentric disks of radius 1, 2,
and 3 feet. If a dart lands in the center disk you get 50 points. If
it lands in the middle ring you get 25 points, while if it lands in
the outer ring you get 10 points.
A big dart board consists of three concentric disks of radius 1, 2,
and 3 feet. If a dart lands in the center disk you get 50 points. If
it lands in the middle ring you get 25 points, while if it lands in
the outer ring you get 10 points.