Possible Topics
- Understand the meaning of "average" of a data sample. In what sense is
the usual "mean" a good measurement of the "average"? See
Sex Bias in Grad Admissions?
How can one treat data when some of it is less trustworthy? Generalize these ideas to least squares regression, both for straight lines and other curves. - Understand the "expected value" of an action. For instance, in a
football game, when is it appropriate to try for a two-point conversion?
See
NYT 1/16/00 article.
- Understand the "law of large numbers". How large should a statistical
sample be? Especially in an election year, it is easy to find examples and
applications in the news all the time.
One says that two people are more closely related if they have more genes in common. Is a woman more closely related to her uncle or her grandmother? Why? - Assume the earth is a sphere and you know the longitute and
latitude of two cities, both at sea level. Find a formula for the
(flying) distance between them. [Since the radius of the eartn is
about 4000 miles and the height of Mt. Everest is roughly 5.5 miles,
there is essentially no error if you assume all cities are at sea
level.]
- Assume the orbit of the earth is a circle around the sun. Find a
formula for the number of hours of daylight at a certain location on
earth. It should involve the latitude and day of the year. [To a good
approximation, on any given day, points at the same latitude will have
the same number of hours of daylight on a given day.]
- Would it pay to tow an iceberg from Greenland to sell ice in Florida?
Here, one must make a mathematical model and use it for computations. What
are the significant assumptions? What has been ignored? Does the model
result in a mathematics problem that is amenable to hand or machine
computation?
- When is it appropriate to divide data points into groups and then fit
them with splines, rather than attempt a regression or a fit of the entire
data set? How is this done?
- Understand a predator-prey model. This usually involves setting up
and solving a system of ordinary differential equations. These are
especially amenable to computer experiments and the results can be
presented for non-experts on the Web. This is related to biological
synchronization below.
- To understand some programming issues, especially on the Web, students
could attempt to write a program that accepts students' grades on an exam,
and displays a histogram of the results. After allowing the instructor to
input cutoffs for A, B, C, etc, the program could calculate the grade
point average of the class. Then a second program would let students
access their own exam grades as well as the summary data for the entire
class. How can this be done to insure privacy?
- This could be the jumping-off point for a mathematical discussion of
how such a scheme might be used to devise an on-line voting system.
Here is a simple version: Vote Here
A more complicated such project would be to write a program that allows someone to take a multiple-choice exam on-line and have the score returned immediately. An example is a Diagnostic Exam for this very course.
- The theory of elections presents another fascinating mathematical problem.
Despite one's intuitive suspicions, it is not known how to devise a fair
election. Arrow's Theorem states that the only procedure satisfying a
short list of seemingly innocent conditions is a dictatorship!
Arrow subsequently won the 1972 Nobel Prize in Economics, in part for
this theorem.
Some of the difficulties are illustrated by a simple example. Say there are three candidates: Susan, Tom, and Alice. There was to be a primary election between two of the candidates and then have another election between the winner and the third candidate. Say one knows the following vote preferences:
between Susan and Tom: Susan 150 votes, Tom 130 votes between Susan and Alice: Susan 135 votes, Alice 145 votes between Tom and Alice: Tom 143 votes, Alice 137 votes
If the primary election is between Susan and Tom, then Susan wins but then Alice wins the runoff. However if the primary election is between Susan and Alice, then Alice wins but looses to runoff to Tom. Similarly, if the primary is between Tom and Alice, then Susan eventually wins. Thus, the winner if the election depends on how it is administered. Not so fair. How should one run a fair election?Examples of Voting Procedures
Some articles discussing voting. - Markov chains. Here are two typical homework problems:
- There are two local branches of the Limousine Rental Company,
one at the Airport and one in the City, as well as branches Elsewhere.
Say every week of the limousines rented from the Airport 25% are returned to the City and 2% to branches located Elsewhere. Similarly of the limousines rented from the City 25% are returned to Airport and 2% to Elsewhere. Finally, say 10% of the limousines rented from Elsewhere are returned to the Airport and 10% to the City.
If initially there are 35 limousines at the Airport, 35 in the City, and 150 Elsewhere, what is the long-term distribution of the limousines? -
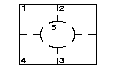 One model for a rat in a maze states that at the end of
every hour the rat leaves its current ``room'' through any doorway and is
equally likely to go to any of the adjacent rooms. (We assume it never
stays where it is).
One model for a rat in a maze states that at the end of
every hour the rat leaves its current ``room'' through any doorway and is
equally likely to go to any of the adjacent rooms. (We assume it never
stays where it is).
In the long-term, what percentage of the time is it in each room?
- There are two local branches of the Limousine Rental Company,
one at the Airport and one in the City, as well as branches Elsewhere.
- Study synchronization in nature:
In southeast Asia, male fireflies flash in unison, creating a beacon that can be seen miles away. Pendulum clocks hanging on the same wall will tend to swing together. Ten thousand cells in your heart discharge electrical signals simultaneously to tell your heart when to beat.
In concert halls of Eastern Europe. after a performance, applause starts as tumultuous cacophony, then suddenly transforms into synchronized clapping (WAV recording [0.8Mb]).
For an introduction, see Scientific American, Dec. 1993, pp. 102-109.- You are interviewing 100 applicants for a job. At the conclusion of each interview, you can either hire that applicant or not. If you do not, that applicant leaves and you have no future opportunity to hire that person.
Is there a clever strategy to use? This sounds vague, but something smart can really be said.- The Monty Hall problem. Do some computer simulations to understand the issues. Then attack the theory.
- Suppose that you undergo a medical test for a relatively rare cancer. Medical statistics show that the cancer has an incidence of 1% among the general population. Thus, before you take the test, and in the absence of any other evidence, your best estimate of your likelihood of having the cancer is 1 in 100.
Then you take the test. Extensive trials have shown that the reliability of the test is 79%. More precisely, although the test does not fail to detect the cancer when it is present, it gives a positive result in 21% of the cases where no cancer is present -- this is known as a false positive. When you are tested, the test produces a positive diagnosis.
The question is: Given the result of the test, what is the probability that you have the cancer?Most people assume that if the test has a reliability rate of nearly 80%, and they test positive, then the likelihood that they have the cancer is about 80%. But they are way off. Given the scenario just described, the likelihood that they have the cancer is a mere 4.6%). Still a worrying possibility, but hardly that scary 80%. We'll learn when and how to do these computations. [The source of this paragraph is The Legacy of the Reverend Bayes by Keith Devlin. A bit more information is there.]
- The spruce budworm attacks the leaves of the balsam fir tree in eastern Canada. These insects can defoliate a forest in four years. We make a mathematical model to help understand this. This understanding may guide us to control future outbreaks.
- In many countries, including the U.S.A., it is traditional to give children the family name of their father. Thus, if there are insufficient male children, the family name will die out. How likely is this to happen? To take a specific example, say at each generation there is a 50% chance of no male offsprings, 25% chance of one male and 25% chance of two makes.
- Making decisions. In real life, one frequently must make a choice between various alternatives: "Which house should I buy? "What college should I attend?" "Which job should I take?" "In what direction should my company expand?" We will discuss some quantitative approaches to this, including deciding if a quantitative approach is absurd.
Web search engines, such as Google, also make similar decisions in attempting to present you with an ordered list of the most appropriate web pages matching your search request. The mathematics is remarkably similar.- Linear Optimization. Here is an example. You are a traveling snake-oil salesman, selling brand A at $5 dollars per gallon and brand B at $3 dollars per gallon. You ply your trade in a territory that craves snake oil, so you can be sure of selling all you carry at the prices mentioned. Things are not quite so simple, however. Snake oil requires the magical ingredient M. More precisely, brand A requires 4 ounces of ingredient M per 100 gallons of oil, and brand B requires 3 ounces per 100 gallons. And you have only 12 ounces of ingredient M.
If the scarcity of ingredient M were the only constraint, it would be easy to see that you would maximize gross income by producing and selling only brand A. There is, however, one more fly in the ointment. Brand A weighs 15 pounds per gallon and brand B weighs one-third this much. You are capable of transporting only 3,000 pounds of snake oil. How much should be brand A and how much brand B?- An introduction to the Theory of Games.
- Encrypting files and email on the Internet, an introduction to the RSA algorithm.
- How does the search engine Google process your Internet search requests?
- A recent investigation concerning breast cancer. For background one can first read the following New York Times article. This refers to an AMA Article
This list of topics is obviously tentative and more topics present themselves all the time. It is easy to imagine segments of the course that will change from semester to semester in response to such stimuli. - You are interviewing 100 applicants for a job. At the conclusion of each interview, you can either hire that applicant or not. If you do not, that applicant leaves and you have no future opportunity to hire that person.