Selected Answers to Problem Set 9

---

4. To solve this, put the information into a matrix such that, and let v = [0 0 1] be our original vector. Then for any hour n, the probability that the rat will be in each room is defined as (A^n)v. Take the sum of n*(A^n)v, as n goes from 1 to infinity (on Maple, going up to about 50 should suffice). The first coordinate of the vector increases to infinity (as we should believe to be so, since the odds of the rat being in room 1 after a hundred hours is near 100%), but odds that the rat isn't in room one approaches eleven hours (add an extra hour for the first one, which isn't accounted for in the equation), which is our answer.

Here's a script demonstrating a simulation of the rat maze problem.

evalf(evalm(sum('evalm(A^n&*v)',n=1..20)));
            [11.15804200, 2.644481648, 6.197476351]

evalf(evalm(sum('evalm(A^n&*v)',n=1..50)));
           [40.04541293, 2.986058251, 6.968528817]

evalf(evalm(sum('evalm(A^n&*v)',n=1..100)));
           [90.00020556, 2.999936893, 6.999857547]

---

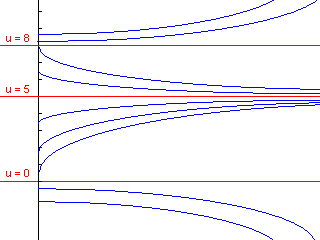
6.  First realize that u' has roots at u={0,5,8}, so if u equals any of these, then u' is zero
      and it remains constant at that value.  This means that the graph of u' cannot cross these
      values, but rather approaches these lines.
    If 0 < u(0) < 5, then u' is a product of three positive values, so u' is positive.
      As t approaches infinity, lim u(t) = 5-.
    If 5 < u(0) < 8, then u' is a product of two positive and one negative values, so u' is negative.
      As t approaches infinity, lim u(t) = 5+.
    If u(0) > 8, then u' is a product of two negative and one positive values, so u' is positive.
      As t approaches infinity, lim u(t) = +infinity.
    If u(0) < 0, then u' is a product of three negative values, so u' is negative.
      As t approaches infinity, lim u(t) = -infinity.
    u(t) has stable points at u = 5, and unstable points at u = {0,8}.

---