Selected Answers to Problem Set 7

1. Algebraically, we know that the number of yes's equal 80% of the yes's plus 40% of the no's. Likewise, we know that the number of no's equal 20% of the yes's plus 60% of the no's. 
y = 0.8y + 0.4n
n = 0.2y + 0.6n

y - y = 0.8y - y + 0.4n
n - n = 0.2y + 0.4n - n

0.2y = 0.4n
0.2y = 0.4n  (also knowing that y + n = 1)

-> y = 2/3, n = 1/3
2. Algebraically, this problem is set up similar to the previous problem: 
a = 0.73a + 0.25c + 0.10e
c = 0.25a + 0.73c + 0.10e
e = 0.02a + 0.02c + 0.80e
a = 100, c = 100, e = 20 (knowing that a + c + e = 220).
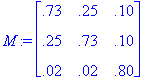
Taking M^20, we get a similar result:
3. The matrix would take this form, coming from the algebraic equations: 
a = (7/12)a + (1/6)b
b =  (1/6)a + (1/2)b
c =  (1/4)a + (1/3)b + c
Taking A100 we can understand the state of equilibrium:
which basically is the matrix with ones on the bottom row and zeroes everywhere else. This implies that the equilibrium state has everyone dropping out of chemistry. All the vectors P that satisify AP = P are of the form R * [0 0 1], or all the vectors along the x3axis (or the z-axis, if you prefer).
4. Click here for a pdf file explaining how the product of any two markov matrices is a markov matrix. This file was produced using LaTeX, a markup language (not too dissimilar to HTML) used primarily for formatting scientific (and non-scientific) publications. The source can be found here as well for your viewing pleasure.

Counterexample:

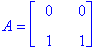
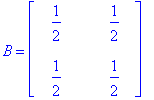
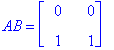
Clearly, B has all positive elements, both A and B are markov matrices, but AB does not have all positive elements. It is however, as we have seen in the previous part, a markov matrix. If all the elements in A are positive (holding still that A and B are markov matrices), then AB will always have all positive elements (no zeroes).

5. Basically, with the matrix from before, alter it so that room one absorbs the other rooms, meaning that no rooms should get any input from room one, and room one's output is solely to room one.
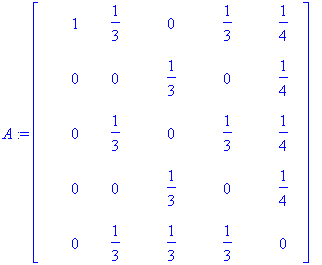
This matrix implies that the rat will eventually end up in room one, which should be no surprise, since it can enter from any given starting location, and it doesn't leave once it enters there. So eventually the rat will enter room one and never leave.
6. With two rooms, the rat has a 30% chance of moving out. Therefore, we want to find the expected time the rat will be in room 2. 
Staying	for	Chance of Staying
1 hour		30%
2 hours		70% * 30%
3 hours		70% * 70% * 30%
n hours		(70%)n*30%
We take this summation as n goes from 1 to infinity:
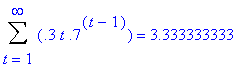
For three rooms, we can take both room separately. For rooms two and three, 
Room 2		Chance of Staying x hours
1 hour		50%
2 hours		50% * 50%
3 hours		50% * 50% * 50%		Expected waiting time: Two hours
n hours		(50%)n

Room 3		Chance of Staying x hours
1 hour		50% * 50%
2 hours		50% * 50% * 50%
3 hours		50% * 50% * 50% * 50%	Expected waiting time: One hour
n hours		(50%)n+1
Basically, in order for the rat to stay in room 2 for one hour, the rat has to move into room one at the first door opening (50%). To stay for two hours in room two, it has to move into room three (50%), then move into room one when it moves back (50% * 50%, 25%). For the rat to stay in room three for one hour, the rat has to move into room three (50%), then move into room one after moving back into room two (50% * 50%, 25%). And so on...
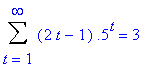
7. As k tends to infinity, yk+1 = yk and zk+1 = zk. 
y = 0.8y + 0.3z
z = 0.2y + 0.7z

0 = -0.2y + 0.3z
0 =  0.2y - 0.3z

2y = 3z
y + z = 5     =>     y = 3, z = 2.
b) We can show this by induction. At k = 1, B = SDS-1. Then, assuming that Bk = SDkS-1, we wish to show that Bk+1 = SDk+1S-1: 
BkB = SDkS-1SDS-1
    = SDkDS-1
    = SDk+1S-1
Were these answers helpful?
Yes
No
 Name (optional):