Selected Answers to Problem Set 4
1. The expected value is the sum of each possible value multiplied by the probability that the value will occur. Each value has a 1/6 chance of occuring. To be correct, the equation below should have 1(1/6) + ... + 6(1/6), but I pulled the 1/6 out.
var = ((1 - 3.5)2(1/6) + (2 - 3.5)2(1/6) + ... + (6 - 3.5)2(1/6))
= 6.25(1/6) + 2.25(1/6) + 0.25(1/6) + 0.25(1/6) + 2.25(1/6) + 6.25(1/6)
= (6.25 + 2.25 + 0.25 + 0.25 + 2.25 + 6.25) / 6
= 17.5 / 6 = 35 / 12
sd = sqrt(var)
= sqrt(35 / 12)
= 1.7078
Rolling 100 dice follows the same pattern. But because these are
independent trials the variance will be multiplied by 100. The standard
deviation, the square root of the variance, will be multiplied by the
square root of the 100.
var = (35 / 12) * 100
sd = sqrt(35 / 12) * sqrt(10)
= 1.7078 * 10 = 17.078
When we take the average, however, we will divide by 100 (for the average
of 100 trials). Conceptually this should make sense: the average of a lot
of dice rolls should be rather tight and shouldn't stray from the expected
value too much.
var = (35 / 12) / 100
sd = sqrt(35 / 12) / sqrt(100)
= 1.7078 / 10 = 0.17078
2. The probability of interviewing all the candidates and taking the best one is, of course, 1. The probability of simply taking the first candidate, if there are six, is 1/6. Of course, if we interview all the candidates and take the last one (the question could be intrepreted this way, I suppose) then the odds are again 1/6.
If we interview the first half of the candidates and then take the next best from the second half, then two things must be true. First, the best candidate must be in the second half. Second, the best candidate must come before any other candidates that are better than the best of the first half. That is, if the order were (1 4 2 5 6 3) then candidate #5 would be chosen because it is the first candidate better than the best of the first half, #4. Taking these two clauses into consideration, if candidate #5 is in the first half and #6 is in the second half we are guaranteed to get #6, for no other candidate is better than #5 except for #6. The odds of #5 being in the first half is 50% (3/6), and if this is true then the odds of #6 being in the second half is 60% (3/5), since #6 can be in three of five possible positions. Taking the product of these two yield a 30% chance, which is greater than 25%. This same process can be repeated to see the odds of #4 being the best candidate of the first half and #6 occuring before #5 in the second half, and likewise to see the odds of #3 being the best candidate of the first half and #6 occuring before both #4 and #5.
Link to Secretary Problem Perl script. This script allows the user to enter the total number of secretaries and the number of secretaries interviewed before taken the next best one.
6.
GC - Guilty of Crime
IC - Innocent of Crime
GT - Guilty on Test
IT - Innocent on Test
P(GT|IC)P(IC)
P(IC|GT) = ---------------
P(GT)
P(GT|IC)P(IC)
= -------------------------------
P(GT|IC)G(IC) + P(GT|GC)P(GC)
(0.02)(88)
= -------------------------
(0.02)(88) + (0.90)(12)
= 1.76 / (1.76 + 10.80)
= 0.14 = 14%
4. The probability that a test for k people will be negative will be (1-p)^k, where 1-p is the probability that one person is negative, multiplied k times. The probability that a test for k people will be positive is the compliment, or 1 - (1-p)^k.
The probability that the test for a pooled sample of k people will be positive is the number of tests done for a negative sample times the probability of a negative sample, plus the number of tests done for a positive sample times the probability of a postive sample.
Tests in negative sample: 1 Prob. of negative sample: (1-p)^k Tests in positive sample: k+1 Prob. of positive sample: 1-(1-p)^k Total probability (and simplified):Here's a Maple worksheet (pdf file) demonstrating the answer to part three of the homework.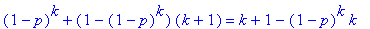
5. First we find the derivative of E(P) and set it equal to zero.
2(p1-P) + ... + 2(p48-P) = 0
(p1-p) + ... + (p48-P) = 0
(p1 + ... + p48) - 48P = 0
P = (p1 + ... + p48) / 48
If we replace p2 by p2+c, we simply alter our equation from above.
2(p2-P) + 2(p2+c-P) + ... + 2(p48-P) = 0
(p1-p) + (p2+c-P) + ... + (p48-P) = 0
(p1 + ... + p48 + c) - 48P = 0
P = (p1 + ... + p48 + c) / 48
This simply equals the previous value we found for P, the average, except
we are adding c/48 into the equation.
3. Same as above--find the derivative and set it equal to zero
2a(p1-P) + ... + 2a(p47-P) + 2b(p48-P) = 0
a(p1-P) + ... + a(p48-P) + b(p48-P) = 0
a(p1+...+p47) + b(p48) - P(47a+b) = 0
a(p1+...+p47) + b(p48) = P(47a+b)
P = [a(p1+...+p47)+b(p48)]/[47a+b]
If we change a trusted value, p2, by p2+c, then we have a similar result
as in problem two. We will get:
P=[a(p1+...+p47+c)+b(p48)]/[47a+b].
If we change a less trusted value, p48, by p48+c, then we again have the
same result:
P=[a(p1+...+p47)+b(p48+c)]/[47a+b].
If we want the data given with the constant a to be twice as reliable as those given with the constant b, then we need to weight the constant a twice as much as constant b (that is, a = 2b). This way, any error given by the less-reliable reporter, p48, will not vary as much as with the other people.
7. A better way would use a formulation similar to weighted averages. Using the standard deviation, we can see how far the student's test scores were from the mean, divide by the standard deivation, and take the average of the three scores. By using the standard deviation we take in to account the relative difficulty of the test (as reported by the other test scores in the class).
To find the lowest grade we simply drop the lowest corrected score. In this case, the third test was the lowest corrected score. Make a quick check to see that this is correct. The new score, after removing the lowest corrected score, should be higher than the previous score.