Selected Answers to Problem Set 10
1. The equation d/dt p(t) should read as 4p - p = 3p. It has an equilibrium point at p = 0. When p > 0, dp/dt is positive, so the population will increase without bound (this is according to this equation; other factors will no doubt stop the unbounded growth).
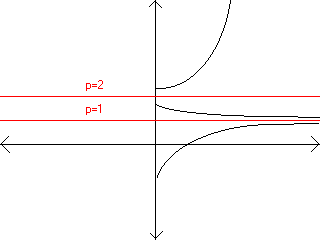
2. The function doesn't grow (dp/dt = 0) when p=1 or p=2. So we have two equilibrium
points at p=1 and p=2. Looking at the plot of dp/dt = (p-1)(p-2) we can see that dp/dt
is positive when p < 1, dp/dt is negative when p > 1 and p < 2, and dp/dt is positive
when p > 2. This means that p=1 is a stable equlibrium point and p=2 is an unstable
equlibrium point (Excuse the crudeness of the drawing).
3 & 4. Graph i) has zeros at {-3, 2}. At values less than -3, the derivative is negative and values between -3 and 2 the derivative is positive. Therefore we know that -3 is an unstable equilibrium point. At values greater than 2 the derivative is negative. Therefore we know that 2 is a stable equilibrium point. If x(0) = 1, then x(t) approaches 2 as t gets very large. If x(0) = -4 then x(t) approach -infinity. If x(0) = -1 then x(t) approaches -infinity.
Graph ii) has zeros at {-2, 0} and the same method applies. And from here, a general rule of thumb can be applied. If, through a zero, the graph of the derivative goes from negative to positive, that zero is an unstable equilibrium point. If the graph goes fron positive to negative, that zero is a stable equilibrium point. Therefore, at -2 it goes from positive to negative and -2 is a stable equilibrium point. At 0 it goes from negative to positive so 0 is an unstable equilibrium point. If x(0) = 1 then x(t) approaches infinity. If x(0) = -4 then x(t) approaches -2. If x(0) = -1 then x(t) approaches -2.
Graph iii) has zeros at {-2, 2, 4}. At -2 it goes from positive to negative so it's a stable equilibrium point. At 2 it's an unstable equilibrium point at and 4 it's stable. If x(0) = 1 then x(t) approaches -2. if x(0) = -4 then x(t) approaches -2. if x(0) = -1 then x(t) approaches -2. In fact, any values less than 2 will approach -2 and values greater than 2 will approach 4. Question--what happens if x(0) = 2?
Graph iv) has zeros at {-3, -2, 0, 3}. At -3 it goes from negative to positive so it's an unstable equilibrium point. At -2 it's stable, at 0 it's unstable and at 3 it's stable. If x(0) = 1 then x(t) approaches 3. If x(0) = -4 then x(t) approaches -infinity. If x(t) = -1 then x(t) approaches -2. The pattern of stable/unstable equilibrium points works for graphs without double roots. What happens with double roots?