Selected Answers to Problem Set 9
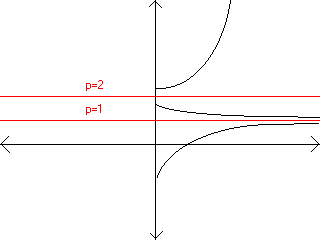
2. The function doesn't grow (dp/dt = 0) when p=1 or p=2. So we have two equilibrium
points at p=1 and p=2. Looking at the plot of dp/dt = (p-1)(p-2) we can see that dp/dt
is positive when p < 1, dp/dt is negative when p > 1 and p < 2, and dp/dt is positive
when p > 2. This means that p=1 is a stable equlibrium point and p=2 is an unstable
equlibrium point (Excuse the crudeness of the drawing).
4 & 5. Graph i) has zeros at {-3, 2}. At values less than -3, the derivative is negative and values between -3 and 2 the derivative is positive. Therefore we know that -3 is an unstable equilibrium point. At values greater than 2 the derivative is negative. Therefore we know that 2 is a stable equilibrium point. If x(0) = 1, then x(t) approaches 2 as t gets very large. If x(0) = -4 then x(t) approach -infinity. If x(0) = -1 then x(t) approaches -infinity.
Graph ii) has zeros at {-2, 0} and the same method applies. And from here, a general rule of thumb can be applied. If, through a zero, the graph of the derivative goes from negative to positive, that zero is an unstable equilibrium point. If the graph goes fron positive to negative, that zero is a stable equilibrium point. Therefore, at -2 it goes from positive to negative and -2 is a stable equilibrium point. At 0 it goes from negative to positive so 0 is an unstable equilibrium point. If x(0) = 1 then x(t) approaches infinity. If x(0) = -4 then x(t) approaches -2. If x(0) = -1 then x(t) approaches -2.
Graph iii) has zeros at {-2, 2, 4}. At -2 it goes from positive to negative so it's a stable equilibrium point. At 2 it's an unstable equilibrium point at and 4 it's stable. If x(0) = 1 then x(t) approaches -2. if x(0) = -4 then x(t) approaches -2. if x(0) = -1 then x(t) approaches -2. In fact, any values less than 2 will approach -2 and values greater than 2 will approach 4. Question--what happens if x(0) = 2?
Graph iv) has zeros at {-3, -2, 0, 3}. At -3 it goes from negative to positive so it's an unstable equilibrium point. At -2 it's stable, at 0 it's unstable and at 3 it's stable. If x(0) = 1 then x(t) approaches 3. If x(0) = -4 then x(t) approaches -infinity. If x(t) = -1 then x(t) approaches -2. The pattern of stable/unstable equilibrium points works for graphs without double roots. What happens with double roots?
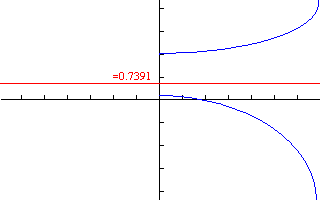
8. if dx/dt = x - cos x, then the equilibrium points are when dx/dt = 0, or when x = cos x. This happens when x
= 0.7391. Whether this is stable or unstable depends on whether x - cos x is less than or greater than zero for values
x < 0.7391 and x > 0.7391. If x < 0.7391, then x - cos x is negative, and if x > 0.7391, then x - cos x is positive.
Therefore, at 0.7391, it changes from negative to positive and that means 0.7391 is an unstable equilibrium point. If
x(0) = 2, then x(t) approaches infinity for large t, and if x(0) = 0.1, then x(t) approaches -infinity for large t.