Selected Answers to Problem Set 5

1. First we find the long-term distribution of the matrix, then we can plug in the initial values. Basically we have a vector P(n) at some time n. After one period, the vector will be P(n+1), which is AP(n). For the long-term distribution, P(n+1) = P(n), or P=AP.

a = 0.73a + 0.25c + 0.10e
c = 0.25a + 0.73c + 0.10e
e = 0.02a + 0.02c + 0.80e

The coefficients can be put into this matrix A, and P = . If P=AP, then AP-P = 0, or P(A-I) = 0. Good old eigenvalues will come to play. If you have Maple, you can plug this matrix into a variable and take it to a very high power to get that = <5/11 5/11 1/11>, or 100 cars at both the airport and the city, and 20 cars everywhere else. If you don't have maple, you can solve this using Gauss-Elimination: subtract a,c,e from both sides of the three equations so that each equals zero.

| -0.27  0.25  0.10 | 0 |
|  0.25 -0.27  0.10 | 0 |
|  0.02  0.02 -0.20 | 0 |

---

2. For a sample 3x3 matrix:

If we add up the columns (to check if it's a Markov matrix) we can factor the sums:

Since we know that the columns in A and B add up to 1, we know that the product of the sums in AB is also 1. Hence, AB, or the product of a 3x3 matrix, is also a Markov matrix.

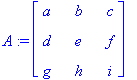
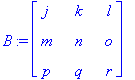
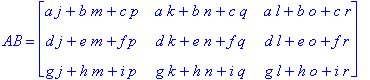
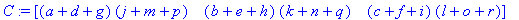
Now we must show this for an n x n matrix:

| a11 ... a1n | | b11 ... b1n |
| ... ... ... | | ... ... ... |
| an1 ... ann | | bn1 ... bnn |

| a11b11 + ... + a1nbn1 ... a11b1n + ... + a1nbnn |
| ..................... ... ..................... |
| an1b11 + ... + annbn1 ... an1b1n + ... + annbnn |

The sum of column one (and the same for subsequent columns) is:

a11b11 + ... + a1nbn1 + an1b11 + ... + annbn1
a11b11 + an1b11 + ... + a1nbn1 + annbn1
b11(a11 + ... + an1) + ... + bn1(a1n + ... + ann)
b11 + ... + bn1
1

---

6. F(X) is a function on a vector X. We must show that it comes in the form of a matrix.

F(X)	= F(xi + yj)
	= F(xi) + F(yj)
	= xF(i) + yF(j)
	= x(ai + bj) + y(ci + dj)
	= (ax + cy)i + (bx + dy)j
	= | ax bx | | i |
	| cy dy | | j |