Selected Answers to Problem Set 3
1. Link to Day of the Week Webpage. The webpage is dotw.html and a copy of the Perl script is dotw2.pl. This script accepts absurd dates (like Feb. 30th). Slight modifications can be made to accomodate these entries, but then you would have to return the user to the original page; it's not a difficult process, but it's not necessary for the class at this point.
2. The math approach: if I choose a door at random, it is clear that I have a 33% chance at guessing the right door. Now, if I do not change my guess, then the door I chose still has a 33% chance at being right. If I switch, then that leaves one other door. The door I had guessed at the beginning had a 33% chance of being right and the opened door now has a 0% chance of being right. Therefore, the other unopened door as a 67% chance of being the right door. It is in my best interest to always switch.
Link to Monty Hall Problem Perl Script. The first script simulates no switching, the second emulates switching.
3) One of my favorite problems of the year. The probability of interviewing all the candidates and taking the best one is, of course, 1. The probability of simply taking the first candidate, if there are six, is 1/6. Of course, if we interview all the candidates and take the last one (the question could be intrepreted this way, I suppose) then the odds are again 1/6.
If we interview the first half of the candidates and then take the next best from the second half, then two things must be true. First, the best candidate must be in the second half. Second, the best candidate must come before any other candidates that are better than the best of the first half. That is, if the order were (1 4 2 5 6 3) then candidate #5 would be chosen because it is the first candidate better than the best of the first half, #4. Taking these two clauses into consideration, if candidate #5 is in the first half and #6 is in the second half we are guaranteed to get #6, for no other candidate is better than #5 except for #6. The odds of #5 being in the first half is 50% (3/6), and if this is true then the odds of #6 being in the second half is 60% (3/5), since #6 can be in three of five possible positions. Taking the product of these two yield a 30% chance, which is greater than 25%. This same process can be repeated to see the odds of #4 being the best candidate of the first half and #6 occuring before #5 in the second half, and likewise to see the odds of #3 being the best candidate of the first half and #6 occuring before both #4 and #5.
Link to Secretary Problem Perl script. This script allows the user to enter the total number of secretaries and the number of secretaries interviewed before taken the next best one.
4. Here's a Maple Worksheet with the answer (Adobe PDF File). Although the answer is given as -44/15 and -2/5 don't worry about the negative aspect. It should be evident that the answer would never be negative; it's just the way it came out on Maple.
Link to Bus Problem Perl Script. This script allows the user to enter the number of busses involved and the frequency of each bus. It then computes the average waiting time.
5. The Algebraic Solution: On a stick of length one, the conditions are such:
i) If I assign c to be the longest, then a + b > c ii) if a + b + c = 1, then a + b = 1 - c iii) By substitution, 1 - c > c, or c < 0.5 iv) Therefore, the longest piece must be shorter than 0.5, and all piece therefore must be shorter than 0.5.Knowing these to be true, for any cut x that I make on the stick, it denotes a range of possible cuts that will yield three pieces which will make a triangle (that is, three pieces all of which are less than 1/2).
i) x < 1/2 ii) y - x < 1/2 implies y < x + 1/2 iii) 1 - y < 1/2 implies y > 1/2 iv) Therefore, 1/2 < y < x + 1/2From this, we can see that if we make a cut x then the odds that y will fall in between 1/2 and (x + 1/2) is exactly x. Of course, we cannot make a cut past one, so when x is past 1/2, y will be between (x - 1/2) and 1/2 (visualize flipping the stick around - if our first cut is past the halfway mark, flip the stick and it's now before the halfway mark). We can instead take the integral of all values of x between 0 and 1/2 and multiply by two (in the picture c1 should be x).
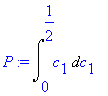
P, then, equals 1/8. Multiplied by two (as stated above) gives us the answer, 1/4, or 25%.
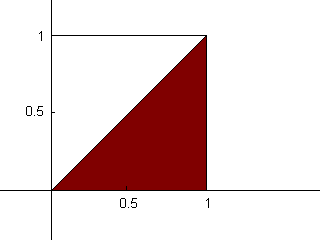
The Graphical Solution: If we make a two-dimensional graph with the
x-coordinate as our first cut and y-coordinate as our second cut, we can
find where on the graph two correct cuts can be made. First, if we assume
that our second cut will be larger than our first cut, we divide our
triangle in half. The red part of the graph is where x, our first cut, is
larger than y, our second cut.
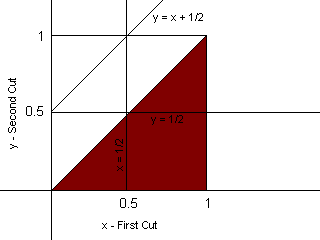
Now, from this we'll make three lines, one for x = 1/2, one for y = 1/2, and one for y = x + 1/2. Basically we're going to find the areas where x < 1/2, y < 1/2, and y - x < 1/2.
With these lines, we shade appropriately to find these three inequalities.
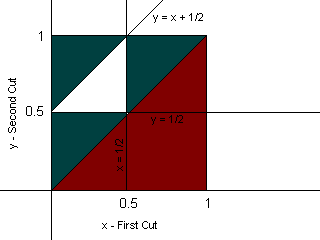
From this, we can see that the white space in the middle has an area of 1/8, and this is out of a possible 1/2 (remember we're not looking at the red part of the graph, as this is when the first cut is larger than the second cut). 1/8 / 1/2 = 1/4 or 25%.
Link to Stick Problem Perl Script. This script doesn't all the user any input, but simply calculates simultaneously the three methods described above the probablility of creating a triangle.
Extra Credit
Part b: Cutting from the rest of the stick: as above, if we make a cut at
x, then the probability of cutting a second good cut is x / 1 (one being
the length of the stick. In this new case, the length of the stick is 1 -
x, so we have to take the integral from 0 to 1/2 (because if we cut after
1/2 we definitely can't make a stick) of x / (1 - x). This comes out to
be about 19%.
Part c: Cutting from the larger half of the stick. Same as part b, except
we're taking the integral from 0 to 1 (because now, if we cut past 1/2,
then we simply flip the stick around and cut from the larger side). We
take the integral from 0 to 1 of x / (1 - x) which yields about
38%.
6. First, the answer:
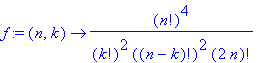
How did I ever get this!? you may ask. We'll take it step by step. Let's say that we have five red marbles and five white marbles, ten in all. Let's try to choose three red marbles. At first our odds are 5/10 to choose a red marble. After that, it's 4/9, then finally it's 3/8. Now, to pick two white marbles, the odds are 5/7, then 4/6. Multiplying these all together we get:
(5 * 4 * 3) * (5 * 4) --------------------- 10 * 9 * 8 * 7 * 6Now, from here we can see a pattern. The bottom is always going to decrease by one from (2*n) to (n+1). This product is equal to (2*n)! / (n!). On the top, we are multiplying two products, one 5*4*3, the other 5*4. Again, see the pattern. We are decreasing by one from n to k+1, then again from n to n-k. This gives us n!/k! * n!/(n-k)!. This quotient will give us the odds of picking k red balls in a row, then picking n-k white balls in a row, giving us a total of n balls from a sample of 2n marbles.
n! n!
-- * ------
k! (n-k)! (n!)^3
----------- = -------------
(2n)! k!(n-k)!(2n)!
-----
n!
However, we are only taking the odds of choosing the red balls right in a row, then choosing the white balls. We need to multiply this result by the number of possible ways of drawing k red and n-k white marbles. This product is simply nCk, or n!/((n-k)!k!) (you can enter binomial(n,k) in Maple). Taking the product of these two gives us the answer above.
n! n!
-- * ------
k! (n-k)! n! (n!)^4
----------- * -------- = ---------------------
(2n)! (n-k)!k! (k!)^2((n-k)!)^2(2n)!
-----
n!