Hints and solutions to
Try a Simpler Version #1

How many line segments can be drawn through each pair of 15 points? No
three points are in a straight line.
- This week the solution strategy is to "simplify the problem".
In other words, for these problems it is often helpful to consider
simpler or smaller cases
of the problem being asked. Today's problem is a good example.
-
We could immediately try and draw the
complete diagram:

Clearly, it will be too hard to count all the line segments in this
diagram!
- So, we should try and simplify the problem. What happens if we take
only three or four points?
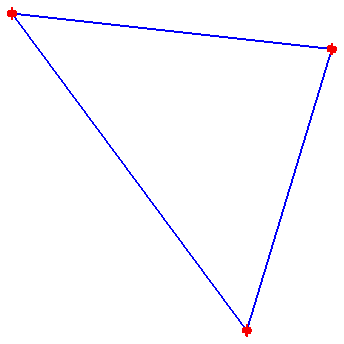
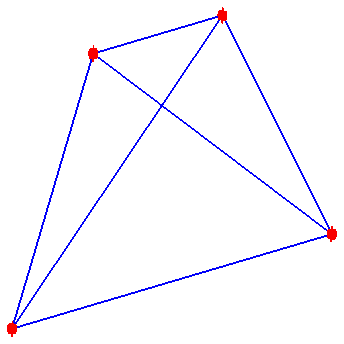
In these small cases, the number of segments is easy to count.
- We could begin to make a systematic list:
pointssegments
10
21
33
46
510
and so forth. You might recognize these as "triangular numbers", or
you might notice the pattern that to get the number of segments between
n+1
points, you add n to the number of segments for n points.
-
Using this last observation, you can see that the number of
segments for n points is 1 + 2 + 3 + ... + (n-1).
- This observation can be reinforced by realizing that the process
of drawing the segments can be organized as follows: Pick one point, and
start by drawing all the segments from that point to all the other
points.
If there are n points altogether, then there are n-1
"other"
points, so you draw n-1 segments. Then choose a second point, and
draw all segments from there. Since the segment back to the first point
is already drawn, you will only draw n-2 new segments. And so
forth.
This generates the answer as a sum, as noted above.
-
A little more thought in this direction gives the answer even more
directly (and gives the familiar formula for the sum of the first
n-1
numbers as a bonus): If there are n points, then there are
n-1
segments drawn starting at each point. This sounds like there should be
n(n-1) segments altogether, but observe that since every
segment
connects two points, you have counted each segment twice in this process.
- Therefore, the total number of segments connecting n points
is
n(n-1)/2 (which is also the value of the sum 1 + 2 + 3 +
... +
(n-1)).
- In particular, for 15 points, there are
15(14)/2 = 105 segments.
- This week the solution strategy is to "simplify the problem". In other words, for these problems it is often helpful to consider simpler or smaller cases of the problem being asked. Today's problem is a good example.
-
We could immediately try and draw the
complete diagram:

Clearly, it will be too hard to count all the line segments in this diagram!
- So, we should try and simplify the problem. What happens if we take
only three or four points?


In these small cases, the number of segments is easy to count.
- We could begin to make a systematic list:
points
segments
1
0
2
1
3
3
4
6
5
10
and so forth. You might recognize these as "triangular numbers", or you might notice the pattern that to get the number of segments between n+1 points, you add n to the number of segments for n points.
- Using this last observation, you can see that the number of segments for n points is 1 + 2 + 3 + ... + (n-1).
- This observation can be reinforced by realizing that the process of drawing the segments can be organized as follows: Pick one point, and start by drawing all the segments from that point to all the other points. If there are n points altogether, then there are n-1 "other" points, so you draw n-1 segments. Then choose a second point, and draw all segments from there. Since the segment back to the first point is already drawn, you will only draw n-2 new segments. And so forth. This generates the answer as a sum, as noted above.
- A little more thought in this direction gives the answer even more directly (and gives the familiar formula for the sum of the first n-1 numbers as a bonus): If there are n points, then there are n-1 segments drawn starting at each point. This sounds like there should be n(n-1) segments altogether, but observe that since every segment connects two points, you have counted each segment twice in this process.
- Therefore, the total number of segments connecting n points is n(n-1)/2 (which is also the value of the sum 1 + 2 + 3 + ... + (n-1)).
- In particular, for 15 points, there are 15(14)/2 = 105 segments.