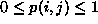 for all i and j and
for all i and j and
Recall that at the end of the last lecture we had started to discuss joint probability functions of two (or more) random variables. With two random variables X and Y, we define joint probability functions as follows:
For discrete variables, we let p(i,j) be the probability that X=i and Y=j.
This give a function p, called the joint probability function of X and Y that
is defined on (some subset of) the set of pairs of integers and such that
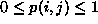 for all i and j and
for all i and j and
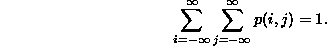
When we find it convenient to do so, we will set p(i,j)=0 for all i and j outside the domain we are considering.
For continuous variables, we define the joint probability density function p(x,y) on (some subset of) the plane of pairs of real numbers. We interpret the function as follows: p(x,y)dxdy is (approximately) the probability that X is between x and x+dx and Y is between y and y+dy (with error that goes to zero faster than dx and dy as they both go to zero). Thus, p(x,y) must be a non-negative valued function with the property that
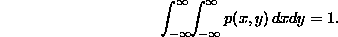
As with discrete variables, if our random variables always lie in some subset of the plane, we will define p(x,y) to be 0 for all (x,y) outside that subset.
We take one simple example of each kind of random variable. For the discrete random variable, we consider the roll of a pair of dice. We assume that we can tell the dice apart, so there are thirty-six possible outcomes and each is equally likely. Thus our joint probability function will be
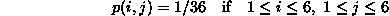
and p(i,j)=0 otherwise.
For our continuous example, we take the example mentioned at the end of the last lecture:

for (x,y) in the triangle with vertices (0,0), (2,0) and (2,2), and p(x,y)=0 otherwise. We checked last time that this is a probability density function (its integral is 1).
Often when confronted with the joint probability of two random variables, we wish to restrict our attention to the value of just one or the other. We can calculate the probability distribution of each variable separately in a straightforward way, if we simply remember how to interpret probability functions. These separated probability distributions are called the marginal distributions of the respective individual random variables.
Given the joint probability function p(i,j) of the discrete variables X and
Y, we will show how to calculate the marginal distributions 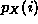 of X
and
of X
and  of Y. To calculate
of Y. To calculate 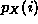 , we recall that
, we recall that 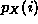 is the
probability that X=i. It is certainly equal to the probability that X=i and
Y=0, or X=i and Y=1, or .... In other words the event X=i is the union of
the events X=i and Y=j as j runs over all possible values. Since these
events are disjoint, the probability of their union is the sum of the
probabilities of the events (namely, the sum of p(i,j)). Thus:
is the
probability that X=i. It is certainly equal to the probability that X=i and
Y=0, or X=i and Y=1, or .... In other words the event X=i is the union of
the events X=i and Y=j as j runs over all possible values. Since these
events are disjoint, the probability of their union is the sum of the
probabilities of the events (namely, the sum of p(i,j)). Thus:

Likewise,
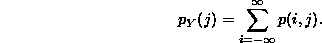
Make sure you understand the reasoning behind these two formulas!
An example of the use of this formula is provided by the roll of two dice discussed above. Each of the 36 possible rolls has probability 1/36 of occurring, so we have probability function p(i,j) as indicated in the following table:

The marginal probability distributions are given in the last column and last row of the table. They are the probabilities for the outcomes of the first (resp second) of the dice, and are obtained either by common sense or by adding across the rows (resp down the columns).
For continuous random variables, the situation is similar. Given the joint
probability density function p(x,y) of a bivariate distribution of the two
random variables X and Y (where p(x,y) is positive on the actual sample
space subset of the plane, and zero outside it), we wish to calculate the
marginal probability density functions of X and Y. To do this, recall that
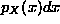 is (approximately) the probability that X is between x and
x+dx. So to calculate this probability, we should sum all the probabilities
that both X is in [x,x+dx] and Y is in [y,y+dy] over all possible values of Y.
In the limit as dy approaches zero,this becomes an integral:
is (approximately) the probability that X is between x and
x+dx. So to calculate this probability, we should sum all the probabilities
that both X is in [x,x+dx] and Y is in [y,y+dy] over all possible values of Y.
In the limit as dy approaches zero,this becomes an integral:
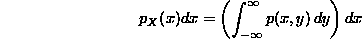
In other words,
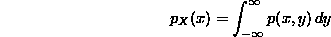
Similarly,
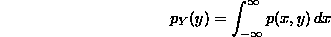
Again, you should make sure you understand the intuition and the reasoning behind these important formulas.
We return to our example:

for (x,y) in the triangle
with
vertices (0,0), (2,0) and (2,2), and p(x,y)=0 otherwise, and compute its
marginal density functions. The easy one is 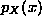 so we do that one
first. Note that for a given value of x between 0 and 2, y ranges from 0 to
x inside the triangle:
so we do that one
first. Note that for a given value of x between 0 and 2, y ranges from 0 to
x inside the triangle:
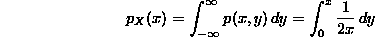

if  , and
, and 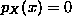 otherwise. This indicates that the values
of X are uniformly distributed over the interval from 0 to 2 (this agrees
with the intuition that the random points occur with greater density
toward the left side of the triangle but there is more area on the right
side to balance this out).
otherwise. This indicates that the values
of X are uniformly distributed over the interval from 0 to 2 (this agrees
with the intuition that the random points occur with greater density
toward the left side of the triangle but there is more area on the right
side to balance this out).
To calculate 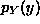 , we begin with the observation that for each value
of y between 0 and 2, x ranges from y to 2 inside the triangle:
, we begin with the observation that for each value
of y between 0 and 2, x ranges from y to 2 inside the triangle:
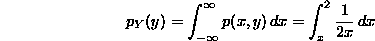
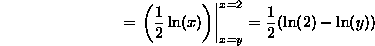
if 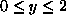 and
and 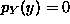 otherwise. Note that
otherwise. Note that 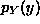 approaches
infinity as y approaches 0 from above, and
approaches
infinity as y approaches 0 from above, and 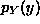 approaches 0 as y
approaches 2. You should check that this function is actually a probability
density function on the interval [0,2], i.e., that its integral is 1.
approaches 0 as y
approaches 2. You should check that this function is actually a probability
density function on the interval [0,2], i.e., that its integral is 1.
Frequently, it is necessary to calculate the probability (density) function of a function of two random variables, given the joint probability (density) function. By far, the most common such function is the sum of two random variables, but the idea of the calculation applies in principle to any function of two (or more!) random variables.
The principle we will follow for discrete random variables is as follows:
to calculate the probability function for F(X,Y), we consider the events
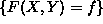 for each value of f that can result from evaluating F at
points of the sample space of (X,Y). Since there are only countably many
points in the sample space, the random variable F that results is discrete.
Then the probability function
for each value of f that can result from evaluating F at
points of the sample space of (X,Y). Since there are only countably many
points in the sample space, the random variable F that results is discrete.
Then the probability function 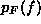 is
is
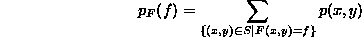
This seems like a pretty weak principle, but it is surprisingly useful when combined with a little insight (and cleverness).
As an example, we calculate the distribution of the sum of the two dice. Since the outcome of each of the dice is a number between 1 and 6, the outcome of the sum must be a number between 2 and 12. So for each f between 2 and 12:
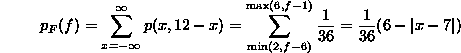
A table of the probabilities of various sums is as follows:
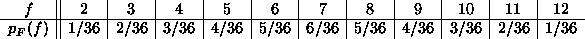
The "tent-shaped" distribution that results is typical of the sum of (independent) uniformly distributed random variables.
For continuous distributions, our principle will be a little more
complicated, but more powerful as well. To enunciate it, we recall that to
calculate the probability of the event F<f, we integrate the pdf of F
from 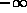 to f:
to f:

Conversely, to recover the pdf of F, we can differentiate the resulting function:
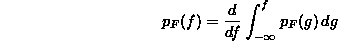
(this is simply the
first fundamental theorem of calculus). Our principle for calculating the
pdf of a function of two random variables F(X,Y) will be to calculate the
probabilities of the events 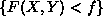 (by integrating the joint pdf over
the region of the plane defined by this inequality), and then to
differentiate with respect to f to get the pdf.
(by integrating the joint pdf over
the region of the plane defined by this inequality), and then to
differentiate with respect to f to get the pdf.
We apply this principle to calculate the pdf of the sum of the random variables X and Y in our example:

for (x,y) in the
triangle T with
vertices (0,0), (2,0) and (2,2), and p(x,y)=0 otherwise. Let Z=X+Y. To
calculate the pdf 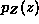 , we first note that for any fixed number z, the
region of the plane where Z<z is the half plane below and to the left of
the line y=z-x. To calculate the probability
, we first note that for any fixed number z, the
region of the plane where Z<z is the half plane below and to the left of
the line y=z-x. To calculate the probability 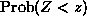 , we must
integrate the joint pdf p(x,y) over this region. Of course, for
, we must
integrate the joint pdf p(x,y) over this region. Of course, for 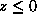 , we
get zero since the half plane z<0 has no points in common with the
triangle where the pdf is supported. Likewise, since both X and Y are
always between 0 and 2 the biggest the sum can be is 4. Therefore
, we
get zero since the half plane z<0 has no points in common with the
triangle where the pdf is supported. Likewise, since both X and Y are
always between 0 and 2 the biggest the sum can be is 4. Therefore
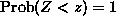 for all
for all  .
.
For z between 0 and 4, we need to integrate 1/2x over the intersection of
the half-plane x+y<z and the triangle T. The shape of this intersection is
different, depending upon whether z is greater than or less than 2: If 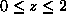 , the intersection is a triangle with vertices at the points (0,0),
(z/2,z/2) and (z,0). In this case, it is easier to integrate first with
respect to x and then with respect to y, and we can calculate:
, the intersection is a triangle with vertices at the points (0,0),
(z/2,z/2) and (z,0). In this case, it is easier to integrate first with
respect to x and then with respect to y, and we can calculate:
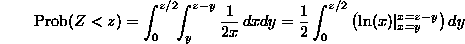
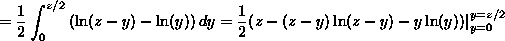

And since the (cumulative) probability that Z<z is 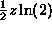 for 0<z<2, the pdf over this range is
for 0<z<2, the pdf over this range is 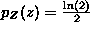 .
.
The calculation of the pdf for 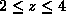 is somewhat trickier because
the intersection of the half-plane x+y<z and the triangle T is more
complicated. The intersection in this case is a quadrilateral with vertices
at the points (0,0), (z/2,z/2), (2,z-2) and (2,0). We could calculate
is somewhat trickier because
the intersection of the half-plane x+y<z and the triangle T is more
complicated. The intersection in this case is a quadrilateral with vertices
at the points (0,0), (z/2,z/2), (2,z-2) and (2,0). We could calculate
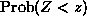 by integrating p(x,y) over this quadrilateral. But we will be a
little more clever: Note that the quadrilateral is the "difference" of two
sets. It consists of points inside the triangle with vertices (0,0),
(z/2,z/2), (z,0) that are to the left of the line x=2. In other words it is
points inside this large triangle (and note that we already have computed
the integral of 1/2x over this large triangle to be
by integrating p(x,y) over this quadrilateral. But we will be a
little more clever: Note that the quadrilateral is the "difference" of two
sets. It consists of points inside the triangle with vertices (0,0),
(z/2,z/2), (z,0) that are to the left of the line x=2. In other words it is
points inside this large triangle (and note that we already have computed
the integral of 1/2x over this large triangle to be 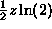 )
that are not inside the triangle with vertices (2,0), (2,z-2) and (z,0).
Thus, for
)
that are not inside the triangle with vertices (2,0), (2,z-2) and (z,0).
Thus, for 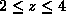 , we can calculate
, we can calculate 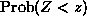 as
as
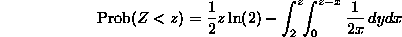
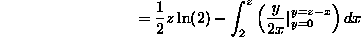
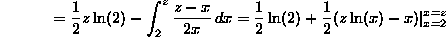
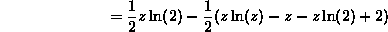
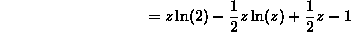
To get the pdf for 2<z<4, we need only differentiate this quantity, to get
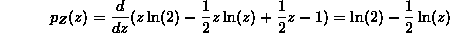
Now we have the pdf of Z = X+Y for all values of z. It is 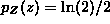 for 0<z<2, it is
for 0<z<2, it is 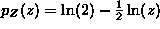 for 2<z<4 and it is 0
otherwise. It would be good practice to check that the integral of
for 2<z<4 and it is 0
otherwise. It would be good practice to check that the integral of 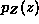 is 1.
is 1.
In our study of stochastic processes, we will often be presented with
situations where we have some knowledge that will affect the probability
of whether some event will occur. For example, in the roll of two dice,
suppose we already know that the sum will be greater than 7. This changes
the probabilities from those that we computed above. The event 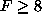 has probability (5+4+3+2+1)/36=15/36. So we are restricted to less than
half of the original sample space. We might wish to calculate the
probability of getting a 9 under these conditions. The quantity we wish to
calculate is denoted
has probability (5+4+3+2+1)/36=15/36. So we are restricted to less than
half of the original sample space. We might wish to calculate the
probability of getting a 9 under these conditions. The quantity we wish to
calculate is denoted  , read "the probability that
F=9 given that
, read "the probability that
F=9 given that 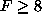 ".
".
In general to calculate 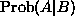 for two events A and B (it is not
necessary that A is a subset of B), we need only realize that we need to
compute the fraction of the time that the event B is true, it is also the
case the A is true. In symbols, we have
for two events A and B (it is not
necessary that A is a subset of B), we need only realize that we need to
compute the fraction of the time that the event B is true, it is also the
case the A is true. In symbols, we have

For our dice example (noting that the event F=9 is a subset of the event
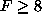 ), we get
), we get
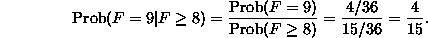
As another example (with continuous probability this time), we calculate
for our 1/2x on the triangle example the conditional probabilities:
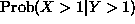 as well as
as well as 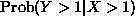 (just to show
that the probabilities of A given B and B given A are usually different).
(just to show
that the probabilities of A given B and B given A are usually different).
First 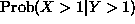 . This one is easy! Note that in the triangle
with vertices (0,0), (2,0) and (2,2) it is true that Y>1 implies that
X>1. Therefore the events
. This one is easy! Note that in the triangle
with vertices (0,0), (2,0) and (2,2) it is true that Y>1 implies that
X>1. Therefore the events 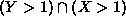 and Y>1 are the same, so
the fraction we need to compute will have the same numerator and
denominator. Thus
and Y>1 are the same, so
the fraction we need to compute will have the same numerator and
denominator. Thus 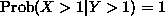 .
.
For 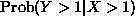 we actually need to compute something. But
note that Y>1 is a subset of the event X>1 in the triangle, so we get:
we actually need to compute something. But
note that Y>1 is a subset of the event X>1 in the triangle, so we get:
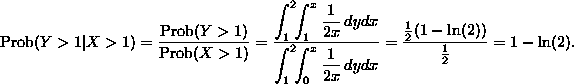
Two events A and B are called independent if the probability of A given B is the same as the probability of A (with no knowledge of B) and vice versa. The assumption of independence of certain events is essential to many probabilistic arguments. Independence of two random variables is expressed by the equations:
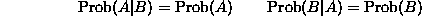
and especially

Two random variables X and Y are independent if the probability that a<X<b remains unaffected by knowledge of the value of Y and vice versa. This reduces to the fact that the joint probability (or probability density) function of X and Y "splits" as a product:

of the marginal probabilities (or probability densities). This formula is a straightforward consequence of the definition of independence and is left as an exercise.
1. Let p(x,y) be the uniform joint probability density on the unit disk, i.e.,
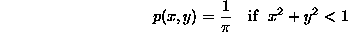
and p(x,y)=0 otherwise. Calculate the pdf of X+Y. Also find the expected value and variance of X+Y.
2. Suppose X and Y are independent random variables, each distributed
according to the exponential distribution with parameter 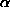 . Find
the joint pdf of X and Y (easy). Find the pdf of X+Y. Also find the mean and
variance of X+Y.
. Find
the joint pdf of X and Y (easy). Find the pdf of X+Y. Also find the mean and
variance of X+Y.
3. Prove that two random variables are independent if and only if their joint probability (density) function is the product of the marginal probability (density) functions.