2. (corresponds somewhat to the binomial distribution). The Normal Distribution (or Gaussian distribution). This is the most important probability distribution, because the distribution of the average of the results of repeated experiments always approaches a normal distribution (this is the "law of large numbers"). The sample space for the normal distribution is always the entire real line. But to begin, we need to calculate an integral: 
We will use a trick that goes back (at least) to Liouville: First, note that



because we can certainly change the name of the variable in the second integral, and then we can convert the product of single integrals into a double integral. Now (the critical step), we'll evaluate the integral in polar coordinates (!!) -- note that over the whole plane, r goes from 0 to infinity as  goes from 0 to
goes from 0 to 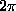 , and dxdy becomes
, and dxdy becomes 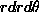 :
:

Therefore, I=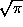 . We need to arrange things so that the integral is 1, and for reasons that will become apparent later, we arrange this as follows: define
. We need to arrange things so that the integral is 1, and for reasons that will become apparent later, we arrange this as follows: define

Then N(x) defines a probability distribution, called the standard normal distribution. Here is a graph of N(x):

More generally, we define the normal distribution with parameters 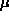 and
and  to be
to be
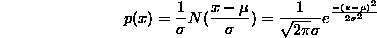
Expectation of a Random Variable
The expectation of a random variable is essentially the average value it is expected to take on. Therefore, it is calculated as the weighted average of the possible outcomes of the random variable, where the weights are just the probabilities of the outcomes. As a trivial example, consider the (discrete) random variable X (outcomes of some probabilistic experiment) whose sample space is the set {1,2,3} with probability function given by p(1)=0.3, p(2)=0.1 and p(3)=0.6. If we repeated this experiment 100 times, we would expect to get about 30 occurrences of X=1, 10 of X=2 and 60 of X=3. The average X would then be ((30)(1)+(10)(2)+(60)(3))/100 = 2.3. In other words, (1)(0.3)+(2)(0.1)+(3)(0.6). This reasoning leads to the defining formula:

for any discrete random variable. The notation E(X) for the expectation of X is standard, also in use is the notation 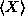 .
.
For continuous random variables, the situation is similar, except the sum is replaced by an integral (think of summing up the average values of x by dividing the sample space into small intervals [x,x+dx] and calculating the probability p(x)dx that X falls into the interval. By reasoning similar to the previous paragraph, the expectation should be
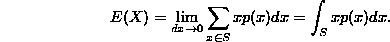
This is the formula for the expectation of a continuous random variable.
Examples:
- 1. Uniform discrete: We'll need to use the formula for
 that you learned in freshman calculus when you evaluated Riemann sums:
that you learned in freshman calculus when you evaluated Riemann sums:

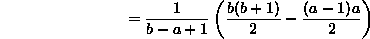

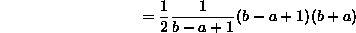

which is what we should have expected from the uniform distribution.
- 2. Uniform continuous: (We expect to get (b+a)/2 again, right?). This is easier:
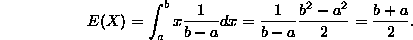
- 3. Poisson distribution with parameter
 : Before we do this, recall the Taylor series formula for the exponential function:
: Before we do this, recall the Taylor series formula for the exponential function: 
Note that we can take the derivative of both sides to get the formula:

If we multiply both sides of this formula by x we get

We will use this formula with x replaced by  .
.
If X is a discrete random variable with a Poisson distribution, then its expectation is:
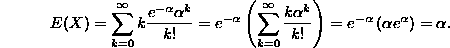
- 4. Exponential distribution with parameter
 . This is a little like the Poisson calculation (with improper integrals instead of series), and we will have to integrate by parts (we'll use u=x so du=dx, and dv=
. This is a little like the Poisson calculation (with improper integrals instead of series), and we will have to integrate by parts (we'll use u=x so du=dx, and dv=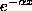 dx so that v will be
dx so that v will be  ):
):

Note the difference between the expectations of the Poisson and exponential distributions!!
By the symmetry of the respective distributions around their "centers", it is pretty easy to conclude that the expectation of the binomial distribution (with parameter n) is n/2, and the expectation of the normal distribution (with parameters 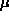 and
and  ) is
) is 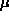 .
.
Homework problems:
- Make your own example of a probability space that is finite and discrete. Calculate the expectation of the underlying random variable X.
- Make your own example of a probability space that is infinite and discrete. Calculate the expectation of the underlying random variable X.
- Make your own example of a continuous random variable. Calculate its expectation.
- Prove that the normal distribution function

is really a probability density function on the real line (i.e., that it is positive and that its integral from -infinity to infinity is 1). Calculate the expectation of this random variable.
- What is the relationship among the following partial derivatives?
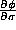 ,
,  , and
, and 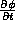 , where
, where 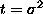 (for the last one, rewrite
(for the last one, rewrite 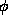 as a function of x,
as a function of x, 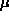 and t).
and t).
- Consider the experiment of picking a point at random from a uniform distribution on the disk of radius R centered at the origin in the plane ("uniform" here means if two regions of the disk have the same area, then the random point is equally likely to be in either one). Calculate the probability density function and the expectation of the random variable D, defined to be the distance of the random point from the origin.
Dennis DeTurck
Mon May 27 13:57:15 EDT 1996
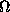 of subsets of S (so
of subsets of S (so 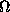 itself is a subset of the power set
itself is a subset of the power set 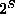 of all subsets of S) that contains the empty set, contains S itself, and is closed under finite intersections and countable unions. When the basic set S is finite (or countably infinite), then
of all subsets of S) that contains the empty set, contains S itself, and is closed under finite intersections and countable unions. When the basic set S is finite (or countably infinite), then 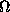 is taken to be all subsets of S. When S is a continuous subset of the real line, this is not possible, and one usually restricts attention to the set of subsets that can be obtained by starting with all open intervals and taking intersections and unions (countable) of them -- the so-called Borel sets [or more generally, Lebesgue measurable subsets of S].
is taken to be all subsets of S. When S is a continuous subset of the real line, this is not possible, and one usually restricts attention to the set of subsets that can be obtained by starting with all open intervals and taking intersections and unions (countable) of them -- the so-called Borel sets [or more generally, Lebesgue measurable subsets of S]. 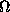 is the collection of sets to which we will assign probabilities.
is the collection of sets to which we will assign probabilities.
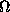 to the real numbers that assigns probabilities to events. The function p must have the properties that:
to the real numbers that assigns probabilities to events. The function p must have the properties that:
 )=0.
)=0.
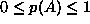 for every
for every 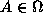
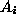 , i=1,2,3,.... is a countable (finite or infinite) collection of disjoint sets (i.e.,
, i=1,2,3,.... is a countable (finite or infinite) collection of disjoint sets (i.e., 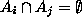 for all i different from j), then
for all i different from j), then 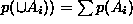 .
.
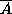 is the complement of A, then p(
is the complement of A, then p(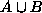 )=p(A)+p(B)-p(
)=p(A)+p(B)-p(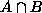 ), even if A and B are not disjoint.
), even if A and B are not disjoint.


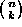 is the binomial coefficient
is the binomial coefficient 
 ) -- this arises as the number of (random) events of some kind (such as people lining up at a bank, or Geiger-counter clicks, or telephone calls arriving) per unit time. The sample space S is the set of all nonnegative integers S=0,1,2,3,...., and again
) -- this arises as the number of (random) events of some kind (such as people lining up at a bank, or Geiger-counter clicks, or telephone calls arriving) per unit time. The sample space S is the set of all nonnegative integers S=0,1,2,3,...., and again 




 (or we can just let p(x)=0 for x<0). The probability function is given by
(or we can just let p(x)=0 for x<0). The probability function is given by 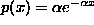 . It is easy to check that the integral of p(x) from 0 to infinity is equal to 1, so p(x) defines a bona fide probability density function. Here are graphs of exponential distribution functions with parameters 1, 1.5 and 2:
. It is easy to check that the integral of p(x) from 0 to infinity is equal to 1, so p(x) defines a bona fide probability density function. Here are graphs of exponential distribution functions with parameters 1, 1.5 and 2:





 goes from 0 to
goes from 0 to 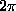 , and dxdy becomes
, and dxdy becomes 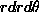 :
:

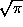 . We need to arrange things so that the integral is 1, and for reasons that will become apparent later, we arrange this as follows: define
. We need to arrange things so that the integral is 1, and for reasons that will become apparent later, we arrange this as follows: define 

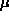 and
and  to be
to be 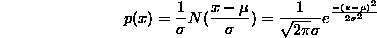

 .
.
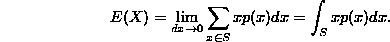
 that you learned in freshman calculus when you evaluated Riemann sums:
that you learned in freshman calculus when you evaluated Riemann sums:

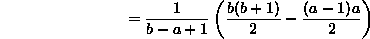

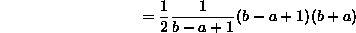

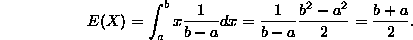



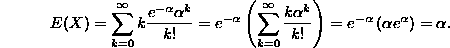
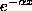 dx so that v will be
dx so that v will be  ):
):


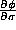 ,
,  , and
, and 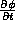 , where
, where 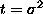 (for the last one, rewrite
(for the last one, rewrite 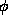 as a function of x,
as a function of x,