Middle School Problems of the Day
Week 7 hints and answers
As always, these hints and answers are intended to promote and provoke
class
discussions. The answers that are posted for students to read on
the website a few days after each problem is posted are based in
the answers that appear here.
ANSWERS TO THIS WEEK'S PROBLEMS
1. Determine the number of integers between 1 and 1000 that contain
at least one 2 but no 3.
- Before turning the students loose on this one, it might be
good to review the multiplication principle for counting things,
as well as the "at least one" principle (that it's easier to
count how many contain "none", and subtract this from the total
amount).
- What pattern shall we look for? Let's try doing the problem for
numbers between 1 and 10, then between 1 and 100.
- There are 10 numbers between 1 and 10. Only one of them contains
a 2 (namely, 2 itself), and there's no 3 here.
- There are 100 numbers between 1 and 100 - Let's list all of the
ones that have a digit "2" -- 2, 12, 20, 21, 22, 23, 24, 25, 26, 27, 28,
29, 32, 42, 52, 62, 72, 82, 92. There are 19 numbers here, but two
of them have "3"s. So there are 17 numbers between 1 and 100 that contain
at least one 2 but no 3.
- Let's think about how to do this without writing all the numbers
down. We certainly don't want to have to do that for 1 to 1000!
- How many numbers between 1 and 100 have no 3 in them? If we're
not allowing any 3's then there are 9 ways to pick the tens digit
and 9 ways to pick the ones digit (we're allowing numbers like 03 for
3 etc). So there are 81 numbers between 1 and 100 with no 3's.
- Next, let's figure out how many of these have at least one 2.
Actually, it's easier to do the opposite -- to figure out how many of
the 81 numbers with no 3's have no 2's either. Then we can subtract
this number from 81 to get the number of numbers with no 3's that have at
least one 2.
- So, how many numbers between 1 and 100 have no 2's and no 3's? Now
there are 8 ways to pick the tens digit and 8 ways to pick the ones
digit, which gives us 64. So we're not interested in 64 of
the 81 numbers with no 3's -- this leaves 17 that have at least one
2 but no 3's, just as we calculated above. Notice, this is 92 - 82.
- Now
we're ready to tackle the numbers from 1 to 1000.
- How many numbers from 1 to 1000 have at least no 3's in them?
Just as for the 1 to 100 case, we have 9 ways to pick the hundreds digit,
9 ways to pick the tens digit and 9 ways to pick the ones digit. This
makes 93 = 729 numbers with no 3s.
- Now we want to "throw away" the ones that don't have any 2's either.
Again as before, there are 8x8x8 of these (since there are now 8 ways to
pick the hundreds digit, 8 to pick the tens and 8 to pick the ones).
- So we're left with 93 - 83 = 729-512 = 217
numbers with at least one 2 but no 3's.
- You might want to try numbers from 1 to 10,000 next.
2. How many numbers less than 124 are divisible by 2, 3 and 5?
- Well, since 2 x 62 = 124, there are 62 multiples of 2.
And 124 = 3 x 41 + 1, so there are 41 multiples of 3 less than 124,
and 124 = 5 x 24 + 4, so there are 24 multiples of 5 less than 124.
- But it might be easier to think about which numbers are multiples of
all three of 2, 3 and 5. (To do a simpler one, you might consider which
numbers are multiples of both 2 and 3, or 2 and 5, or 3 and 5).
- If a number is divisible by all three of 2, 3, and 5, then it must be
divisible by their product (since they are all prime numbers). Thus,
it is the multiples of 2 x 3 x 5 = 30 that are divisible by all three.
- And there are 4 multiples of 30 less than 124, so the answer to this question
is 4.
3. Can you find a number that fits this pattern? 3600 , 1800, 600, 150, __?__
- Looks like everybody is a multiple of 150 here, so let's look for a
multiplicative pattern.
- To get from 3600 to 1800, you divide by 2.
- To get from 1800 to 600, you divide by 3.
- And to get from 600 to 150, you divide by 4.
- So one way to finish the pattern is to divide 150 by 5, and get that
the next number is 30.
4. If you added 6 rows to the bottom of this picture, how many small triangles
would you have altogether?
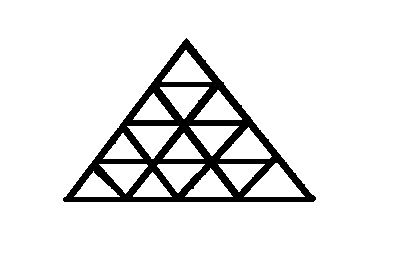
- Well, you could draw the picture and try and count all the triangles,
but it might be better to look for a pattern.
- We're only counting little triangles here, so let's start by
counting how many are in each row.
- Looks like there is 1 triangle in the top row, then 3 in the second row,
5 in the third, and so forth.
- In the picture so far, there are 1 + 3 + 5 + 7 triangles. This is the sum
of the first four odd numbers and remember back to the very first POD, this
is 42=16.
- So if we add six more rows, we'll have the sum of the first 10 odd numbers,
so the total number of small triangles will be 102 = 100.
5. 2010 - 2000 + 1990 - 1980 + 1970 - 1960 + ..... - 20 + 10 = ?