Middle School Problems of the Day

Week 28 hints and answers

As always, these hints and answers are intended to promote and provoke class discussions. The answers that are posted for students to read on the website a few days after each problem is posted are based in the answers that appear here.

ANSWERS TO THIS WEEK'S PROBLEMS

1. What is the perimeter of a square with a diagonal of 36?

A picture will definitely help you solve this problem!
If the diagonal of a square is 36, then each side must be 36 divided by the square root of 2 (because two sides and a diagonal form a right-angle triangle, and so the Pythagorean theorem says side² + side² = diagonal², and since the sides are the same in a square, you get 2 side² = diagonal²).
Now we can get the perimiter of the square by multiplying the side length by 4 - so the perimeter is 144 divided by the square root of 2, or about 101.8.

2. Determine the largest number of boxes of dimensions 2x2x3 that can be placed inside a box 3x4x5.

Another one for a picture! You might also try building a model! Also consider simplifying the problem by considering a few two-dimensional versions.
If you just consider the volumes of the boxes, a 2x2x3 box has volume 12 cubic units, and a 3x4x5 box has volume 60 cubic units. So we certainly cannot put more than 5 small boxes into the large one. But do the shapes of the boxes allow for this possibility?
Thinking from the other direction, we can certainly get four 2x2x3 boxes into the big box, by putting the "3" side of the little box along the "3"side of the large one. Imagine the big box with the tall (5) side vertical, and its 3 and 4 sides on the floor. You can then place two 2x2x3 boxes side by side in the bottom of the big box, and then make another layer of two 2x2x3 boxes, like this:
In this way, you'll have filled 3x4x4 of the big box, but there won't be any more room for little boxes, since the remaining height is only 1 unit, but all the dimensions of the little boxes are at least two units.
Another way to get four little boxes into the big box is to start with two side-by-side on the bottom as before, but then put the other two in with their 2x2 side down, as shown here:
So the answer is either 4 or 5. How can we show that it isn't 5? Well, since the shortest dimension of the big box is 3, and the shortest dimension of the little boxes is 2, you can't put a "2" side of a little box along the 3 side of the big box, or else you'll end up with a space that's only 1 unit wide, into which you can't put a little box, no matter which way you turn it.
So you have to start as we did above, with two boxes side-by-side on the bottom. But then you have the same problem on the second level, so you can't get away without wasting some space. That means that 5 little boxes won't fit, so you can get at most 4 little boxes into the big one.

3. A (regular) hexagon is inscribed in a circle, which is inscribed in a square of side 10 cm. What is the length of each side of the hexagon?

I guess you can tell that this is the week for picture problems!
Since the sides of the square are 10 cm long, the radius of the circle is 5 cm. If you draw two radii from the center of the circle to adjacent corners of the hexagon as follows:
then there is a triangle formed, with two black sides (the radii), and one green side (a side of the hexagon).
The two black sides of the triangle, being radii of the circle, are each 5 cm long. And the angle between them is 60 degrees, because there are six such angles around the center of the circle, and 1/6 of 360 degrees is 60 degrees.
So our triangle is isosceles and has a 60 degree angle between its two equal sides.
But the angles opposite the equal sides of an isosceles triangle must also be equal - and the three angles of the triangle add up to 180 degrees. That means these two angles must also be 60 degrees. So our triangle is not just isosceles, it is equilateral. So all three of its sides are 5 cm long.
But the green side of the triangle is a side of the hexagon - so each side of the hexagon is 5 cm long.

4. A golf ball falls randomly into a circular green 10 meters in radius, with the cup at the center. What is the probability that the ball falls within 1 meter of the cup?

This is a probability/geometry problem -- we need to know what fraction of the area of the green is within 1 meter of the cup.
The area of the entire green is pi(10²) = 100pi square meters, and the area of the cup is only pi(1²) = pi square meters.
So the probability of being within 1 meter of the cup is only pi/(100pi) = 1/100 = 0.01.

5. Three vertices of a parallelogram are ( 1, 1), ( 3, 5 ), and ( -1, 4 ). Find all possible ordered pairs that could be the coordinates of the fourth vertex.

It is perhaps surprising that there is more than one possible answer to this problem. From the picture you can see that there are in fact three answers. Can you find all of them?
Let's start by connecting the three points in each of the three possible ways (two must be on the ends and one in the middle - and there are three of them that can be in the middle):
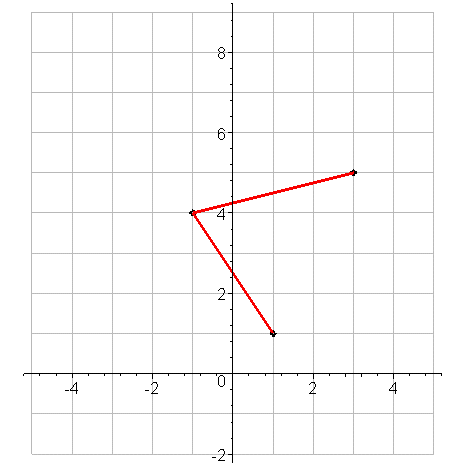
In the first picture, we can complete the parallelogram by starting at the (1,1) vertex and going one unit up and 4 units to the right (just as the top edge does). That gives us the following picture:
And you can see that the fourth vertex in this picture is (5,2).
In the second picture, we can complete the parallelogram by starting at the left vertex (-1,4), and going 4 units up and 2 to the right (just as the right edge does). That gives us the following picture:
And you can see that the fourth vertex in this picture is (1,8).
In the third picture, we can complete the parallelogram by starting at the bottom vertex (1,1) and going one unit down and four units to the left (as the top edge does). This gives us the following picture:
And you can see that the fourth vertex in this picture is (0,-3).
So the three points that can be the ordered pair of the fourth vertex of the parallelogram are (5,2), (1,8), (0,-3).