Hints and solutions to Problem of the day for Friday, May 8






Determine the largest number of boxes of dimensions 2x2x3 that can be
placed inside a box 3x4x5.
-
Another one for a picture! You might also try building a model! Also
consider simplifying the problem by considering a few two-dimensional
versions.
-
If you just consider the volumes of the boxes, a 2x2x3 box has volume
12
cubic units, and a 3x4x5 box has volume 60 cubic units. So we certainly
cannot
put more than 5 small boxes into the large one. But do the shapes of the
boxes allow for this possibility?
-
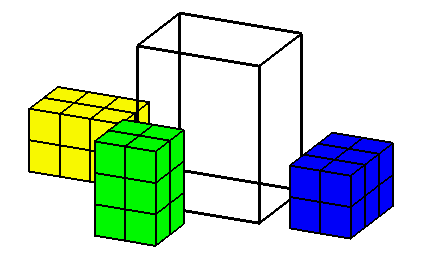
Thinking from the other direction, we can certainly get four 2x2x3
boxes
into the big box, by putting the "3" side of the little box along the
"3"side of the large one. Imagine the big box with the tall (5) side
vertical,
and its 3 and 4 sides on the floor. You can then place two 2x2x3 boxes
side
by side in the bottom of the big box, and then make another layer of two
2x2x3
boxes, like this:

In this way, you'll have filled 3x4x4 of the big box, but there
won't
be any more room for little boxes, since the remaining height is only 1
unit,
but all the dimensions of the little boxes are at least two units.
-
Another way to get four little boxes into the big box is to start with
two side-by-side on the bottom as before, but then put the other two in
with their 2x2 side down, as shown here:

-
So the answer is either 4 or 5. How can we show that it isn't 5?
Well, since the shortest dimension of the big box is 3, and the shortest
dimension of the little boxes is 2, you can't put a "2" side of a little
box
along the 3 side of the big box, or else you'll end up with a space
that's only 1 unit wide, into which you can't put a little box, no matter
which way
you turn it.
-
So you have to start as we did above, with two boxes side-by-side on the
bottom.
But then you have the same problem on the second level, so you can't get
away
without wasting some space. That means that 5 little boxes won't fit, so
you
can get at most 4 little boxes into the big one.















