CHAPTER 8 - Infinite series
Section 8.1, page 619
Problems 35 and 36
We'll just calculate the limits:
| > | limit(1-1/n,n=infinity), limit(n-1/n,n=infinity); |
![]()
So the sequence in problem 35 converges to 1, and the one in problem 36 diverges.
Problem 55
| > | a:=n->n^(1/n); |
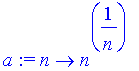
| > | seq([n,evalf(a(n))],n=1..25); |
![]()
![]()
![]()
![]()
![]()
![]()
Perhaps it's converging, let's see:
| > | limit(a(n),n=infinity); |
![]()
OK ... looks like we need to go pretty far out to get within 0.01:
| > | fsolve(a(n)=1.01,n=25..50000); |
![]()
So the error is not less than 0.01 until n=652. To get within 0.0001:
| > | fsolve(a(n)=1.0001,n=1000..500000); |
![]()
So we need 116,678 terms before we're within 0.0001.
Section 8.2, page 628
Problem 20
| > | limit((sin(n))^2/2^n,n=infinity); |
![]()
Problem 77
We want x = -cos(x). So we set
| > | g:=x->evalf(-cos(x)); |
![]()
and then start with, say x=0.
| > | g(0.0); |
![]()
| > | g(%); |
![]()
| > | g(%); |
![]()
| > | g(%); |
![]()
| > | g(%); |
![]()
| > | g(%); |
![]()
| > | g(%); |
![]()
| > | g(%); |
![]()
So we seem to be converging to about -0.72. Let's ask Maple:
| > | fsolve(x+cos(x)=0,x=-1..0); |
![]()
Section 8.3, page 638
Problem 39
| > | Sum((exp(1)/Pi)^n,n=0..infinity)=sum((exp(1)/Pi)^n,n=0..infinity); |
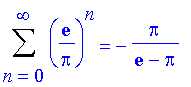
So this series converges.
Section 8.4, page 643
Problem 10
We'll integrate:
| > | int(ln(x)/sqrt(x),x=2..infinity); |
![]()
Since the integral diverges, so does the series.
Section 8.5, page 649
Problem 16
Since 1+ln(n)<![]() for large n, as can be seen from this graph:
for large n, as can be seen from this graph:
| > | plot({1+ln(n),sqrt(n)},n=1..20,color=blue,thickness=2); |
![[Maple Plot]](images/m104-ex826.gif)
| > | evalf(sqrt(20)),evalf(1+ln(20)); |
![]()
we see that 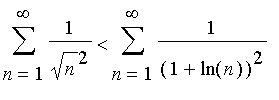 But
But
| > | int(1/n,n=1..infinity); |
![]()
So both series diverge.
Section 8.6, page 654
Problem 17
Ratio test:
| > | a:=n->(n+1)*(n+2)/n!; |
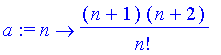
| > | limit(a(n+1)/a(n),n=infinity); |
![]()
So the series converges.
Section 8.7, page 661
Problem 26
Alternating series test:
| > | limit(1/(n*ln(n)),n=infinity); |
![]()
And the denominator is increasing, so the fraction is decreasing. So 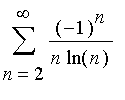 converges at least. To check absolute convergence, we'll use the integral test:
converges at least. To check absolute convergence, we'll use the integral test:
| > | int(1/(n*ln(n)),n=2..infinity); |
![]()
This diverges, so the original alternating series converges conditionally.
Section 8.8, page 671
Problem 17
First use the ratio test:
| > | a:=n->n*(x+3)^n/5^n; |
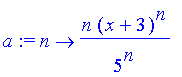
| > | limit(a(n+1)/a(n),n=infinity); |
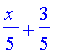
| > | solve(abs(%)<1,x); |
![]()
So the series converges for x between -8 and 2. What about the endpoints?
| > | simplify(subs(x=-8,a(n))); |
![]()
| > | simplify(subs(x=2,a(n))); |
![]()
Since these don't go to zero (nth term test), the series diverges for x=-8 and x=2. So the interval of convergence is (-8,2) -- the series converges absolutely for all those values of x.
Section 8.9, page 677
Problem 34
We'll find an expansion of higher order, just to show we can:
| > | taylor(exp(sin(x)),x=0,7); |
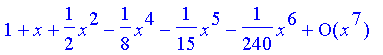
The linear approximation is thus 1+x, and the quadratic approximation is 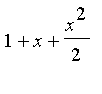 .
.
Section 8.10, page 686
Problem 21
If |x|<0.001, and since the Maclaurin series for sin(x):
| > | taylor(sin(x),x=0,8); |
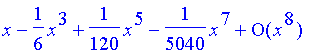
is alternating, the error is less than the first omitted term. So the error is less than
| > | 0.001/6; |
![]()
i.e., less than 0.00017.
Section 8.11, page 697
Problem 4
| > | taylor(sqrt(1+x),x=0,5); |
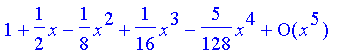
Problem 44
| > | taylor(Int(t^2*exp(-t^2),t=0..x),x=0,10); |
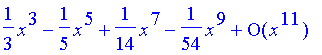
This is an alternating series, so to get error less than 0.001 for |x|<1, we need to find the first term with denominator greater than 1000:
| > | taylor(Int(t^2*exp(-t^2),t=0..x),x=0,15); |
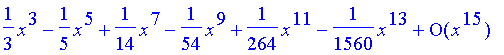
So going up through the ![]() term will do.
term will do.