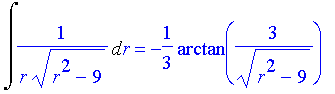
CHAPTER 7 - Techniques of Integration
Section 7.1, page560
Problem 32
| > | Int(1/(r*sqrt(r^2-9)),r)=int(1/(r*sqrt(r^2-9)),r); |
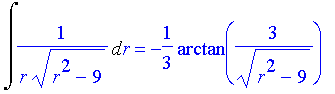
Problem 40
| > | Int(1/sqrt(2*theta-theta^2),theta)=int(1/sqrt(2*theta-theta^2),theta); |
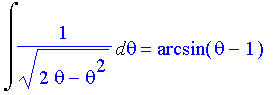
Problem 66
| > | Int(sqrt(1+cos(t)),t=-Pi..0)=int(sqrt(1+cos(t)),t=-Pi..0); |
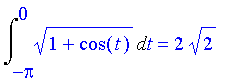
Section 7.2, page 567
Problem 14
| > | Int((r^2+r+1)*exp(r),r)=int((r^2+r+1)*exp(r),r); |
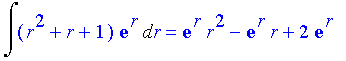
Problem 41
(a) Average value:
| > | avg:=simplify(1/(2*Pi-0)*int(2*exp(-t)*cos(t),t=0..2*Pi)); |
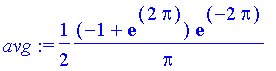
| > | plot({avg,2*exp(-t)*cos(t)},t=0..2*Pi,color=blue,thickness=2); |
![[Maple Plot]](images/m104-ex76.gif)
Section 7.3, page 576
Problem 11
We could just do the integral, but we want to point out that Maple can show you a partial fractions decomposition as follows:
| > | convert((x+4)/(x^2+5*x-6),parfrac,x); |
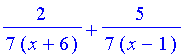
| > | Int((x+4)/(x^2+5*x-6),x)=int((x+4)/(x^2+5*x-6),x); |
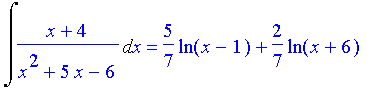
Problem 48
We'll find the centroid of the region. First, the area:
| > | f:=(4*x^2+13*x-9)/(x^3+2*x^2-3*x); |
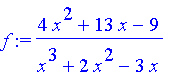
| > | area:=int(f,x=3..5); |
![]()
Now for the moments around the y and x axis:
| > | My:=int(x*f,x=3..5); |
![]()
| > | Mx:=int(f/2*f,x=3..5); |
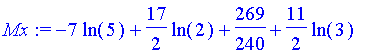
| > | centroid:=[My/area,Mx/area]; |
![centroid := [(8*ln(2)+8-3*ln(3))/(3*ln(5)-2*ln(3)), (-7*ln(5)+17/2*ln(2)+269/240+11/2*ln(3))/(3*ln(5)-2*ln(3))]](images/m104-ex713.gif)
| > | evalf(centroid); |
![]()
Section 7.4, page 582
Problem 24
| > | Int(sqrt(1-x^2)/x^4,x)=int(sqrt(1-x^2)/x^4,x); |
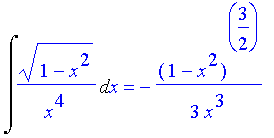
Section 7.6, page 603
Problem 21
| > | Int(theta*exp(theta),theta=-infinty..0)=int(theta*exp(theta),theta=-infinity..0); |
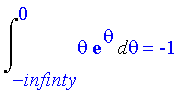
Problem 71
First graph the region that we are going to revolve around the y-axis:
| > | plot(exp(-x),x=0..10,color=blue,thickness=2); |
![[Maple Plot]](images/m104-ex717.gif)
We'll calculate the volume by shells -- for each x from 0 to infinity, the shell has radius x, thickness dx and height 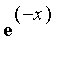 .
.
| > | volume:=int(2*Pi*x*exp(-x),x=0..infinity); |
![]()