CHAPTER 6 - Transcendental Functions
Section 6.1, page 454
Problem 31
We are given the function, and asked to find the derivative of its inverse at the point where
x=-1. We'll call the inverse function finv(x) We are also told (though we will solve for it here) that -1 = f(3). We'll start by writing the equation that defines the inverse function:
| > | eqn:=x=finv(x)^3-3*finv(x)^2-1; |
![]()
| > | rts:=solve(subs(x=-1,eqn),finv(-1)); |
![]()
Since we're only interested in values bigger than 2, we see that we should take finv(-1)=3. We could use the rule to calculate the derivative, but we'll just take the derivative of both sides of the equation:
| > | deqn:=diff(eqn,x); |
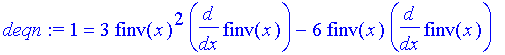
Now we'll solve this for the derivative of finv:
| > | solve(deqn,diff(finv(x),x)); |
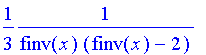
Finally, we'll substitute what we know: that finv(-1)=3. This will give us d finv/dx at x=-1.
| > | subs(finv(x)=3,%); |
![]()
Let's compare this with the "formula way" -- we should just take 1/y' evaluated at -1:
| > | 1/subs(x=3,diff(x^3-3*x^2-1,x)); |
![]()
(see the Math 103 solved problems for more from this section)
Section 6.2, page 465
Problem 82
To solve this second-order differential equation, we'll integrate twice (be sure to add the +C each time!):
| > | dy:=int(sec(x)^2,x)+C; |
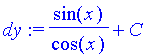
| > | y:=int(dy,x)+K; |
![]()
Now we'll apply the initial conditions: y(0)=0 and y'(0)=1:
| > | simplify(solve({subs(x=0,y)=0,subs(x=0,dy)=1},{C,K})); |
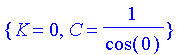
Well, we know that cos(0)=1 even if Maple doesn't seem to. So we put K=0, C=1 into y for the final answer:
| > | y:=subs(K=0,C=1,y); |
![]()
(see the Math 103 solved problems for more from this section)
Section 6.3, page 472
Problem 20
An easy one!
| > | diff(exp(4*sqrt(x)+x^2),x); |
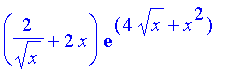
Problem 40
This is an implicit differentiation problem:
| > | restart; |
| > | eqn:=tan(y(x))=exp(x)+ln(x); |
![]()
| > | solve(diff(eqn,x),diff(y(x),x)); |
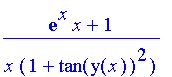
Problem 63
Another initial value problem. We'll solve this one using dsolve:
| > | dsolve({diff(y(t),t)=exp(t)*sin(exp(t)-2),y(ln(2))=0},y(t)); |
![]()
(see the Math 103 solved problems for more from this section)
Section 6.4, page 480
Problem 8
| > | solve(8^(log[8](3))-exp(ln(5))=x^2-7^(log[7](3*x)),x); |
![]()
Problem 27
| > | simplify(diff(log[2](r)*log[4](r),r)); |
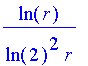
Problem 51
| > | Int(x*2^(x^2),x=1..sqrt(2))=int(x*2^(x^2),x=1..sqrt(2)); |
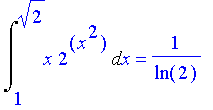
Problem 85
"Tangent line" idiom!
| > | f:=2^x; tanline:=subs(x=0,f)+subs(x=0,diff(f,x))*(x-0); |
![]()
![]()
| > | evalf(tanline); |
![]()
part (b)
| > | plot({f,tanline},x=-3..3,color=blue,thickness=2); |
![[Maple Plot]](images/m104-ex621.gif)
| > | plot({f,tanline},x=-1..1,color=blue,thickness=2); |
![[Maple Plot]](images/m104-ex622.gif)
Section 6.5, page 488
Problem 8
Exponential growth implies that:
| > | pop:=P*exp(k*t); |
![]()
The data we're given allow us to solve for k and P
| > | solve({subs(t=3,pop)=10000,subs(t=5,pop)=40000},{P,k}); |
![]()
Obviously only the first one of these makes sense. And P=1250 is the answer to our problem, since it asks for the number of bacteria present initially.
Problem 12
(a) The price p per unit ordered depends on the number x of units ordered according to the differential equation
| > | deqn:=diff(p(x),x)=-0.01*p(x); |
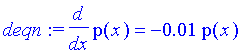
And we know that p(100)=20.09. So we have the initial condition
| > | init:=p(100)=20.09; |
![]()
We can apply dsolve to this:
| > | dsolve({deqn,init},p(x)); |
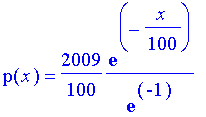
| > | p:=simplify(rhs(%)); |
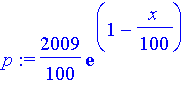
(b) Some sample prices: For 10 unit and 90 unit orders:
| > | evalf(subs(x=10,p)),evalf(subs(x=90,p)); |
![]()
(c),(d) Revenue = x*p -- we'll graph first, then find the max:
| > | rev:=x*p; plot(rev,x=0..120,color=blue,thickness=2); |
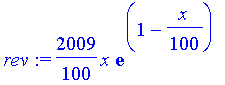
![[Maple Plot]](images/m104-ex631.gif)
| > | solve(diff(rev,x)=0,x); |
![]()
Section 6.6, page 496
Problem 35
(Maple knows limits):
| > | Limit(1/(x-1)-1/ln(x),x=1,right)=limit(1/(x-1)-1/ln(x),x=1,right); |
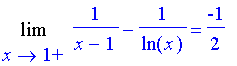
Problem 65
(a) First the verification:
| > | Limit((1+1/x)^x,x=infinity)=limit((1+1/x)^x,x=infinity); |
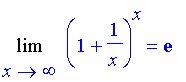
(b) We'll make a sequence of larger and larger x's and values of 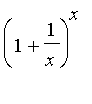 :
:
| > | f:=(1+1/x)^x; |
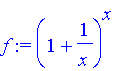
| > | seq([10^k,evalf(subs(x=10.0^k,f))],k=1..15); |
![]()
![]()
![]()
![]()
![]()
Something happened around 10^9 -- we fell victim to round-off error. To go farther, we can have Maple keep more decimal places as follows:
| > | Digits:=20; |
![]()
| > | seq([10^k,evalf(subs(x=10.0^k,f))],k=1..15); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | evalf(exp(1)); |
![]()
So we're getting pretty close. Let's try graphing, as suggested in the text:
| > | Digits:=10; |
![]()
| > | plot(f,x=1..10^10); |
![[Maple Plot]](images/m104-ex655.gif)
That looks good -- perhaps we can go farther:
| > | plot(f,x=10^10..10^12); |
![[Maple Plot]](images/m104-ex656.gif)
So we see the roundoff problem begin to emerge.
Section 6.7, page 503
Problem 8
We'll check this by taking limits of quotients:
| > | limit(2^x/x^2,x=infinity); |
![]()
| > | limit(ln(2)^x/2^x,x=infinity); |
![]()
| > | limit(ln(2)^x/x^2,x=infinity); |
![]()
| > | limit(exp(x)/2^x,x=infinity); |
![]()
So we have 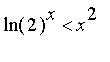 <
< 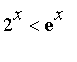 when x goes to infinity (in fact,
when x goes to infinity (in fact,
| > | limit(ln(2)^x,x=infinity); |
![]()
so it doesn't grow at all!)
Section 6.8, page 510
Problem 19
| > | simplify(tan(arcsin(-1/2))); |
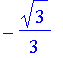
Problem 29
| > | simplify(sec(arctan(x/2))); |
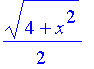
Problem 44
| > | Limit(arctan(x),x=-infinity)=limit(arctan(x),x=-infinity); |

Section 6.9, page 518
Problem 36
| > | Int(6/sqrt(4-(r+1)^2),r)=int(6/sqrt(4-(r-1)^2),r); |
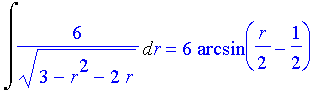
Problem 58
| > | Int(exp(arccos(x))/sqrt(1-x^2),x)=int(exp(arccos(x))/sqrt(1-x^2),x); |
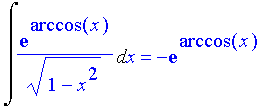
Section 6.11, page 537
Problem 10
We'll apply "dsolve"
| > | eqn:=(y(x)+1)*diff(y(x),x)=y(x)*(x-1); |
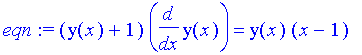
| > | dsolve(eqn,y(x)); |
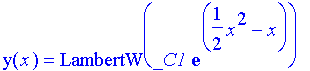
Maple has solved explicitly even though you might not have been able to. In fact, after separating, you'd get:
| > | int((y+1)/y,y)=int(x-1,x)+C; |
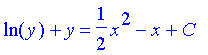
| > | solve(%,y); |
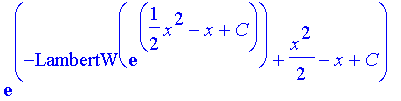
which differs from the dsolve solution by the definition of the constant.
Problem 16
| > | eqn:=exp(x)*diff(y(x),x)+2*exp(x)*y(x)=1; |
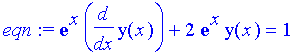
| > | dsolve(eqn,y(x)); |
![]()
Problem 40
An initial-value problem:
| > | eqn:=diff(y(x),x)+x*y(x)=x; init:=y(0)=-6; |
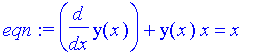
![]()
| > | dsolve({eqn,init},y(x)); |
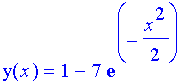
Problem 46
First set up and solve the initial-value problem:
| > | eqn:=diff(x(t),t)=1000+0.1*x(t); init:=x(0)=1000; |
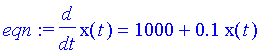
![]()
| > | dsolve({eqn,init},x(t)); |
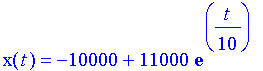
The question in part (b) is when will this equal 100000:
| > | solve(rhs(%)=100000,t); |
![]()
| > | evalf(%); |
![]()
So it takes about 23 years to get to $100,000.
Section 6.12, page 545
Problem 3
Maple has numerical DE solvers, but they are more sophisticated than Euler's method. If we really want to use Euler's method, we have to write it ourselves as follows: If the equation is y ' = f(x,y), then we'll define f first, then set
| > | eul:=(x,y,h)->y+h*f(x,y); |
![]()
This will give the next value of y. So for this problem we'd get:
| > | f:=(x,y)->2*x*y+2*y; |
![]()
| > | eul(0,3,0.2); |
![]()
So y(0)=3, and y(0.2)=4.2. Next,
| > | eul(0.2,4.2,0.2); |
![]()
| > | eul(0.4,%,0.2); |
![]()
And so forth. Our first four points are [0,3], [0.2,4.2], [0,4,6.216], [0.6,9.69696].
Problem 18
We use the DEplot command in the DEtools library (see the section in the manual on this command for more details):
| > | with(DEtools,DEplot): |
| > | DEplot(diff(y(x),x)=2*(y(x)-4),y(x),x=-2..2,y=-3..8,{[0,1],[0,4],[0,5]},thickness=2,color=blue,linecolor=black); |
![[Maple Plot]](images/m104-ex688.gif)