![[Maple Plot]](images/m104-ex121.gif)
CHAPTER 12 - Multivariable functions and partial derivatives
Section 12.1, page 914
Problem 25
First we'll do a 3D plot:
| > | plot3d(4*x^2+y^2,x=-3..3,y=-5..5,axes=boxed); |
![[Maple Plot]](images/m104-ex121.gif)
You get the idea, but if we display it with contours, it's better:
| > | plot3d(4*x^2+y^2,x=-3..3,y=-5..5,style=patchcontour,axes=boxed); |
![[Maple Plot]](images/m104-ex122.gif)
So you can guess what the contour plot will look like:
| > | with(plots,contourplot): |
| > | contourplot(4*x^2+y^2,x=-3..3,y=-4..4,scaling=constrained,contours=[1,2,3,4,5,6,7,8],grid=[80,80],color=blue,thickness=2); |
![[Maple Plot]](images/m104-ex123.gif)
Section 12.2, page 921
Problem 12
Maple doesn't do two-variable limits. We can do iterated limits, which give evidence for, but not proof of existence of a limit.
| > | limit(limit((cos(y)+1)/(y-sin(x)),x=Pi/2),y=0); |
![]()
| > | limit(limit((cos(y)+1)/(y-sin(x)),y=0),x=Pi/2); |
![]()
So the limit is (probably) -2.
Section 12.3, page 931
Problem 30
| > | f:=y*z*ln(x*y); |
![]()
| > | Diff(f,x)=diff(f,x); |
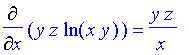
| > | Diff(f,y)=diff(f,y); |
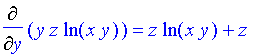
| > | Diff(f,z)=diff(f,z); |